Як довести що одна площина перпендикулярна інший. Перпендикулярні площині, умова перпендикулярності площин. Перпендикулярність в просторі можуть мати

Нагадаємо, що площині називаються перпендикулярними, якщо кут між ними прямий. А кут цей визначається так. Беруть точку О на прямій С, по якій перетинаються площини, і проводять через неї в площинах прямі (рис. 1.9а). Кутом між а і b і вимірюється кут між. Коли цей кут прямий, то кажуть, що площині взаємно перпендикулярні і пишуть

Ви, звичайно, вже помітили, що коли, то з трьох прямих а, b, з будь-які дві взаємно перпендикулярні (рис. 2.28). Зокрема, . Тому (за ознакою перпендикулярності прямої і площини). аналогічно,

Отже, кожна з двох взаємно перпендикулярних площин містить перпендикуляр до іншої площини. Більш того, ці перпендикуляри заповнюють взаємно перпендикулярні площини. (Рис. 2.29).

Доведемо останнє твердження. Дійсно, якщо через будь-яку точку площини а провести пряму

Те (по теоремі 5 про паралельність перпендикулярів).

А для ознаки перпендикулярності площин досить одного перпендикуляра до площини.

Теорема 7. (ознака перпендикулярності площин). Якщо площина проходить через перпендикуляр до іншої площини, то ці площини взаємно перпендикулярні.

Нехай площину а містить пряму а, перпендикулярну площині Р (рис. 2.28). Тоді пряма а перетинає площину Р в точці О. Крапка Про лежить прямий С, по якій перетинаються. Проведемо в площині Р через точку Про пряму. Так як і b лежить в площині Р, то Отже,

Даний ознака має простий практичний сенс: площину двері, навішеній на перпендикулярний підлозі косяк, перпендикулярна площині статі при будь-яких положеннях двері (рис. 2.1). Інша практичне застосування цієї ознаки: коли потрібно перевірити, чи вертикально встановлена \u200b\u200bплоска поверхня (стіна, паркан і т. П.), То це роблять за допомогою схилу - мотузки з вантажем. Схил завжди спрямований вертикально, і стіна стоїть вертикально, якщо в будь-якому її місці схил, розташовуючись уздовж неї, не відхиляється.

При вирішенні завдань, в яких зустрічаються перпендикулярні площині, часто використовуються наступні три пропозиції.

Пропозиція 1. Пряма, що лежить в одній з двох взаємно перпендикулярних площин і перпендикулярна їх загальної прямий, перпендикулярна іншій площині.

Нехай площині взаємно перпендикулярні і перетинаються по прямій С. Нехай, далі, пряма а лежить в площині а і (рис. 2.28). Пряма а перетинає пряму С в деякій точці О. Проведемо через точку О в площині Р пряму b, перпендикулярну прямий с. Так як то. Оскільки, то (по теоремі 2).

Друга пропозиція назад першому.

Пропозиція 2. Пряма, що має загальну точку з однією з двох взаємно перпендикулярних площин і перпендикулярна іншій площині, лежить в першій з них.

Нехай площині взаємно перпендикулярні, пряма а також пряма а має з площиною а загальну точку А (рис. 2.30). Через точку А в площині а проведемо пряму перпендикулярну прямий С - лінії перетину площин. Згідно з пропозицією Оскільки в просторі через кожну точку проходить лише одна пряма, перпендикулярна даній площині, то прямі а і збігаються. Так як лежить в площині а, то і а лежить в площині

Пропозиція 3. Якщо дві площини, перпендикулярні третьої площині, перетинаються, то пряма їх перетину перпендикулярна третьої площині.

Нехай дві площини, що перетинаються по прямій а, перпендикулярні площині у (рис. 2.31). Тоді через будь-яку точку прямої а проведемо пряму, перпендикулярну площині у. Згідно з пропозицією 2, ця пряма лежить і в площині а, і в площині Р, т. Е. Збігається з прямою а. Отже,

Ðассматрівается відношення перпендикулярності площин - одне з найважливіших і найбільш використовуваних в геометрії простору і її додатках.

З усього розмаїття взаємного розташування

двох площин на особливу увагу і вивчення заслуговує те, при якому площини перпендикулярні один одному (наприклад, площини суміжних стін кімнати,

забору та ділянки землі, двері і статі і т. п. (рис. 417, а-в).

Наведені приклади дозволяють побачити одне з основних властивостей відносини, яке ми будемо вивчати, - симетричність розташування кожної з площин відносно іншої. Симетрія забезпечується тим, що площині начебто «виткані» з перпендикулярів. Спробуємо уточнити ці спостереження.

Нехай маємо площину α і пряму з на ній (рис. 418, а). Проведемо через кожну точку прямойс прямі, перпендикулярні площині α. Всі ці прямі паралельні між собою (чому?) І складають, на підставі завдання 1 § 8, деяку площину β (рис. 418, б). Природно назвати площину β перпендикуляр ноїплощині α.

У свою чергу, всі прямі, що лежать в площині α і перпен- дікулярние прямойс, утворюють площину α і перпендикулярні площині β (рис. 418, в). Дійсно, есліа - довільна така пряма, то вона перетинає прямуюс в деяких точках. Через точкуМ проходить в площині β перпендикулярна α пря маяb, поетомуb а. Отже, а з, а b, поетомуа β. Таким чином, площина α перпендикулярна площині β, а пря Маясов є лінією їх перетину.

Дві площини називаються перпендикулярними, якщо кожна з них утворена прямими, перпенд кулярной другий площині і що проходять через точки перетину цих площин.

Перпендікулярностьплоскостейαіβобоз- почали звичним вже знаком: α β.

Одну з ілюстрацій цього визначення можна уявити, якщо розглянути фраг- мент кімнати дачного будиночка (рис. 419). У ньому підлогу і стіна складені з дощок, перпен- дікулярних соотвественно стіни і підлоги. По- цьому вони перпендикулярні. На практиці

це означає, що стать горизонтален, а стіна вертикальна.

Наведене визначення важко використовувати при фактичних кой перевірці перпендикулярності площин. Але якщо ува- тельно проаналізувати міркування, які привели до цього визначення, то бачимо, що перпендикулярність площин α і β забезпечило наявність в площині β прямойb, перпендикулярній площині α (рис. 418, в). Ми прийшли до ознакою перпендіку- лярность двох площин, який найчастіше застосовується на практиці.

406 Перпендикулярність прямих і площин

Теорема 1 (ознака перпендикулярності площин).

Якщо одна з двох площин проходить через пряму, перпендикулярну другий площині, то ці площини перпендикулярні.

 Нехай площину β проходить через прямуюb, перпендикулярні до площини α ис - лінія перетину площин α і β (рис. 420, а). Всі прямі площині β, паралельні прямойb і перетинають прямуюс, разом з прямойb утворюють площину β. По теоремі про двох паралельних прямих, одна з яких пер пендікулярна площині (теорема 1 § 19), всі вони разом з прямойb перпендикулярні площині α. Тобто площину β складається з прямих, що проходять через лінію перетину площин α і β і перпендикулярних площині α (рис. 420, б).

Тепер в площині α через точку А перетину прямихb ис проведемо прямуюа, перпендикулярну прямойс (рис. 420, в). Прямаяа перпендикулярна площині β, за ознакою перпен- дікулярності прямої і площини (а з, з побудови, а b, так какb α). Повторивши попередні міркування, отримаємо, що площина α складається з прямих, перпендикулярних площині β, що проходять через лінію перетину площин. Згідно оп- ределению, площини α і β перпендикулярні. ■

Наведений ознака дає можливість встановлювати пер- пендікулярность площин або ж забезпечувати її.

П р и м і р 1. Прикріпити щит до стовпа так, щоб він був распо- хибна вертикально.

 Якщо стовп стоїть вертикально, то досить прикласти довільно щит до стовпа і закріпити його (рис. 421, а). Згідно розглянутому вище ознакою, площина щита буде перпенді- кулярной поверхні землі. У цьому випадку завдання має беско- кінцевого безліч рішень.

Якщо ж стовп стоїть похило до землі, то досить до стовпа прикріпити вертикальну рейку (рис. 421, б), а потім щит прикріпити і до рейки, і до стовпа. У цьому випадку положення щита бу- дет цілком певним, оскільки стовп і рейка визначають єдину площину. ■

У попередньому прикладі «технічне» завдання звелося до мате- тичних задачі про проведення через дану пряму площині, перпендикулярній іншій площині.

П р и м і р 2. З вершіниA квадратаABCD проведено перпен- дікулярний його площині отрезокAK, AB \u003d AK \u003d а.

1) Визначити взаємне розташування площин AKC іABD,

AKD і ABK.

2) Побудувати площину, що проходить через пряму BD перпенді- кулярной плоскостіABC.

3) Провести через середину F отрезкаKC площину, перпендикулярні до плоскостіKAC.

4) Знайти площу трикутника BDF.

 Побудуємо малюнок, відповідний умовою прикладу (рис. 422).

1) Площини AKC іABD перпендикулярно ни, за ознакою перпендикулярності плос- кісток (теорема 1): AK ABD, за умовою. ПлоскостіAKD іABK також перпендіку-

лярні, за ознакою перпендикулярності площин (теорема 1). Дійсно, прямаяAB, через кото рую проходить плоскостьABK, перпендикулярна плоскостіAKD, за ознакою перпендикулярності прямої і площини (теорема 1 § 18): АВ AD, як суміжні сторони квадрата; АВ AK, так як

AK ABD.

2) За ознакою перпендикулярності площин, для шуканого построеніядостаточночерезнекоторуюточкупрямойBD провести

408 Перпендикулярність прямих і площин

пряму, перпендикулярну площині ABC. А для цього достатньою але через цю точку провести пряму, паралельну прямойAK.

Дійсно, за умовою, пряма AK перпендикулярна плос- костіABC і тому, відповідно до теореми про двох паралельних пря

Теорема 2 (про перпендикуляр до лінії перетину перпенді- кулярной площин).

Якщо дві площини перпендикулярні, то пряма, яка належить одній площині і перпендикулярна лінії перетину цих площин, перпендикулярна другий площині.

 Нехай перпендикулярні площині

α і β перетинаються по прямій с, а прямаяb в площині β перпендикулярна прямойс і перетинає її в точці (рис. 425). за ви-

поділу перпендикулярності площин, в площині β через точку В проходить пряма

b 1, перпендикулярна площині α. Зрозуміло, що вона перпендикулярна прямойс. але че-

рез точку прямої в площині можна провес- ти лише одну пряму, перпендикулярну даної прямий. Тому

прямі b і b 1 збігаються. А це означає, що пряма одній площині, перпендикулярна лінії перетину двох перпендикулярних площин, перпендикулярна другий площині. ■

Застосуємо розглянуту теорему до обгрунтування ще однієї ознаки перпендикулярності площин, важливого з точки зре- ня подальшого вивчення взаємного розташування двох площин.

Пустьплоскостіαіβперпендікулярни, пряма с - лінія їх перетину. Через довільну точкуА прямойс проведемо

в площинах α і β прямі а і b, перпен- дікулярние прямойс (рис. 426). за теоре-

ме 2, прямі а і b перпендикулярні від- повідно площинах β і α, тому вони перпендикулярні між собою: а b. пря

мие а иb визначають деяку площину γ. Лінія пересеченіяс площин α і β

перпендикулярна площині γ, за ознакою перпендикулярності прямої і площини (теорема 1 § 18): з а, з b, а γ, b γ. Якщо врахувати довільність вибору точки на прямойс і той факт, що через точкуА прямойс проходить єдина площина, їй перпендикулярна, то можна зробити наступний висновок.

Теорема 3 (про площині, перпендикулярній лінії пере- ня перпендикулярних площин).

Площина, перпендикулярна лінії перетину двох перпендикулярних площин, перетинає ці площини по перпендикулярним прямим.

Таким чином, встановлено ще одну властивість перпендіку- лярних площин. Ця властивість є характеристичним, тобто якщо воно справедливо для деяких двох площин, то площини перпендикулярні між собою. Маємо ще один при- знак перпендикулярності площин.

Теорема 4 (друга ознака перпендикулярності плоскос- тей).

Якщо прямі перетину двох площин третьою площиною, перпендикулярної лінії їх перетину, перпендикулярні, то дані площині теж перпендикулярні.

 Нехай площині α і β перетинаються по прямойс, і площину γ, перпендикулярна прямойс, перетинає площині α і β від-

повідно за прямими а і b (рис. 427). За умовою, а b. Оскільки γс, тоа с. А тому прямаяа перпендикулярна площині β, за ознакою перпендикулярності прямої і площини (теорема 1 § 18). Отсю-

да випливає, що площині α і β перпенді- кулярной, за ознакою перпендікулярнос- ти площин (теорема 1). ■

Заслуговують на увагу і теореми про зв'язки перпендикулярно ності двох площин третьою площині з їх взаємним распо- становищем.

Теорема 5 (про лінії перетину двох площин, перпендикулярні до третьої площини).

Якщо дві площини, перпендикулярні третьої площині, перетинаються, то лінія їх перетину перпендикулярна цій площині.

 Нехай площині α і β, перпендикулярні площині γ, пере- Сека по прямойа (a || γ), ІА - точка перетину прямойа з

Розглянемо теорему, яка описує зв'язок між паралель- ністю і перпендикулярністю площин. Відповідний ре- зультат ми вже мали для прямих і площин.

Теорема 6 (про паралельних площинах, перпендикулярних третьої площині).

Якщо одна з двох паралельних площин перпендикулярна третій, то і друга площина перпендикулярна їй.

 Нехай площині α і β паралельних, а площину γ перпендикулярно на площині α. Оскільки площину γ

перетинає площину α, то вона повинна перетинати і паралельну їй площину β. Візьмемо в площині α про-

довільно пряму m, перпендикулярні до площини γ, і проведемо через неї, а також через довільну точ- ку площині β, площину δ (рис. 429).

Площині δ і β перетинаються по прямій п, а оскільки α║ β, той ║ п (теорема 2 §18). З теореми 1 випливає, чтоп γ, а тому перпендикулярній площині γ буде і площину β, що проходить через прямуюп. ■

Доведена теорема дає ще одна ознака перпендикулярно ності площин.

Через задану точку провести площину, перпендикулярну даної, можна за допомогою ознаки перпендикулярності плоскос- тей (теорема 1). Досить через цю точку провести пряму, пер пендікулярную цій площині (див. Задачу 1 § 19). А потім через построеннуюпрямуюпровестіплоскость.Онабудетперпендікуляр- ної цій площині за вказаною ознакою. Зрозуміло, що таких площин можна провести безліч.

Більш змістовною є завдання про побудову плоскос- ти, перпендикулярної даній, за умови, що вона проходить че- рез дану пряму. Зрозуміло, що якщо дана пряма перпенді- кулярной цій площині, то таких площин можна побудувати безліч. Залишилося розглянути випадок, коли дан ная прямо не перпендикулярна даній площині. Можливість такого побудови обгрунтована на рівні фізичних моделей прямих і площин в прикладі 1.

З а д а ч а 1. Довести, що через довільну пряму, що не пер- пендікулярную площині, можна провести площину, перпенді- кулярную цій площині.

 Нехай дано площину α і прямаяl, l B \\ a. Візьмемо на прямойl довільну точкуМ і проведемо через неї пряму, перпен- дікулярную площині α (рис. 430, а). Оскільки, за умовою, l НЕ перпендикулярна α, то прямиеl ит перетинаються. Через ці прямі можна провести площину β (рис. 430, б), яка, соглас- але ознакою перпендикулярності площин (теорема 1), буде перпендикулярної площині α. ■

П р и м і р 3. Через вершінуА правильної пірамідиSABC з основаніемABC провести пряму, перпендикулярну площині бічній граніSBC.

 Для вирішення даного завдання скористаємося теоремою про пер- пендікуляре до лінії перетину перпендикулярних площин

(Теорема 2). Нехай K - середина ребраBC (рис. 431). ПлоскостіAKS іBCS перпенді- кулярной, за ознакою перпендікулярнос- ти площин (теорема 1). Дійсно, ВС SK ІТТ Аk, як медіани, проведено- ні до підстав в рівнобедрених тре косинцях. Тому, за ознакою перпенді- кулярной прямої і площини (теорема 1 §18), прямаяВС перпендикулярна плоскостіAKS. ПлоскостьBCS проходить через пряму, перпендикулярну плоскостіAKS.

Побудова. Проведемо в плоскостіAKS з точкіA прямуюAL, перпендикулярну прямойKS - лінії перетину плоскостейAKS іBCS (рис. 432). По теоремі про перпен- дікуляре до лінії перетину перпендіку- лярних площин (теорема 2), прямаяAL перпендикулярна плоскостіBCS. ■

2. На рис. 434 зображена правиль- ная чотирикутна піраміда

SABCD, точки P, M, N -середі -

ни ребер AB, BC, BS, O-центр підстави ABCD. Які з пар пло- кісток перпендикулярні:

1) ACS і BDS; 2) MOSі POS;

3) COS і MNP; 4) MNPі SOB;

5) CND і ABS?

3) PACі PBC; 4) PACі PAB?

4. Дві площини перпендикулярні. Чи можна через довільну точку однією зних провести пряму в цій площині, другий площині?

5. В площині α можна провести пряму, площини β. Чи можуть ці площини бути ми?

6. Через деяку точку площини α проходить щая в цій площині і перпендикулярна площині чи, що площині α і β перпендикулярні?

Секція огорожі прикріплена до вертикального стовпа Чи можна стверджувати, що площину забору вертикальна?

Як до рейки, паралельній поверхні землі, прикріпити вертикально щит?

Чому поверхню дверей, незалежно від того, закриті вони чи відкриті, розташовується вертикально до підлоги?

Чому схил щільно прилягає до вертикальної стіни, а до на- клон - не обов'язково?

Чи можна до похилого стовпа прикріпити щит так, щоб він був перпендикулярний поверхні землі?

Як на практиці встановити, перпендикулярна чи площину

стіни площині статі? перпендікулярнуюперпендікулярнуюперпендікулярни- пряма, лежачи - β. Вірно 7.. Можна 8.9.10.11.12.

графічні вправи

1. На рис. 436 зображений кубABCDA 1 B 1 C 1 D 1.

1) Вкажіть площині, перпендикулярні площиніВDD 1.

2) Як розташовані площині і

A1 B1 CAB 1 C 1

421. ОтрезокOS проведено з Централ квадратаABCD перпен- дікулярно його площині.

1 °) Визначте взаємне розташування площин ACS

і АВС.

2 °) Визначте взаємне розташування площин ACS

і BDS.

3) Побудуйте площину, що проходить через пряму OS пер- пендікулярно плоскостіABS.

4) Побудуйте площину, перпендикулярну площині АВС і проходить через середини сторонAD іCD.

422. З точки пересеченіяO діагоналей ромбаABCD проведено перпендикулярний площині ромба отрезокOS; AB \u003d DB \u003d

1 °) Визначте взаємне розташування площин SDB і

ABC, SDBі ACS.

2 °) Побудуйте площину, що проходить через пряму BC пер- пендікулярно плоскостіABD.

3) Проведіть через середину F отрезкаCS площину, пер пендікулярную плоскостіАВС.

4) Знайдіть площу трикутника BDF.

423. Дан куб ABCDA1 B1 C1 D1.

1 °) Визначте взаємне розташування площин АВ 1 З 1

і CDD1.

2 °) Визначте взаємне розташування площин АВ 1 З 1

і CD1 A1.

3 °) Побудуйте площину, що проходить через точку А перпен- дікулярно плоскостіBB 1 D 1.

4) Побудуйте переріз куба площиною, що проходить через се Редіна ребер 1 D 1 і b 1 C 1 перпендикулярно плоскостіАВС. 5) ОпределітевзаімноерасположеніеплоскостіАА 1 В іплос- кістки, що проходить через середини ребер 1 В 1, C 1 D 1, CD.

6) Знайдіть площу перерізу куба площиною, що проходить через ребро ВВ 1 і середину ребраA 1 D 1 (ВВ 1 \u003d а).

7) Побудуйте точку, симетричну точці А відносно плоскостіA 1 B 1 C.

424. В правильному тетраедреАBCD з ребром 2 см точки - се редінаDВ, а точкаN - середінаАС.

1 °) Доведіть, що пряма D В перпендикулярна площині

2 °) Доведіть, що площина ВDМ перпендикулярна плос- костіАМС.

3) Через точку Про перетину медіан треугольнікаАDС проведіть пряму, перпендикулярну плоскостіАМС.

4) Знайдіть довжину відрізка цієї прямої всередині тетраедра. 5) У якому відношенні площина АМС ділить цей відрізок?

425. Два рівносторонніх треугольнікаАВС іADC лежать в пер- пендікулярних площинах.

1 °) Знайдіть довжину відрізка BD, есліAC \u003d 1 см.

2) Доведіть, що площина BKD (K лежить на прямойAC) перпендикулярна площині кожного з трикутників тоді і тільки тоді, когдаK є серединою сторониAC.

426. ПрямоугольнікABCD, сторони якого 3 см і 4 см, пере- гнули по діагоналіAC так, що треугольнікіABC іADC розташувалися в перпендикулярних площинах. Визна літі відстань між точкаміB иd після того, як пере- гнули прямоугольнікABCD.

427. Через дану точку проведіть площину, перпендикулярно ву кожної з двох даних площин.

428 °. Доведіть, що площині суміжних граней куба перпендикулярні.

429. Площини α і β перпендикулярні між собою. З точки площині α проведена перпендикулярна площині β пря маяАВ. Доведіть, що прямаяАВ лежить в площині α.

430. Доведіть, що якщо площина і пряма, що не лежить у цій площині, перпендикулярні одній і тій же площині, то вони паралельні між собою.

431. Через точку верб, що лежать на лінії пересеченіяр пер- пендікулярних між собою площин α і β, проведені перпендікулярниер прямі: АА 1 в α, ВВ 1 в β. ТочкаX ле- жит на прямойАА 1, а точкаY - наВB 1. Доведіть, що пря- маяВB 1 перпендикулярна прямойВХ, а прямаяАA 1 перпендикулярна прямойАY.

432 *. Через середину кожної сторони трикутника проведена площина, перпендикулярна цій стороні. Доведіть, що всі три проведені площині перетинаються по одній пря мій, перпендикулярній площині трикутника.

Вправи для повторення

433. У рівносторонньому трикутнику зі стороноюb визначте: 1) висоту; 2) радіуси вписаного та описаного кіл.

434. З однієї точки проведено до даної прямої перпендикуляр і дві похилі. Визначте довжину перпендикуляра, якщо похилі рівні 41 см і 50 см, а їх проекції на дану пряму відносяться, як 3: 10.

435. Визначте катети прямокутного трикутника, Якщо біс- сектріса прямого кута ділить гіпотенузу на відрізки 15 см і

Основне визначення

Дві площини називаючи-

ються перпендикуляр ними , Якщо кожна з них утворена прямі- ми, перпендикулярні- мі другої площини і проходять через точки перетину цих площин.

Поняття перпендикулярних площин

При перетині двох площин у нас виходить $ 4 $ двогранні кута. Два кути рівні $ \\ varphi $, а два інші рівні $ (180) ^ 0- \\ varphi $.

визначення 1

Кутом між площинами називається мінімальний з двогранні кутів, утворених цими площинами.

визначення 2

Дві пересічні площині називаються перпендикулярними, якщо кут між цими площинами дорівнює $ 90 ^ \\ circ $ (рис. 1).

Малюнок 1. перпендикулярні площині

Ознака перпендикулярності двох площин

теорема 1

Якщо пряма площині перпендикулярна іншій площині, то ці площини перпендикулярні один одному.

Доведення.

Нехай нам дано площині $ \\ alpha $ і $ \\ beta $, які перетинаються по прямій $ AC $. Нехай пряма $ AB $, що лежить в площині $ \\ alpha $ перпендикулярна площині $ \\ beta $ (рис. 2).

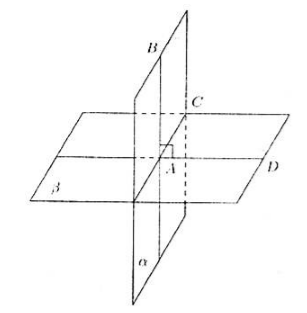
Малюнок 2.

Так як пряма $ AB $ перпендикулярна площині $ \\ beta $, то вона перпендикулярна і прямий $ AC $. Проведемо додатково пряму $ AD $ в площині $ \\ beta $, перпендикулярно прямий $ AC $.

Отримуємо, що кут $ BAD $ - лінійний кут двогранного кута, що дорівнює $ 90 ^ \\ circ $. Тобто, за визначенням 1, кут між площинами дорівнює $ 90 ^ \\ circ $, значить, дані площини перпендикулярні.

Теорема доведена.

З цієї теореми випливає наступна теорема.

теорема 2

Якщо площина перпендикулярна прямий, по якій перетинаються дві інші площини, то вона перпендикулярна і цим площинах.

Доведення.

Нехай нам дано дві площини $ \\ alpha $ і $ \\ beta $, пересічні по прямій $ c $. Площина $ \\ gamma $ перпендикулярна прямий $ c $ (рис. 3)

Малюнок 3.

Так як пряма $ c $ належить площині $ \\ alpha $ і площину $ \\ gamma $ перпендикулярна прямий $ c $, то, по теоремі 1, площині $ \\ alpha $ і $ \\ gamma $ перпендикулярні.

Так як пряма $ c $ належить площині $ \\ beta $ і площину $ \\ gamma $ перпендикулярна прямий $ c $, то, по теоремі 1, площині $ \\ beta $ і $ \\ gamma $ перпендикулярні.

Теорема доведена.

Для кожної з цих теорем справедливі і зворотні твердження.

приклади завдань

приклад 1

Нехай нам дано прямокутний паралелепіпед $ ABCDA_1B_1C_1D_1 $. Знайти всі пари перпендикулярних площин (рис. 5).

Малюнок 4.

Рішення.

За визначенням прямокутного паралелепіпеда і перпендикулярних площин бачимо наступні вісім пар перпендикулярних між собою площин: $ (ABB_1) $ і $ (ADD_1) $, $ (ABB_1) $ і $ (A_1B_1C_1) $, $ (ABB_1) $ і $ (BCC_1) $, $ ( ABB_1) $ і $ (ABC) $, $ (DCC_1) $ і $ (ADD_1) $, $ (DCC_1) $ і $ (A_1B_1C_1) $, $ (DCC_1) $ і $ (BCC_1) $, $ (DCC_1) $ і $ (ABC) $.

приклад 2

Нехай нам дано дві взаємно перпендикулярні площини. З точки однієї площини проведено перпендикуляр до іншої площини. Довести, що ця пряма лежить у цій площині.

Доведення.

Нехай нам дано перпендикулярні площині $ \\ alpha $ і $ \\ beta $, пересічні по прямій $ c $. З точки $ A $ площині $ \\ beta $ проведено перпендикуляр $ AC $ до площини $ \\ alpha $. Припустимо, що $ AC $ не лежить в площині $ \\ beta $ (рис. 6).

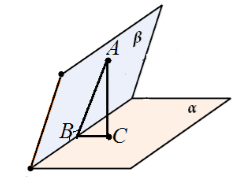
Малюнок 5.

Розглянемо трикутник $ ABC $. Він є прямокутним з прямим кутом $ ACB $. Отже, $ \\ angle ABC \\ ne (90) ^ 0 $.

Але, з іншого боку, $ \\ angle ABC $ є лінійним кутом двогранного кута, утвореного цими площинами. Тобто двогранний кут, утворений цими площини не дорівнює 90 градусам. Отримуємо, що кут між площинами НЕ дорівнює $ 90 ^ \\ circ $. Протиріччя. Отже, $ AC $ лежить в площині $ \\ beta $.

Даний урок допоможе бажаючим отримати уявлення про тему «Ознака перпендикулярності двох площин». На початку нього ми повторимо визначення двогранного і лінійного кута. Потім розглянемо, які площині називаються перпендикулярними, і доведемо ознака перпендикулярності двох площин.

Тема: Перпендикулярність прямих і площин

Урок: Ознака перпендикулярності двох площин

Визначення. Двогранним кутом називається фігура, утворена двома півплощини, що не належать одній площині, і їх загальної прямої а (а - ребро).

Мал. 1

Розглянемо дві півплощини α і β (рис. 1). Їх спільний кордон - l. Зазначена фігура називається двогранним кутом. Дві пересічні площині утворюють чотири двогранні кута із загальним ребром.

Двогранний кут вимірюється своїм лінійним кутом. На загальному ребрі l двогранного кута виберемо довільну точку. У півплощинах α і β з цієї точки проведемо перпендикуляри a і b до прямої l і отримаємо лінійний кут двогранного кута.

Прямі a і b утворюють чотири кути, рівних φ, 180 ° - φ, φ, 180 ° - φ. Нагадаємо, кутом між прямими називається найменший з цих кутів.

Визначення. Кутом між площинами називається найменший з двогранні кутів, утворених цими площинами. φ - кут між площинами α і β, якщо

Визначення. Дві пересічні площині називаються перпендикулярними (взаємно перпендикулярними), якщо кут між ними дорівнює 90 °.

Мал. 2

На ребрі l обрана довільна точка М (рис. 2). Проведемо дві перпендикулярні прямі МА \u003d а і МВ \u003d b до ребру l в площині α і в площині β відповідно. Отримали кут АМВ. Кут АМВ - це лінійний кут двогранного кута. Якщо кут АМВ дорівнює 90 °, то площини α і β називаються перпендикулярними.

Пряма b перпендикулярна прямий l з побудови. Пряма b перпендикулярна прямий а, так як кут між площинами α і β дорівнює 90 °. Отримуємо, що пряма b перпендикулярна двом пересічним прямим а і l з площини α. Значить, пряма b перпендикулярна площині α.

Аналогічно можна довести, що пряма а перпендикулярна площині β. Пряма а перпендикулярна прямий l з побудови. Пряма а перпендикулярна прямий b, так як кут між площинами α і β дорівнює 90 °. Отримуємо, що пряма а перпендикулярна двом пересічним прямим b і l з площини β. Значить, пряма а перпендикулярна площині β.

Якщо одна з двох площин проходить через пряму, перпендикулярну до іншій площині, то такі площини перпендикулярні.

довести:

Мал. 3

Доведення:

Нехай площині α і β перетинаються по прямій АС (рис. 3). Щоб довести, що площини взаємно перпендикулярні, потрібно побудувати лінійний кут між ними і показати, що цей кут дорівнює 90 °.

Пряма АВ перпендикулярна за умовою площині β, а значить, і прямий АС, що лежить в площині β.

Проведемо пряму АD перпендикулярно прямий АС в площині β. Тоді ВАD -Лінійний кут двогранного кута.

Пряма АВ перпендикулярна площині β, а значить, і прямий АD, що лежить в площині β. Значить, лінійний кут ВАD дорівнює 90 °. Значить, площини α і β перпендикулярні, що й треба було довести.

Площина, перпендикулярна до прямої, по якій перетинаються дві дані площини, перпендикулярна до кожної з цих площин (рис. 4).

довести:

Мал. 4

Доведення:

Пряма l перпендикулярна площині γ, а площину α проходить через пряму l. Значить, за ознакою перпендикулярності площин, площини α і γ перпендикулярні.

Пряма l перпендикулярна площині γ, а площину β проходить через пряму l. Значить, за ознакою перпендикулярності площин, площині β і γ перпендикулярні.