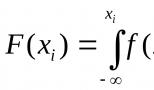l භාවිතය. විස්තාරය-අදියර ලක්ෂණය (Nyquist hodograph) L.A.Ch භාවිතය. සහ පද්ධති ස්ථාවරත්වය විශ්ලේෂණය කිරීම සඳහා අදියර සංඛ්යාත ලක්ෂණ
සංඛ්යාතය -∞ සිට +∞ දක්වා වෙනස් වන විට සංඛ්යාත හුවමාරු ශ්රිතයේ දෛශිකයේ අවසානය විස්තර කරන ලක්ෂ්යවල පිහිටීම මෙයයි. hodograph හි මූලාරම්භයේ සිට එක් එක් ලක්ෂ්යය දක්වා වූ කොටසෙහි ප්රමාණය, ලබා දී ඇති සංඛ්යාතයක දී ප්රතිදාන සංඥාව ආදාන සංඥාවට වඩා කොපමණ වාර ගණනක් වැඩි දැයි පෙන්වයි, සහ සංඥා අතර අදියර මාරුව තීරණය වන්නේ සඳහන් කළ කොටසට ඇති කෝණය අනුව ය.
අනෙකුත් සියලුම සංඛ්යාත පරායත්තතා AFC වෙතින් ජනනය වේ:
- යූ(w) - පවා (සංවෘත ස්වයංක්රීය පාලන පද්ධති සඳහා පී(w));
- වී(w) - ඔත්තේ;
- ඒ(w) - ඉරට්ටේ (සංඛ්යාත ප්රතිචාරය);
- j(w) - ඔත්තේ (අදියර ප්රතිචාරය);
- LACHH & LFCH - බොහෝ විට භාවිතා වේ.
ලඝුගණක සංඛ්යාත ලක්ෂණ.
ලඝුගණක සංඛ්යාත ලක්ෂණ (LFC) අතරට ලඝුගණක විස්තාරය ලක්ෂණයක් (LAFC) සහ ලඝුගණක අවධි ලක්ෂණයක් (LPFC) එක් තලයක වෙන වෙනම ඉදිකර ඇත. LFC සහ LFCH ඉදිකිරීම පහත ප්රකාශන භාවිතයෙන් සිදු කෙරේ:
එල්(w) = 20 lg | ඩබ්ලිව්(j w)| = 20 lg ඒ(w), [dB];
j(w) = arg( ඩබ්ලිව්(j w)), [rad].
විශාලත්වය එල්(w) තුළ ප්රකාශ වේ ඩෙසිබල් . බෙල්බලයේ දස ගුණයක වැඩිවීමකට අනුරූප වන ලඝුගණක ඒකකයකි. එක් බෙල් බලය 10 ගුණයකින් වැඩි කිරීමට අනුරූප වේ, 2 බෙල් - 100 ගුණයකින්, 3 බෙල් - 1000 ගුණයකින්, ආදිය. ඩෙසිබල් එකක් බෙල් එකකින් දහයෙන් එකකට සමාන වේ.
සාමාන්ය ගතික සබැඳි සඳහා AFC, AFC, PFC, LFC සහ LPFC හි උදාහරණ වගුව 2 හි දක්වා ඇත.
වගුව 2.සාමාන්ය ගතික සබැඳි වල සංඛ්යාත ලක්ෂණ.



ස්වයංක්රීය නියාමනය පිළිබඳ මූලධර්ම
පාලන මූලධර්මය මත පදනම්ව, ස්වයං චලිත තුවක්කු කණ්ඩායම් තුනකට බෙදිය හැකිය:
- බාහිර බලපෑම් මත පදනම් වූ නියාමනය සමඟ - Poncelet මූලධර්මය (විවෘත-ලූප් ස්වයං-ප්රචලිත තුවක්කු වල භාවිතා වේ).
- අපගමනය මගින් නියාමනය සමඟ - Polzunov-Watt මූලධර්මය (සංවෘත ස්වයං-ප්රචලිත තුවක්කු වල භාවිතා වේ).
- ඒකාබද්ධ නියාමනය සමඟ. මෙම අවස්ථාවේදී, ACS සංවෘත සහ විවෘත පාලන ලූප අඩංගු වේ.
බාහිර බාධා කිරීම් මත පදනම් වූ පාලන මූලධර්මය
 ව්යුහයට බාධා සංවේදක අවශ්ය වේ. පද්ධතිය විවෘත-ලූප් මාරු කිරීමේ කාර්යය මගින් විස්තර කෙරේ: x(ටී) = g(ටී) - f(ටී).
ව්යුහයට බාධා සංවේදක අවශ්ය වේ. පද්ධතිය විවෘත-ලූප් මාරු කිරීමේ කාර්යය මගින් විස්තර කෙරේ: x(ටී) = g(ටී) - f(ටී).
වාසි:
- යම් යම් කැළඹීම් සඳහා සම්පූර්ණ අස්ථාවරත්වය ලබා ගත හැකිය.
- පද්ධතියේ ස්ථායීතාවය පිළිබඳ ගැටළුව පැනනගින්නේ නැත, මන්ද OS නැත.
අඩුපාඩු:
- කැළඹීම් විශාල සංඛ්යාවක් සඳහා වන්දි නාලිකා අනුරූප සංඛ්යාවක් අවශ්ය වේ.
- පාලිත වස්තුවේ පරාමිතීන්හි වෙනස්කම් පාලනය කිරීමේදී දෝෂ ඇතිවේ.
- ලක්ෂණ පැහැදිලිව දන්නා වස්තූන් සඳහා පමණක් යෙදිය හැකිය.
අපගමනය පාලන මූලධර්මය
 පද්ධතිය විවෘත-ලූප් මාරු කිරීමේ කාර්යය සහ වසා දැමීමේ සමීකරණය මගින් විස්තර කෙරේ: x(ටී) = g(ටී) - y(ටී) ඩබ්ලිව් oc( ටී) පද්ධතියේ ඇල්ගොරිතම දෝෂය අඩු කිරීමට ඇති ආශාව මත පදනම් වේ x(ටී) බිංදුවට.
පද්ධතිය විවෘත-ලූප් මාරු කිරීමේ කාර්යය සහ වසා දැමීමේ සමීකරණය මගින් විස්තර කෙරේ: x(ටී) = g(ටී) - y(ටී) ඩබ්ලිව් oc( ටී) පද්ධතියේ ඇල්ගොරිතම දෝෂය අඩු කිරීමට ඇති ආශාව මත පදනම් වේ x(ටී) බිංදුවට.
වාසි:
- OOS දෝෂය අඩු කිරීමට හේතු වේ, එයට හේතු වූ සාධක නොසලකා (පාලිත වස්තුවේ පරාමිතීන් හෝ බාහිර තත්වයන් වෙනස් වේ).
අඩුපාඩු:
- OS පද්ධතිවල, ස්ථාවරත්වය පිළිබඳ ගැටළුවක් පවතී.
- පද්ධතිවල කැළඹීම් සඳහා නිරපේක්ෂ අස්ථාවරත්වය ලබා ගැනීම මූලික වශයෙන් කළ නොහැක්කකි. අර්ධ විචලනය ලබා ගැනීමට ඇති ආශාව (පළමු මෙහෙයුම් පද්ධතිය සමඟ නොවේ) පද්ධතියේ සංකූලතා සහ ස්ථාවරත්වය පිරිහීමට හේතු වේ.
 ඒකාබද්ධ පාලනය
ඒකාබද්ධ පාලනය
ඒකාබද්ධ පාලනය සමන්විත වන්නේ අපගමනය සහ බාහිර බාධා කිරීම් මත පදනම් වූ පාලන මූලධර්ම දෙකක එකතුවකිනි. එම. වස්තුවට පාලන සංඥාව නාලිකා දෙකක් මගින් ජනනය වේ. පළමු නාලිකාව ඉලක්කයෙන් පාලිත විචල්යයේ අපගමනයට සංවේදී වේ. දෙවැන්න ප්රධාන හෝ බාධාකාරී සංඥාවකින් සෘජුවම පාලන ක්රියාවක් ජනනය කරයි.
x(ටී) = g(ටී) - f(ටී) - y(ටී)Woc(ටී)
වාසි:
- OOS තිබීම පාලනය කරන ලද වස්තුවේ පරාමිතීන්හි වෙනස්කම් වලට පද්ධතිය අඩු සංවේදී කරයි.
- යොමු-සංවේදී හෝ බාධා-සංවේදී නාලිකාව(ය) එකතු කිරීම ප්රතිපෝෂණ ලූපයේ ස්ථායීතාවයට බලපාන්නේ නැත.
අඩුපාඩු:
- කාර්යයකට හෝ බාධාවකට සංවේදී වන නාලිකා සාමාන්යයෙන් එකිනෙකට වෙනස් සබැඳි අඩංගු වේ. ඒවා ප්රායෝගිකව ක්රියාත්මක කිරීම දුෂ්කර ය.
- සියලුම වස්තූන් බල කිරීමට ඉඩ නොදේ.
ATS ස්ථායිතා විශ්ලේෂණය
නියාමන පද්ධතියක ස්ථාවරත්වය පිළිබඳ සංකල්පය මෙම තත්වයෙන් පිටතට ගෙන ආ බාහිර බලවේග අතුරුදහන් වීමෙන් පසු සමතුලිත තත්වයට නැවත පැමිණීමේ හැකියාව සමඟ සම්බන්ධ වේ. ස්ථාවරත්වය යනු ස්වයංක්රීය පද්ධති සඳහා ප්රධාන අවශ්යතා වලින් එකකි.
ස්ථායීතාවය පිළිබඳ සංකල්පය ATS චලනය සඳහා දීර්ඝ කළ හැකිය:
- බාධාවකින් තොරව චලනය
- කෝපයට පත් ව්යාපාරය.
ඕනෑම පාලන පද්ධතියක චලනය විස්තර කරන්නේ අවකල සමීකරණයක් භාවිතා කර ඇති අතර එය සාමාන්යයෙන් පද්ධතියේ මෙහෙයුම් ආකාර 2 ක් විස්තර කරයි:
ස්ථාවර රාජ්ය මාදිලිය
රියදුරු මාදිලිය
මෙම අවස්ථාවේදී, ඕනෑම පද්ධතියක පොදු විසඳුම මෙසේ ලිවිය හැකිය:
![]()
බලෙන්සංරචකය තීරණය වන්නේ පාලන පද්ධතියේ ආදානය මත ආදාන බලපෑම මගිනි. සංක්රාන්ති ක්රියාවලීන් අවසානයේ පද්ධතිය මෙම තත්වයට ළඟා වේ.
සංක්රාන්තිආකෘතියේ සමජාතීය අවකල සමීකරණයක් විසඳීමෙන් සංරචකය තීරණය වේ:
සංගුණක a 0 ,a 1 ,...a n පද්ධති පරාමිති ඇතුළත් වේ => අවකල සමීකරණයේ ඕනෑම සංගුණකය වෙනස් කිරීම පද්ධති පරාමිති ගණනාවක වෙනසක් ඇති කරයි.
සමජාතීය අවකල සමීකරණයක විසඳුම
අනුකලනය නියතයන් කොහිද, සහ පහත දැක්වෙන ආකාරයේ ලාක්ෂණික සමීකරණයේ මූලයන් වේ:
ලාක්ෂණික සමීකරණය ශුන්යයට සමාන මාරු ශ්රිතයේ හරය නියෝජනය කරයි.
ලාක්ෂණික සමීකරණයේ මූලයන් සැබෑ, සංකීර්ණ සංයෝජන සහ සංකීර්ණ විය හැකිය, එය පද්ධතියේ පරාමිතීන් විසින් තීරණය කරනු ලැබේ.
පද්ධතිවල ස්ථාවරත්වය තක්සේරු කිරීම සඳහා, කිහිපයක් තිරසාර නිර්ණායක
සියලුම තිරසාර නිර්ණායක කණ්ඩායම් 3 කට බෙදා ඇත:
මූල
-  වීජීය
වීජීය
Nyquist ස්ථායීතා නිර්ණායකය 1932 දී ඇමරිකානු භෞතික විද්යාඥ H. Nyquist විසින් සකස් කර සාධාරණීකරණය කරන ලදී. පහත සඳහන් හේතූන් මත Nyquist ස්ථායීතා නිර්ණායකය ඉංජිනේරු භාවිතයේ බහුලව භාවිතා වේ:
- සංවෘත තත්වයක පද්ධතියේ ස්ථායිතාව එහි විවෘත කොටස W p (jw) හි සංඛ්යාත හුවමාරු ශ්රිතය මගින් අධ්යයනය කරනු ලබන අතර, මෙම ශ්රිතය බොහෝ විට සරල සාධක වලින් සමන්විත වේ. සංගුණක යනු පද්ධතියේ සැබෑ පරාමිතීන් වන අතර, ස්ථායීතා තත්වයන්ගෙන් ඒවා තෝරා ගැනීමට ඔබට ඉඩ සලසයි;
- ස්ථාවරත්වය අධ්යයනය කිරීම සඳහා, ඔබ ලබාගත් ප්රතිඵලවල නිරවද්යතාව වැඩි කරන පද්ධතියේ වඩාත් සංකීර්ණ මූලද්රව්යවල (පාලක වස්තුව, විධායක ආයතන) පර්යේෂණාත්මකව ලබාගත් සංඛ්යාත ලක්ෂණ භාවිතා කළ හැකිය;
- පද්ධතියේ ස්ථායීතාවය ලඝුගණක සංඛ්යාත ලක්ෂණ භාවිතයෙන් අධ්යයනය කළ හැකි අතර, එය ඉදිකිරීම අපහසු නැත;
- පද්ධතියේ ස්ථායීතා මායිම් ඉතා සරලව තීරණය වේ;
- ප්රමාදයක් සමඟ ATS හි ස්ථායිතාව තක්සේරු කිරීම සඳහා භාවිතා කිරීමට පහසුය.
Nyquist ස්ථායිතා නිර්ණායකය මඟින් ACS එකක විවෘත ලූප කොටසේ AFC මත පදනම්ව එහි ස්ථායීතාවය ඇගයීමට හැකි වේ. මෙම අවස්ථාවෙහිදී, Nyquist නිර්ණායකයේ යෙදීමේ අවස්ථා තුනක් වෙන්කර හඳුනාගත හැකිය.
1. ACS හි විවෘත කොටස ස්ථායී වේ.සංවෘත ලූප පද්ධතියක ස්ථායීතාවය සඳහා, වෙනස් කිරීමේදී පද්ධතියේ විවෘත-ලූප් කොටසේ (Nyquist hodograph) AFC ප්රතිචාරය අවශ්ය සහ ප්රමාණවත් වේ.සංඛ්යාත w 0 සිට +¥ දක්වා ඛණ්ඩාංක සමඟ ලක්ෂ්යය ආවරණය නොකළේය [-1, j 0]. රූපයේ. 4.6 ප්රධාන විය හැකි අවස්ථා පෙන්වයි:
1. - සංවෘත පද්ධතිය සම්පූර්ණයෙන්ම ස්ථායී වේ;
2. - ATS කොන්දේසි සහිත ස්ථායී වේ, i.e. සම්ප්රේෂණ සංගුණකයේ යම් යම් පරාසයක වෙනස්කම් තුළ පමණක් ස්ථාවර වේ කේ;
3. - ATS යනු ස්ථාවරත්වයේ මායිමේ ය;
4. - ATS අස්ථායි.
සහල්. 4.6 ACS හි විවෘත කොටස ස්ථායී වන විට Nyquist hodographs
2. ACS හි විවෘත කොටස ස්ථායීතා මායිමේ ඇත.මෙම අවස්ථාවෙහිදී, ලාක්ෂණික සමීකරණයට ශුන්ය හෝ සම්පූර්ණයෙන්ම මනඃකල්පිත මූලයන් ඇති අතර ඉතිරි මූලයන් සෘණාත්මක සැබෑ කොටස් ඇත.
සංවෘත පද්ධතියක ස්ථාවරත්වය සඳහා, පද්ධතියේ විවෘත-ලූප් කොටස ස්ථායීතා මායිමේ තිබේ නම්, වෙනස් කිරීමේදී පද්ධතියේ විවෘත-ලූප් කොටසෙහි AFC ප්රතිචාරය අවශ්ය සහ ප්රමාණවත් වේ. w 0 සිට +¥ දක්වා, අසීමිත විශාල අරය සහිත චාපයකින් විසන්ධි ප්රදේශයට අතිරේකව, ලක්ෂ්ය ඛණ්ඩාංක [-1, j 0]. පද්ධතියේ විවෘත-ලූප් කොටසේ AFC ප්රතිචාරයේ ν ශුන්ය මූලයන් ඉදිරියේ w=0 අසීමිත විශාල අරය සහිත චාපයකින් ධනාත්මක සැබෑ අර්ධ අක්ෂයේ සිට අංශක කෝණයකින් දක්ෂිණාවර්තව, රූපයේ දැක්වෙන පරිදි චලනය වේ. 4.7

සහල්. 4.7 ශුන්ය මූලයන් හමුවේ Nyquist hodographs
තනිකරම මනඃකල්පිත මූලයන් යුගලයක් තිබේ නම් w i =, පසුව AFC ප්රතිචාරය සංඛ්යාතය w iඅසීමිත විශාල අරය සහිත චාපයක් දක්ෂිණාවර්තව 180° කෝණයකින් චලනය වන අතර එය රූපයේ දැක්වේ. 4.8

සහල්. 4.8 Nyquist hodograph සම්පූර්ණයෙන්ම මනඃකල්පිත මූල යුගලයක් ඉදිරියේ
3. පද්ධතියේ විවෘත-ලූප් කොටස අස්ථායී වේ, i.e. ලාක්ෂණික සමීකරණය ඇත එල්ධනාත්මක සැබෑ කොටසක් සහිත මූලයන්. මෙම අවස්ථාවෙහිදී, සංවෘත ලූප පද්ධතියේ ස්ථායීතාවය සඳහා සංඛ්යාතය වෙනස් වන විට එය අවශ්ය හා ප්රමාණවත් වේ w ACS හි විවෘත කොටසේ 0 සිට +¥ දක්වා AFC ලක්ෂය ආවරණය කරයි
[-1, j 0) එල්ධනාත්මක දිශාවට 2 වතාවක් (වාමාවර්තව).
Nyquist hodograph හි සංකීර්ණ හැඩයක් සහිතව, Ya.Z විසින් යෝජනා කරන ලද Nyquist නිර්ණායකයේ වෙනත් සූත්රගත කිරීමක් භාවිතා කිරීම වඩාත් පහසු වේ. Tsypkin සංක්රාන්ති නීති භාවිතා කරයි. පද්ධතියේ විවෘත-ලූප් කොටසේ අදියර ප්රතිචාර ප්රතිචාරය වැඩි වීමත් සමඟ සංක්රමණය වීම wසැබෑ අක්ෂයේ -1 සිට -¥ දක්වා ඉහළ සිට පහළට ඇති කොටස ධනාත්මක ලෙස සලකනු ලැබේ (රූපය 4.9), සහ පහළ සිට ඉහළට සෘණ. AFC ප්රතිචාරය මෙම කොටසින් ආරම්භ වන්නේ නම් w=0 හෝ අවසන් වේ w=¥ , එවිට AFC අර්ධ සංක්රාන්තියක් සිදු කරන බව සලකනු ලැබේ.

සහල්. 4.9 P( කොටස හරහා Nyquist hodograph හි සංක්රාන්ති w) -¥ සිට -1 දක්වා
සංවෘත පද්ධතිය ස්ථායී වේ, -1 සිට -¥ දක්වා සැබෑ අක්ෂයේ කොටසක් හරහා Nyquist hodograph හි ධන සහ සෘණ සංක්රාන්ති සංඛ්යාව අතර වෙනස l/2 ට සමාන වේ නම්, l යනු ධනයක් සහිත ලාක්ෂණික සමීකරණයේ මූල ගණනයි. සැබෑ කොටස.
කාර්ය තත්ත්වය.
Mikhailov සහ Nyquist ස්ථායීතා නිර්ණායක භාවිතා කරමින්, විවෘත තත්වයේ පෝරමය මාරු කිරීමේ කාර්යයක් ඇති තනි පුඩුවක් පාලන පද්ධතියක ස්ථායිතාව තීරණය කරන්න.
විකල්පයට අනුව K, a, b සහ c හි අගයන් සූත්රයට ඇතුළත් කරන්න.
W(s) = ![]() ,
(1)
,
(1)
Mikhailov සහ Nyquist hodographs සාදන්න. පද්ධතියේ කපා හැරීමේ සංඛ්යාතය තීරණය කරන්න.
පද්ධතියේ ලාභයේ තීරණාත්මක අගය තීරණය කරන්න.
විසඳුමක්.
මෙහෙයුම් කලනය (Laplace Transform) වැනි බලවත් ගණිතමය උපකරණයක් භාවිතයෙන් පාලන පද්ධතිවල විශ්ලේෂණය සහ සංස්ලේෂණය පිළිබඳ ගැටළු විසඳනු ලැබේ. මෙහෙයුම් කලනය (Laplace Transform) වැනි බලවත් ගණිතමය උපකරණයක් භාවිතයෙන් පාලන පද්ධතිවල විශ්ලේෂණය සහ සංස්ලේෂණය පිළිබඳ ගැටළු විසඳනු ලැබේ. ක්රියාකරු සමීකරණයේ සාමාන්ය විසඳුම ලාක්ෂණික බහුපදයේ (බහුපද) මූලයන්ගේ අගයන් මගින් නිර්ණය කරන නියමයන්ගේ එකතුවයි.
ඩී(ය) = d s n ඈ n ) .
Mikhailov ගේ hodograph ඉදිකිරීම.
A) (1) සමීකරණය මගින් විස්තර කරන ලද සංවෘත පද්ධතිය සඳහා ලාක්ෂණික බහුපද අපි ලියන්නෙමු.
ඩී(s) = 50 + (25s+1)(0.1s+1)(0.01s+1) = 50+(625+50s+1)(0.001+0.11s+1) =0.625+68.85 +630.501+50.11s +51.
බහුපදයක මුල් ඩී(ය) විය හැක: null; සැබෑ (සෘණ, ධනාත්මක); මනඃකල්පිත (සෑම විටම යුගල, සංයෝජන) සහ සංකීර්ණ සංයුක්ත.
B) s→ ωj ආකෘතියට පරිවර්තනය කරන්න
ඩී()=0.625+68.85+630.501+50.11+51=0.625ω-68.85jω- 630.501ω+50.11jω+51
ω - සංඥා සංඛ්යාතය, j = (1) 1/2 - මනඃකල්පිත ඒකකය. J 4 =(-1) 4/2 =1, J 3 =(-1) 3/2 =-(1) 1/2 = - j, J 2 =(-1) 2/2 =-1, J =(-1) 1/2 = j,
C) අපි සැබෑ සහ මනඃකල්පිත කොටස් තෝරා ගනිමු.
ඩී= U()+jV(), මෙහි U() යනු සැබෑ කොටස වන අතර V() යනු මනඃකල්පිත කොටසයි.
U(ω) =0.625ω-630.501ω+51
V(ω) =ω(50.11-68.85ω)
D) අපි Mikhailov ගේ hodograph ගොඩනඟමු.
අපි Mikhailov ගේ hodograph එක බිංදුවට ආසන්නව සහ දුරින් ගොඩනඟමු; මේ සඳහා අපි 0 සිට +∞ දක්වා වෙනස් වන විට D(jw) ගොඩනඟමු. අපි ඡේදනය වන ස්ථාන සොයා ගනිමු යූ(w) සහ වී(w) අක්ෂ සහිත. Microsoft Excel භාවිතයෙන් ගැටළුව විසඳා ගනිමු.
අපි w හි අගයන් 0 සිට 0.0001 සිට 0.1 දක්වා පරාසයක සකසා ඒවා වගුවේ ගණනය කරමු. එක්සෙල් අගයන් යූ(ω) සහ වී(ω), D(ω); ඡේදනය වීමේ ස්ථාන සොයා ගන්න යූ(w) සහ වී(w) අක්ෂ සහිත,
අපි w හි අගයන් 0.1 සිට 20 දක්වා පරාසයක සකසා ඒවා වගුවේ ගණනය කරමු. එක්සෙල් අගයන් යූ(w) සහ වී(w), D; ඡේදනය වීමේ ස්ථාන සොයා ගන්න යූ(w) සහ වී(w) අක්ෂ සහිත.
වගුව 2.1 - සැබෑ සහ මනඃකල්පිත කොටස් සහ බහුපදයේම අර්ථ දැක්වීම ඩී()Microsoft Excel භාවිතා කිරීම






සහල්. A, B, ..... යැපීම් යූ(ω) සහ වී(ω), D(ω) සිට ω
රූපයට අනුව. A, B, .....ඡේදනය වන ස්ථාන සොයන්න යූ(w) සහ වී(w) අක්ෂ සහිත:
ω = 0 දී යූ(ω)=…. සහ වී(ω)= ……

Fig.1. Mikhailov ගේ hodograph ω = 0:000.1:0.1.

Fig.2. Mikhailov ගේ hodograph ω = 0.1:20
D) hodograph මත පදනම්ව පද්ධතියේ ස්ථාවරත්වය පිළිබඳ නිගමන.
ඕනෑම ගතික පද්ධතියක ස්ථාවරත්වය (සංකල්පයක් ලෙස) බාහිර බලපෑම ඉවත් කිරීමෙන් පසු එහි හැසිරීම මගින් තීරණය වේ, i.e. ආරම්භක කොන්දේසි වල බලපෑම යටතේ එහි නිදහස් චලනය. පද්ධතියක් මෙම තත්වයෙන් පිටතට ගෙන ආ සංඥාව (කැළඹීම) පද්ධතිය මත ක්රියා කිරීම නැවැත්වීමෙන් පසු එහි මුල් සමතුලිත තත්ත්වයට නැවත පැමිණේ නම් එය ස්ථාවර වේ. අස්ථායී පද්ධතියක් එහි මුල් තත්වයට නොපැමිණෙන නමුත් කාලයත් සමඟ එය අඛණ්ඩව ඉවතට ගමන් කරයි. පද්ධතියේ ස්ථාවරත්වය තක්සේරු කිරීම සඳහා, ගතික සමීකරණයට විසඳුමේ නිදහස් සංරචකය අධ්යයනය කිරීම අවශ්ය වේ, එනම් සමීකරණයට විසඳුම :.
ඩී(ය) = d s n ඈ n )= 0.
Mikhailov නිර්ණායකය භාවිතා කරමින් පද්ධතියේ ස්ථාවරත්වය පරීක්ෂා කරන්න :
මිහයිලොව් නිර්ණායක: ස්ථායී ASR සඳහා, ධනාත්මක සැබෑ අර්ධ අක්ෂයේ w = 0 වලින් ආරම්භ වන Mikhailov hodograph (රූපය 1 සහ Fig. 2 බලන්න), w ලෙස ධනාත්මක දිශාවට (වාමාවර්තව) අනුක්රමිකව ගමන් කිරීම අවශ්ය සහ ප්රමාණවත් වේ. 0 සිට ∞ n චතුරස්රයන් දක්වා වැඩි වේ, n යනු ලාක්ෂණික බහුපදයේ උපාධියයි.
හොඩොග්රැෆ් පහත නිර්ණායක කොන්දේසි තෘප්තිමත් කරන බව විසඳුමෙන් පැහැදිලිය (රූපය 1 සහ පය. 2) එය ආරම්භ වන්නේ ධනාත්මක සැබෑ අර්ධ අක්ෂයේ w = 0 හිදී ය. හොඩෝග්රැෆ් පහත නිර්ණායක කොන්දේසි සපුරාලන්නේ නැත: එය ω හි ධනාත්මක දිශාවට (බහුපද n=4 උපාධිය) හතරැස් හතරම වටේ යන්නේ නැත.
මෙම විවෘත-ලූප් පද්ධතිය ස්ථායී නොවන බව අපි නිගමනය කරමු .
Nyquist hodograph ඉදිකිරීම.
A) අපි (1) s→ ωj සූත්රයේ ආදේශනයක් කරමු
W(s) = ![]() =
=![]() ,
,
B) වරහන් විවෘත කර හරයේ සැබෑ සහ මනඃකල්පිත කොටස් ඉස්මතු කරන්න
C) සංයුජයෙන් ගුණ කර සැබෑ සහ මනඃකල්පිත කොටස් තෝරන්න
 ,
,

මෙහි U() යනු සැබෑ කොටස වන අතර V() යනු මනඃකල්පිත කොටසයි.
D) අපි Nyquist hodograph එකක් ගොඩනඟමු: - W() මත යැපීම.
Fig.3. Nyquist hodograph.
E) Nyquist නිර්ණායකය භාවිතයෙන් පද්ධතියේ ස්ථායීතාවය පරීක්ෂා කරමු:
Nyquist නිර්ණායක: විවෘත තත්වයේ ස්ථායී පද්ධතියක් සංවෘත තත්වයේ ස්ථායී වීමට නම්, Nyquist hodograph, සංඛ්යාතය ශුන්යයේ සිට අනන්තය දක්වා වෙනස් වන විට, ලක්ෂ්ය ඛණ්ඩාංක (-1; j0) වලින් ආවරණය නොකිරීම අවශ්ය වේ. .
Hodograph නිර්ණායකයේ සියලුම කොන්දේසි සපුරාලන බව විසඳුමෙන් පැහැදිලි වේ (රූපය 3 බලන්න).
hodograph එහි දිශාව දක්ෂිණාවර්තව වෙනස් කරයි
hodograph ලක්ෂ්යය ආවරණය නොකරයි (-1; j0)
මෙම විවෘත-ලූප් පද්ධතිය ස්ථාවර බව අපි නිගමනය කරමු .
පද්ධතියේ ලාභයේ තීරණාත්මක අගය තීරණය කිරීම.
A) 2 වන ඡේදයේ, සැබෑ සහ මනඃකල්පිත කොටස් දැනටමත් වෙන් කර ඇත

B) පද්ධති ලාභයේ තීරණාත්මක අගය සොයා ගැනීම සඳහා, පරිකල්පනීය කොටස ශුන්යයට සහ සැබෑ කොටස -1 ට සමාන කිරීම අවශ්ය වේ.
C) අපි දෙවන (2) සමීකරණයෙන් සොයා ගනිමු
සංඛ්යාංකය 0 විය යුතුය.
අපි ඒක පිළිගන්නවා එහෙනම්
C) පළමු (1) සමීකරණයට ආදේශ කර සොයා ගන්න
පද්ධතියේ තීරනාත්මක අගය ලබා ගැනීම.
සාහිත්යය:
1.ස්වයංක්රීය පාලනය පිළිබඳ සම්භාව්ය සහ නවීන න්යායේ ක්රම. වෙළුම 1.
ස්වයංක්රීය පාලන පද්ධතිවල විශ්ලේෂණය සහ සංඛ්යාන ගතිකත්වය. එම්: එඩ්. MSTU Bauman විසින් නම් කරන ලදී. 2000
2. Voronov A.A. ස්වයංක්රීය පාලනය පිළිබඳ න්යාය. T. 1-3, M., Nauka, 1992
සංකීර්ණ විචල්යයක ශ්රිත න්යායෙන් වැදගත් ප්රමේයයක් ප්රකාශ කරයි: සරලව සම්බන්ධිත C සමෝච්ඡයක් තුළ ශ්රිතය අද්විතීය වීමට ඉඩ හරින්න, ඊට අමතරව, මෙම සමෝච්ඡය මත අද්විතීය හා විශ්ලේෂණාත්මක විය යුතුය. C හි ශුන්යයට සමාන නොවේ නම් සහ C සමෝච්ඡය තුළ තිබිය හැක්කේ සීමිත ඒකීය ලක්ෂ්ය සංඛ්යාවක් (ධ්රැව) නම්, එවිට

මෙහි ශුන්ය සංඛ්යාව වන අතර, C හි ඇතුළත ඇති ධ්රැව සංඛ්යාව වන අතර, ඒ සෑම එකක්ම එහි ගුණත්වය අනුව සැලකිල්ලට ගනී.
මෙම ප්රමේයය Cauchy ගේ අවශේෂ ප්රමේයයෙන් සෘජුවම අනුගමනය කරයි, එහි සඳහන් වේ
ශුන්ය හා ධ්රැව දෙකෙහිම ඒකවචන ආරක්ෂා වී ඇති බව අපි ප්රතිස්ථාපනය කර සටහන් කරමු එවිට මෙම ඒකීය ලක්ෂ්යවල ඇති ශේෂයන් ශුන්යවල ධන ලකුණක් සහ සෘණ ලකුණක් සහිත ඒකීය ලක්ෂ්යවල ගුණයට සමාන වේ. ඉහත සූත්රගත කර ඇති ප්රමේයය දැන් පැහැදිලිය.
සම්බන්ධතාවය (11.2-1) ආකෘතියෙන් ද ලිවිය හැකිය

C සමෝච්ඡය සාමාන්යයෙන් සැබෑ සහ මනඃකල්පිත කොටස් දෙකම ඇති බැවින්, එහි ලඝුගණකය ආකෘතියෙන් ලියා ඇත.
C මායිමේ කොතැනකවත් අතුරුදහන් නොවේ නම්, (II.2-3) හි අනුකලනය සෘජුවම ලබා දෙයි

එහිදී සංවෘත සමෝච්ඡයේ අත්තනෝමතික ආරම්භය සහ අවසානය C. ප්රතිඵලයක් ලෙස,
ප්රතිඵල (II.2-1) සහ (II.2-7) ඒකාබද්ධ කිරීමෙන්, සමෝච්ඡය C වටා දිවෙන විට කෝණයෙහි සම්පූර්ණ වෙනසෙහි (සම්භවය වටා සම්පූර්ණ විප්ලවයේ) ගුණිතය අතර වෙනසට සමාන බව අපට පෙනී යයි C සමෝච්ඡය ඇතුළත ශුන්ය සහ පොලු.
C දුවන විට සම්භවය වටා ඇති මුළු විප්ලව ගණන නම්, අපට ලිවිය හැකිය
![]()
එපමනක් නොව, C සමෝච්ඡය ධන කෝණයේ වැඩි වීමකට අනුරූප වන දිශාවට ගමන් කරන අතර, ධනාත්මක කෝණයේ වැඩි වීමකට අනුරූප වන දිශාවට ද එය සිදු වුවහොත් විප්ලවය ධනාත්මක ලෙස හැඳින්වේ.

සහල්. II.2-1. දකුණු අර්ධ තලයේ සීමිත කොටස වසා ඇති සංවෘත සමෝච්ඡයක්.
දැන් මෙම ප්රතිඵල ස්ථාවරත්වය තීරණය කිරීමේ ගැටලුවට සෘජුවම යෙදිය හැකිය. හුවමාරු ශ්රිතයේ හරයෙහි දකුණු අර්ධ තලයේ ශුන්ය තිබේ දැයි දැන ගැනීමට අපට අවශ්යය.
එහි ප්රතිඵලයක් ලෙස, දකුණු අර්ධ තලය සම්පූර්ණයෙන්ම වසා දැමීමට සමෝච්ඡ C තෝරා ගනු ලැබේ. මෙම පරිපථය රූපයේ දැක්වේ. දකුණු අර්ධ තලය වටකර ඇති මහා අර්ධ වෘත්තාකාරය සම්බන්ධතා මගින් ලබා දී ඇත
සීමාව තුළ අනන්තයට නැඹුරු වන අතරතුර.
ලෙස ලියා ඇතැයි සිතමු
![]()
එහි සම්පූර්ණ කාර්යයක් වන අතර එයට පොදු සාධක නොමැත. අපි තවදුරටත් සංකීර්ණ තලයේ රූප සටහනක් ගොඩනඟමු, සමෝච්ඡය C දිගේ අගයන් වෙනස් කරමු. මෙම රූප සටහන අපට සංවෘත සමෝච්ඡයක් ලබා දෙනු ඇත. පොදුවේ ගත් කල, එය බහුපද ආකෘතියේ සම්පූර්ණ කාර්යයක් වනු ඇත, පැහැදිලිවම ගුවන් යානයේ සීමිත කොටසෙහි ධ්රැව නොමැත. එය ලෝකෝත්තර නම්, දකුණු අර්ධ තලයේ සීමිත කොටසෙහි ධ්රැව ගණන P තීරණය කළ යුතුය. P දැනගැනීම සහ C හරහා දිවෙන විට රූප සටහනෙන් නිර්ණය කිරීම, දැන් අපට සමීකරණය (II.2-8) අනුව දකුණු අර්ධ තලයේ ඇති ශුන්ය ගණන තීරණය කළ හැක.
![]()

සහල්. II.2-2. සරල තනි පරිපථ පාලන පද්ධතිය.
පද්ධතිය ස්ථාවර වීමට නම් එය බිංදුවට සමාන විය යුතුය. එහි ප්රතිඵලයක් වශයෙන්, මෙම නිර්ණායකයේ යෙදීමට අදියර දෙකක් ඇතුළත් වේ: පළමුවැන්න දකුණු අර්ධ තලයේ ධ්රැව නිර්ණය කිරීම වන අතර, දෙවනුව C ධාවනය වන විට රූප සටහනක් තැනීම සාමාන්යයෙන් ඉතා සරලව සිදු කෙරේ. දෙවැන්න සැලකිය යුතු දුෂ්කරතා ඉදිරිපත් කළ හැකිය, විශේෂයෙන් එය තුන්වන හෝ ඉහළ අනුපිළිවෙලක් නම් සහ එහි ලෝකෝත්තර නියමයන් තිබේ නම්.
ප්රතිපෝෂණ පාලන පද්ධතියක් සඳහා, සාමාන්ය ආකාරයෙන් රූපයේ දැක්වේ. විවෘත ලූප මාරු කිරීමේ කාර්යයක් භාවිතා කිරීමෙන් රූප සටහන් වල සංකීර්ණත්වය සැලකිය යුතු ලෙස අඩු කළ හැකිය. සංවෘත ලූප පද්ධතියක හුවමාරු ශ්රිතය සම්බන්ධතාවය මගින් විවෘත ලූප පද්ධතියක මාරු කිරීමේ කාර්යයට සම්බන්ධ වේ
![]()
එහිදී ධ්රැව සහ ශුන්ය දෙකම තිබිය හැක. ස්ථායීතාවයේ ගැටලුවකදී, එය නිවැරදි අර්ධ තලයේ පොලු තිබේදැයි දැන ගැනීම යෝග්ය වේ. මෙය ශ්රිතයේ ශුන්යයේ දකුණු අර්ධ තලයේ සිටීම හෝ ශ්රිතයේ වෙනස් වීම නිසා සිදුවන බලපෑම පැහැදිලි කිරීම සඳහා ශ්රිතයේ ශුන්යයන් -1 මගින් මාරු කිරීම හා සමාන වේ open-loop gain, සහ ඒ සමඟම Nyquist රූප සටහන ගොඩනැගීමේ කාර්යය අවම කිරීම, අපි විවෘත-ලූප් පද්ධතියේ ලාභය K වන ආකාරයෙන් හර ප්රකාශන (II.2-12) නැවත ලියන්නෙමු. දැන් ධ්රැව සම්බන්ධව බිංදුවලට සමාන වේ
Nyquist නිර්ණායකය යෙදීම සඳහා, අපි මුලින්ම ආවරණය වන සමෝච්ඡ C අඳින්නෙමු
සම්පූර්ණ දකුණු අර්ධ තලය. මෙයින් පසු, ලක්ෂ්යය වටා එකම චලනය සඳහා වන මුළු විප්ලව ගණන අපි ගණනය කරමු K ලාභය වෙනස් කිරීම ලක්ෂ්යයේ පිහිටීම පමණක් වෙනස් කරන අතර ස්ථානයට බලපාන්නේ නැත [-PPP හි ශ්රිතයේ P ධ්රැව ගණන තීරණය වේ. ශ්රිතයෙන් සෘජුවම, එය සරල සාධකවල නිෂ්පාදනයක ස්වරූපය තිබේ නම්, හෝ එයට බහුපද හෝ ලෝකෝත්තර ස්වරූපයක් තිබේ නම් ගණනය කිරීම වඩාත් අපහසු වේ. එවිට පද්ධතියේ ස්ථායීතාවය තීරණය වන්නේ සමීකරණයේ සෘජු යෙදුම (II.2-8) මගින් පිහිටුවනු ලැබේ.
![]()
එහි ප්රතිඵලයක් ලෙස, පද්ධතිය ස්ථායී වන්නේ එය ශුන්යයට සමාන නම් පමණි, එහිදී දැන් හරයේ ශුන්ය ගණන (II.2-12)

සහල්. II.2-3. මනඃකල්පිත අක්ෂය මත ධ්රැව වල බයිපාස් සහිත පරිපථවල හැකි වෙනස් කිරීම් දෙකක්.
මෙම පෝරමයේ නිර්ණායකය යොදන විට, දකුණු අර්ධ තලය ආවරණය කරමින් සමෝච්ඡය C තෝරා ගැනීම කෙරෙහි අවධානය යොමු කළ යුතුය. සම්බන්ධතාවය (11.2-1), සහ එම නිසා (11.2-13) සමෝච්ඡයේ C. දර්ශණය වන ශ්රිතයේ ඒකවචන නොමැති වීම අවශ්ය වේ. එහි මූලාරම්භයේ ධ්රැවයක් හෝ සංකීර්ණ සංයුජ ධ්රැව යුගල කිහිපයක් පවා ඇති විට නිතර සිදුවන අවස්ථා තිබේ. මනඃකල්පිත අක්ෂය. මෙම විශේෂ අවස්ථා විසඳීම සඳහා, Fig. II.2-3. ලක්ෂණ ධ්රැව නම්, නවීකරණය කරන ලද සමෝච්ඡය C රූපයේ දැක්වෙන පරිදි ඒවායේ දකුණට හෝ වමට ගමන් කළ හැකිය. පිළිවෙලින් II.2-3,a සහ II.2-3,b. ඒකීයත්වය ධ්රැවයක් නොවේ නම්, සමෝච්ඡය සෑම විටම එහි දකුණට ගමන් කළ යුතුය, මන්ද සම්බන්ධතාවය (II.2-1) C සමෝච්ඡය තුළ ධ්රැව වැනි ඒකීයත්වයන්ට පමණක් ඉඩ සලසයි. වම් පැත්තේ සිට මඟ හරින ලද මනඃකල්පිත අක්ෂය මත ඇති එම පොලු C සමෝච්ඡය තුළ පිහිටා ඇති අතර, එබැවින්, P හි සැලකිල්ලට ගත යුතුය. මෙම අවස්ථාවෙහිදී, ඒකීය ලක්ෂ්යයට ආසන්නව ඇති සමෝච්ඡය C සාමාන්යයෙන් ස්වරූපයෙන් තෝරා ගනු ලැබේ.
![]()
සීමාවේ සිට කෝණය වෙනස් වන විට ශුන්යයට නැඹුරු වේ.
සමෝච්ඡය C හරහා ගමන් කරන hodograph ප්රධාන වශයෙන් කොටස් හතරකින් සමන්විත වේ. Hodograph දී
මනඃකල්පිත අක්ෂයේ ඒකීයත්වයන් ආසන්නයේ හැර, හුදෙක් විවෘත ලූප පද්ධතියේ සංඛ්යාත ප්රතිචාරයයි. එබැවින්, සැබෑ අක්ෂයට සාපේක්ෂව එය කුමන්ත්රණය කිරීමෙන් hodograph at ලබා ගත හැක. අසීමිත අර්ධ වෘත්තාකාරයක් හරහා ගමන් කරන විට, භෞතිකව ශක්ය සියලු පද්ධති සඳහා වන අගය ශුන්ය හෝ, උපරිම වශයෙන්, සීමිත නියත අගයකි. අවසාන වශයෙන්, මනඃකල්පිත අක්ෂයේ ධ්රැව ආශ්රිතව කුඩා අර්ධ වෘත්තාකාර හරහා දිවෙන විට hodograph මෙම ශ්රිතයට සෘජුවම ප්රකාශනය (II.2-14) ආදේශ කිරීම මගින් තීරණය වේ. මේ අනුව, ක්රියාකාරී තලය මත සමෝච්ඡ C සිතියම්ගත කිරීම සම්පූර්ණ වේ.
මෙම පෝරමයේ නිර්ණායකය යොදන විට, එය මත පනවා ඇති සීමාවන්ගේ ස්වභාවය පැහැදිලි වේ. පළමුව, එයට දකුණු අර්ධ තලයේ තිබිය හැක්කේ ධ්රැව ආකාරයේ ඒකීයත්වයන් සීමිත සංඛ්යාවක් පමණි. දෙවනුව, එයට මනඃකල්පිත අක්ෂයේ තිබිය හැක්කේ සීමිත ඒකීය සංඛ්යාවක් (ධ්රැව හෝ ශාඛා ලක්ෂ්ය) පමණි. ශාඛා ලක්ෂ්ය වම් අර්ධ තලයේ පවතින තාක් සහ ශ්රිතයේ ප්රධාන අගය භාවිතා කරන්නේ නම්, ශාඛා ලක්ෂ්ය ඇති ශ්රිත ඇතුළත් කිරීමට ශ්රිත පන්තිය දිගු කළ හැක. තෙවනුව, මෙම ශ්රිතයේ නිරපේක්ෂ අගය, දකුණු අර්ධ තලය තුළ වෙනස් වන විට, 0 සහ 0 අතර පවතින බැවින්, සංඛ්යාංකයේ ඇති පෝරමයේ සැලකිය යුතු ලක්ෂණ වලට අවසර ඇත.
Nyquist නිර්ණායකයේ යෙදුම උදාහරණයක් සමඟ නිරූපණය කිරීම සුදුසුය. ප්රතිපෝෂණ සහිත පාලිත පද්ධතිය සම්බන්ධතා මගින් නිර්වචනය කිරීමට ඉඩ දෙන්න

ලබා දී ඇති මූලද්රව්යවල මාරු කිරීමේ කාර්යය අර්ධ තරංග චුම්බක ඇම්ප්ලිෆයර් සිට සංඛ්යාතයක ක්රියාත්මක වන ද්වි-අදියර ප්රේරක මෝටරයකට අනුරූප වේ. සෘණ තෙතමනය ඇතිවීම අඩු රෝටර් ප්රතිරෝධය සමඟ සම්බන්ධ වේ. පළමු ප්රශ්නය පැන නගී: ලබා දී ඇති මූලද්රව්ය ස්ථායීකරණය කළ හැක්කේ ලාභ සාධකය නිසා පමණක්ද? එබැවින් අපි තබමු
විවෘත-ලූප් පද්ධතියේ හුවමාරු කාර්යය ස්වරූපය ගනී
![]()
පළමුව, එහි දකුණු අර්ධ තලයේ ඇත්තේ එක් ධ්රැවයක් පමණක් බවත්, රූපයේ දැක්වෙන C සමෝච්ඡය හරහා ධාවනය වන විට මෙම ධ්රැවය ආසන්න වශයෙන් රූප සටහනක් ඇති බවත් අපි දකිමු. II.2-4, a, රූපයේ දැක්වේ. II.2-4, b සහ තෝරාගත් ලාභයේ ලක්ෂ්යය වටා එක් ධනාත්මක විප්ලවයක් ඇති බව පෙන්නුම් කරයි.

සහල්. II.2-4. Nyquist රූප සටහන් සඳහා උදාහරණ.
එබැවින්, සමීකරණය (II.2-13) මගින් ප්රකාශිත Nyquist නිර්ණායකය භාවිතා කරමින්, අපි ප්රතිඵලය වෙත පැමිණෙමු
K වැඩි කිරීම ගුණකය නිසා රූප සටහනේ කොටසෙහි සර්පිලාකාර ස්වභාවය හේතුවෙන් ධනාත්මක විප්ලවයන් විශාල සංඛ්යාවක් ඇතිවීමේ හැකියාව නිර්මාණය කරයි, එබැවින් K හි සියලුම ධනාත්මක අගයන් සඳහා පද්ධතිය අස්ථායී බව අපට නිගමනය කළ හැකිය.
K හි සෘණ අගයන් සඳහා, අපට මූලාරම්භයට සාපේක්ෂව අපගේ රූප සටහන භ්රමණය කර ලක්ෂ්යය වටා විප්ලව සලකා බැලිය හැකිය, නැතහොත් පවතින රූප සටහනක් භාවිතා කර දෙවන ක්රමය සරල ය; එය සෘජුවම පෙන්නුම් කරන්නේ, අවම වශයෙන්, අවට ධනාත්මක වර්ධනයන් නොමැති බවයි. මෙය K හි සෘණ අගයන් සඳහා දකුණු අර්ධ තලයේ අවම වශයෙන් එක් ශුන්යයක් ලබා දෙයි. එබැවින් K හි සියලුම ධන සහ සෘණ අගයන් සඳහා පද්ධතිය අස්ථායී බව අපි නිගමනය කරමු, එබැවින් යම් නිවැරදි කිරීමක් අවශ්ය වේ පද්ධතිය ස්ථාවර.
විවෘත-ලූප් පද්ධතියක සංඛ්යාත ප්රතිචාරය පර්යේෂණාත්මක දත්ත වලින් ගොඩනගා ඇති විට Nyquist නිර්ණායකය ද භාවිතා කළ හැක. විවෘත-ලූප් පද්ධතියේ මාරු කිරීමේ කාර්යය මෙම නඩුවේ ස්ථායී විය යුතු අතර, එබැවින්, දකුණු අර්ධ තලයේ පොලු තිබිය නොහැක, i.e. Nyquist hodograph නිවැරදිව ගොඩනැගීමට, ඉතා අඩු සංඛ්යාතවල පද්ධතියේ හැසිරීම නිවැරදිව තීරණය කිරීමට සැලකිලිමත් විය යුතුය.
බහු-ලූප් පද්ධති සඳහා Nyquist නිර්ණායකය යොදන විට, ඉදිකිරීම් අභ්යන්තර ලූපයෙන් ආරම්භ වන අතර පිටත ලූප දක්වා ඉදිරියට යයි, එක් එක් පුඩුවෙන් PPP හි ඇති ධ්රැව ගණන ප්රවේශමෙන් ගණනය කරයි. ප්රවාහ සටහන පරිවර්තනය කිරීමෙන් සමහර පරිපථ ඉවත් කිරීමෙන් මෙම ක්රමයට යොදන කාර්යය බොහෝ විට අඩු කළ හැකිය. බහු-ලූප් පද්ධති සඳහා hodograph ඉදිකිරීම සඳහා අනුපිළිවෙල තෝරා ගැනීම ව්යුහාත්මක රූප සටහන මත මෙන්ම, සමෝච්ඡයන් තුළ නිශ්චිත සහ නිවැරදි කිරීමේ මූලද්රව්යවල පිහිටීම මත රඳා පවතී.
බහුපදයක් ලෙස දක්වා ඇති විවෘත-ලූප් පද්ධතියක මාරු කිරීමේ කාර්යය භාවිතා කරමින් Nyquist hodographs තැනීම
ස්වයංක්රීය පද්ධතිවල ස්ථායීතාවය අධ්යයනය කිරීමේදී Nyquist සංඛ්යාත නිර්ණායකය විවෘත-ලූප් පද්ධතියක විස්තාරය-අදියර සංඛ්යාත ප්රතිචාරය මත පදනම් වන අතර පහත පරිදි සකස් කළ හැක:
n වන අනුපිළිවෙලෙහි විවෘත ලූප පද්ධතියක ලාක්ෂණික සමීකරණයේ ධන තාත්වික කොටසක් සහිත k මූලයන් (k = 0, 1, ..... n) සහ සෘණ තාත්වික කොටසක් සහිත n-k මූලයන් තිබේ නම්, ස්ථායීතාවය සඳහා සංවෘත-ලූප පද්ධතියක් විවෘත-ලූප් පද්ධතියක (Nyquist hodograph) විස්තාරය-අදියර සංඛ්යාත ප්රතිචාරයේ hodograph සංකීර්ණ තලයේ ලක්ෂ්යය (-1, j0) k p කෝණයකින් ආවරණය කිරීම අවශ්ය සහ ප්රමාණවත් වේ. එයම වන අතර, ධනාත්මක දිශාවෙහි ලක්ෂ්යය (-1, j0) ආවරණය කරයි, i.e. වාමාවර්තව, k වාර.
විවෘත-ලූප් පද්ධතියක ලාක්ෂණික සමීකරණයට ධනාත්මක තාත්වික කොටසක් (k = 0) සහිත මූලයන් නොමැති විට විශේෂ අවස්ථාව සඳහා, i.e. , එය විවෘත තත්වයේ ස්ථායී වන විට, Nyquist නිර්ණායකය පහත පරිදි සකස් කර ඇත:
සංඛ්යාතය 0 සිට වෙනස් වන විට විවෘත-ලූප් පද්ධතියේ විස්තාරය-අදියර සංඛ්යාත ප්රතිචාරය නම් ස්වයංක්රීය පාලන පද්ධතිය සංවෘත තත්වයේ ස්ථායී වේ? ඛණ්ඩාංක (-1, j0) සමඟ සංකීර්ණ තලයේ ලක්ෂ්යයක් ආවරණය නොකරයි.
Nyquist ස්ථායීතා නිර්ණායකය ප්රතිපෝෂණ සහිත පද්ධති සඳහා, විශේෂයෙන්ම ඉහළ පෙළේ පද්ධති සඳහා යෙදවීමට පහසු වේ.
Nyquist hodograph තැනීම සඳහා, අපි ප්රායෝගික පාඩම අංක 5 වෙතින් විවෘත-ලූප් පද්ධතියේ හුවමාරු කාර්යය සංකේතාත්මක ආකාරයෙන් භාවිතා කරමු.
චුම්බක ඇම්ප්ලිෆයර් සම්ප්රේෂණ සංගුණකය හැර, පද්ධතියේ සියලුම මූලද්රව්යවල දී ඇති පරාමිතීන් සඳහා අපි එය සංකේතාත්මක-ඩිජිටල් ආකාරයෙන් ලියන්නෙමු:
විස්තාරය-අදියර සංඛ්යාත ප්රතිචාරයේ සමීකරණය ලියා තථ්ය සහ මනඃකල්පිත සංඛ්යාත ලක්ෂණ තෝරා චුම්බක ඇම්ප්ලිෆයර්හි සංඛ්යාත සහ සම්ප්රේෂණ සංගුණකයේ ශ්රිතයක් ලෙස නයික්විස්ට් හොඩෝග්රැෆ් පවුලක් ගොඩනඟමු.
MathСad හි amplitude-phase සංඛ්යාත ප්රතිචාරයේ ප්රස්ථාරයක් සැලසුම් කිරීම

Fig.3. විවෘත-ලූප් පද්ධතියක කාර්යයක් ලෙස මාරු කිරීමේ කාර්යය සඳහා ඉදිකරන ලද Nyquist hodograph වක්ර පවුලක් කේ mu .
රූප සටහන 3 සිට Nyquist hodographs වලින් එකක් ඛණ්ඩාංක සමඟ ලක්ෂ්යය හරහා ගමන් කරන බව පැහැදිලිය. (j0, -1) . එහි ප්රතිඵලයක් ලෙස, චුම්බක ඇම්ප්ලිෆයර්හි සම්ප්රේෂණ සංගුණකයේ දී ඇති වෙනස්වීම් පරාසයක එහි තීරණාත්මක අගය ද ඇත. එය තීරණය කිරීම සඳහා, අපි පහත සම්බන්ධතා භාවිතා කරමු:

එබැවින්, චුම්බක ඇම්ප්ලිෆයර්හි විවේචනාත්මක සම්ප්රේෂණ සංගුණකය වන්නේ:
කේ mukr =11.186981170416560078
මෙය ඇත්ත වශයෙන්ම සිදු වන බව සහතික කර ගනිමු. මෙය සිදු කිරීම සඳහා, අපි චුම්බක ඇම්ප්ලිෆයර් සම්ප්රේෂණ සංගුණකයේ අගයන් තුනක් සඳහා Nyquist hodograph වක්ර සාදන්නෙමු: කේ mu = 0.6k mukr ; කේ mu = කි mukr ; කේ mu =1.2k mukr

Fig.4.
k mu = 0.6 k mukr; k mu = k mukr; k mu =1.2 k mukr
චුම්බක ඇම්ප්ලිෆයර්හි තීරනාත්මක සම්ප්රේෂණ සංගුණකය නිවැරදිව සොයාගත් බව රූපය 4 හි වක්ර තහවුරු කරයි.
l.a.ch.h භාවිතය. සහ පද්ධති ස්ථාවරත්වය විශ්ලේෂණය කිරීම සඳහා අදියර සංඛ්යාත ලක්ෂණ
ලඝුගණක විස්තාරය සංඛ්යාත ප්රතිචාරය (l.a.ch..x) සහ අදියර සංඛ්යාත ප්රතිචාරය අනුව පද්ධති ස්ථායීතාවය සඳහා වන නිර්ණායකය පහත පරිදි සකස් කළ හැක:
ධනාත්මක සංක්රාන්ති සංඛ්යා අතර වෙනස නම් (අදියර සංඛ්යාත ප්රතිචාරය μ(φ) = -180 රේඛාව හරහා පහළ සිට ඉහළට සංක්රමණය වීම) විවෘත තත්වයේ අස්ථායී ස්වයංක්රීය පාලන පද්ධතියක් සංවෘත තත්වයේ ස්ථායී වේ. ° ) සහ සෘණ සංක්රාන්ති සංඛ්යා (අදියර සංඛ්යාත ප්රතිචාරය c(n) = -180 රේඛාව හරහා ඉහළ සිට පහළට සංක්රමණය වීම ° ) c(sch) = -180 රේඛාව හරහා අදියර සංඛ්යාත ප්රතිචාර c(sch). ° l.a.h..x (L(u)> 0) සංඛ්යාත පරාසයේ ශුන්යයට සමාන වේ.
අදියර සංඛ්යාත ප්රතිචාරයක් ගොඩනැගීම සඳහා, සාමාන්ය ගතික සබැඳි ආකාරයෙන් මාරු කිරීමේ ශ්රිතය නිරූපණය කිරීම සුදුසුය.
සහ ප්රකාශනය භාවිතයෙන් අදියර ලක්ෂණය ගොඩනඟන්න:
«+» - හුවමාරු ශ්රිතයේ සංඛ්යාංකයේ සාමාන්ය ගතික සබැඳි වලට අනුරූප වේ;
«-« - හුවමාරු ශ්රිතයේ හරයේ සාමාන්ය ගතික සබැඳි වලට අනුරූප වේ.
අසමමිතික L.A.C.H ඉදිකිරීමට. අපි සාමාන්ය ගතික සබැඳි ආකාරයෙන් ඉදිරිපත් කර ඇති විවෘත-ලූප් පද්ධතියක මාරු කිරීමේ කාර්යය භාවිතා කරමු:
මෙය සිදු කිරීම සඳහා, අපි පෝරමයේ මාරු කිරීමේ කාර්යය භාවිතා කරමු:
මෙම හුවමාරු ශ්රිතය සාමාන්ය ගතික සබැඳි ආකාරයෙන් සිතමු:
සාමාන්ය ගතික සබැඳි වල පරාමිතීන් පහත දැක්වෙන පරිදි අර්ථ දක්වා ඇත:
අදියර ලාක්ෂණික සමීකරණයට පෝරමය ඇත:
අදියර සංඛ්යාත ප්රතිචාරය අක්ෂය හරහා ගමන් කරන සංඛ්යාතය අපි තීරණය කරමු c(w) = -180 °
ඉදිකිරීමට එල්.ඒ.සී.එච්. අපි ප්රකාශනය භාවිතා කරමු:
චුම්බක ඇම්ප්ලිෆයර් සම්ප්රේෂණ සංගුණකයේ අගයන් දෙකක් සඳහා l.a.f.x හි ප්රස්ථාර රූප සටහන 5 පෙන්වයි කේ mu = 10 සහ කි mu = 80 .

Fig.5.
l.a.h.h හි විශ්ලේෂණය සහ අදියර සංඛ්යාත ලක්ෂණ පෙන්නුම් කරන්නේ චුම්බක ඇම්ප්ලිෆයර්හි සම්ප්රේෂණ සංගුණකය වැඩි වීමත් සමග බවයි 8 සිට 80 දක්වා පද්ධතිය ස්ථාවර සිට අස්ථායී වේ. චුම්බක ඇම්ප්ලිෆයර්හි විවේචනාත්මක සම්ප්රේෂණ සංගුණකය අපි තීරණය කරමු.
පද්ධති ස්ථායීතා ආන්තික සඳහා අමතර අවශ්යතා නොමැති නම්, ඒවා සමාන ලෙස ගැනීම රෙකමදාරු කරනු ලැබේ:
DL(s) = -12db Ds(s) = 35°h 45
මෙම තත්ත්වය තෘප්තිමත් වන චුම්බක ඇම්ප්ලිෆයර්හි කුමන සම්ප්රේෂණ සංගුණකය මත අපි තීරණය කරමු.
රූප සටහන 6 හි දැක්වෙන ප්රස්ථාර මගින් ද මෙය සනාථ වේ.