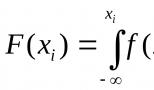අහඹු සිදුවීම් අනුකරණය. අඛණ්ඩ අහඹු විචල්‍යයක් වාදනය කිරීම. ප්‍රතිලෝම ශ්‍රිත ක්‍රමය අඛණ්ඩ අහඹු විචල්‍යයක හැකි අගයන් පහක් ක්‍රීඩා කරන්න

අර්ථ දැක්වීම 24.1.අහඹු සංඛ්යාහැකි අගයන් නම් කරන්න ආර්අඛණ්ඩ අහඹු විචල්‍යය ආර්, පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (0; 1).

1. විවික්ත අහඹු විචල්‍යයක් වාදනය කිරීම.

අපි හිතමු අපිට discrete random variable එකක් play කරන්න ඕන කියලා x, එනම්, බෙදාහැරීමේ නීතිය දැන ගැනීම, එහි හැකි අගයන් අනුපිළිවෙලක් ලබා ගැනීම x:

X x 1 x 2 … x n

ආර් ආර් 1 ආර් 2 … ආර් පී .

(0, 1) හි ඒකාකාරව බෙදා හරින ලද අහඹු විචල්‍යයක් සලකා බලන්න ආර්සහ ඛණ්ඩාංක සමඟ ලකුණු සමඟ පරතරය (0, 1) බෙදන්න ආර් 1, ආර් 1 + ආර් 2 , …, ආර් 1 + ආර් 2 +… +ආර් පී-1 මත පීඑකම දර්ශක සහිත සම්භාවිතාවන්ට දිග සමාන වන අර්ධ අන්තරයන්.

ප්රමේයය 24.1.විරාමයට වැටෙන සෑම අහඹු සංඛ්‍යාවකටම හැකි අගයක් පවරන්නේ නම්, වාදනය වන අගයට දී ඇති බෙදාහැරීමේ නීතියක් ඇත:

X x 1 x 2 … x n

ආර් ආර් 1 ආර් 2 … ආර් පී .

සාක්ෂි.

ප්රතිඵලය වන අහඹු විචල්යයේ විය හැකි අගයන් කට්ටලය සමඟ සමපාත වේ x 1 , x 2 ,… x n, විරාම ගණන සමාන බැවින් පී, සහ පහර දුන් විට ආර් ජේපරතරයකදී, සසම්භාවී විචල්‍යයකට ගත හැක්කේ එක් අගයක් පමණි x 1 , x 2 ,… x n.

නිසා ආර්ඒකාකාරව බෙදා හරිනු ලැබේ, එවිට එය එක් එක් පරතරය තුළට වැටීමේ සම්භාවිතාව එහි දිගට සමාන වේ, එයින් අදහස් වන්නේ එක් එක් අගය සම්භාවිතාවට අනුරූප වන බවයි p i. මේ අනුව, වාදනය වන අහඹු විචල්‍යයට දී ඇති බෙදාහැරීමේ නීතියක් ඇත.

උදාහරණයක්. විවික්ත අහඹු විචල්‍යයක අගයන් 10 ක් වාදනය කරන්න x, පෝරමය ඇති බෙදා හැරීමේ නීතිය: x 2 3 6 8

ආර් 0,1 0,3 0,5 0,1

විසඳුමක්. අපි අන්තරය (0, 1) අර්ධ කාල පරතරයන්ට බෙදමු: D 1 - (0; 0.1), D 2 - (0.1; 0.4), D 3 - (0.4; 0.9), D 4 - (0.9; 1). අහඹු සංඛ්‍යා වගුවෙන් අංක 10 ක් ලියමු: 0.09; 0.73; 0.25; 0.33; 0.76; 0.52; 0.01; 0.35; 0.86; 0.34. පළමු සහ හත්වන ඉලක්කම් D 1 පරතරය මත පිහිටා ඇත, එබැවින්, මෙම අවස්ථා වලදී, වාදනය කරන ලද අහඹු විචල්‍යය අගය ලබා ගනී x 1 = 2; තුන්වන, හතරවන, අටවන සහ දහවන ඉලක්කම් වලට අනුරූප වන D 2 පරතරයට වැටුණි x 2 = 3; දෙවන, පස්වන, හයවන සහ නවවන ඉලක්කම් D 3 පරතරය තුළ විය - මෙම අවස්ථාවේ දී X = x 3 = 6; පහුගිය ඉන්ටර්වල් එකේ නම්බර් තිබුණේ නෑ. එබැවින්, හැකි අගයන් ඉටු විය xවේ: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. ප්රතිවිරුද්ධ සිදුවීම් ක්රියා කිරීම.

එක් එක් සිද්ධිය සඳහා පරීක්ෂණ ක්‍රීඩා කිරීමට අවශ්‍ය වීමට ඉඩ දෙන්න ඒදන්නා සම්භාවිතාවක් සහිතව දිස්වේ ආර්. විවික්ත අහඹු විචල්‍යයක් සලකා බලන්න x, අගය 1 ගැනීම (සිදුවීම නම් ඒසිදු විය) සම්භාවිතාව සමඟ ආර්සහ 0 (නම් ඒසිදු නොවීය) සම්භාවිතාව සමඟ q = 1 – පි. ඊට පස්සේ අපි කලින් ඡේදයේ යෝජනා කළ පරිදි මෙම අහඹු විචල්‍යය වාදනය කරන්නෙමු.

උදාහරණයක්. අභියෝග 10 ක් ක්‍රීඩා කරන්න, එක් එක් සිදුවීමක් සමඟ ඒසම්භාවිතාව 0.3 සමඟ දිස්වේ.

විසඳුමක්. අහඹු විචල්‍යයක් සඳහා xබෙදා හැරීමේ නීතිය සමඟ x 1 0

ආර් 0,3 0,7

අපි D 1 - (0; 0.3) සහ D 2 - (0.3; 1) අන්තරයන් ලබා ගනිමු. අපි පෙර උදාහරණයේ ඇති අහඹු සංඛ්‍යා වල නියැදියම භාවිතා කරමු, ඒ සඳහා අංක 1, 3 සහ 7 සංඛ්‍යා D 1 අන්තරයට ද ඉතිරිය - D 2 පරතරයට ද වැටේ. ඒ නිසා ඒ සිද්ධිය කියලා අපිට හිතන්න පුළුවන් ඒපළමු, තුන්වන සහ හත්වන පරීක්ෂණ වලදී සිදු වූ නමුත් ඉතිරි පරීක්ෂණ වලදී සිදු නොවීය.

3. සම්පූර්ණ සිදුවීම් සමූහයක් සෙල්ලම් කිරීම.

සිදුවීම් නම් ඒ 1 , ඒ 2 , …, ඒ පී, සම්භාවිතාව සමාන වේ ආර් 1 , ආර් 2 ,… ආර් පී, සම්පූර්ණ කණ්ඩායමක් සාදන්න, පසුව ක්‍රීඩාව සඳහා (එනම්, පරීක්ෂණ මාලාවක ඔවුන්ගේ පෙනුමේ අනුපිළිවෙල ආදර්ශනය කිරීම), ඔබට විවික්ත අහඹු විචල්‍යයක් වාදනය කළ හැකිය. xබෙදා හැරීමේ නීතිය සමඟ x 1 2 … පී, 1 වන කරුණෙහි ඇති ආකාරයටම මෙය සිදු කර ඇත. ඒ සමඟම, අපි එය විශ්වාස කරමු

ආර් ආර් 1 ආර් 2 … ආර් පී

නම් xඅගය ගනී x i = i, පසුව මෙම පරීක්ෂණයේදී සිදුවීම සිදු විය A i.

4. අඛණ්ඩ අහඹු විචල්‍යයක් වාදනය කිරීම.

a) ප්‍රතිලෝම ශ්‍රිත ක්‍රමය.

අපි හිතමු අපිට අඛණ්ඩ සසම්භාවී විචල්‍යයක් වාදනය කිරීමට අවශ්‍යයි කියලා x, එනම්, එහි හැකි අගයන් අනුපිළිවෙලක් ලබා ගන්න x i (මම = 1, 2, …, n), බෙදා හැරීමේ කාර්යය දැන ගැනීම එෆ්(x).

ප්රමේයය 24.2.නම් ආර් අයියනු අහඹු අංකයකි, එවිට හැකි අගය x iඅඛණ්ඩ අහඹු විචල්‍යයක් වාදනය කරන ලදී xදී ඇති බෙදාහැරීමේ කාර්යයක් සමඟ එෆ්(x), අනුරූප ආර් අයි, සමීකරණයේ මුල වේ

එෆ්(x i) = ආර් අයි. (24.1)

සාක්ෂි.

නිසා එෆ්(x 0 සිට 1 දක්වා පරතරය තුළ ඒකාකාරී ලෙස වැඩි වේ, එවිට තර්කයේ (සහ අද්විතීය) අගයක් ඇත. x i, බෙදා හැරීමේ ශ්‍රිතය අගය ගනී ආර් අයි. මෙයින් අදහස් කරන්නේ සමීකරණයට (24.1) අද්විතීය විසඳුමක් ඇති බවයි: x i= එෆ් -1 (ආර් අයි), කොහෙද එෆ්-1 - ශ්‍රිතයට ප්‍රතිලෝමව එෆ්. සමීකරණයේ මුල (24.1) යනු සලකා බලන අහඹු විචල්‍යයේ විය හැකි අගයක් බව ඔප්පු කරමු. X.අපි මුලින්ම එය උපකල්පනය කරමු x iසමහර අහඹු විචල්‍ය x හි විය හැකි අගය වන අතර, x හි සම්භාවිතාව පරතරයට වැටෙන බව අපි ඔප්පු කරමු ( s, d) සමාන වේ එෆ්(ඈ) – එෆ්(c) ඇත්ත වශයෙන්ම, ඒකාකාරී බව නිසා එෆ්(x) සහ එය එෆ්(x i) = ආර් අයි. ඉන්පසු

එබැවින්, x හි සම්භාවිතාව පරතරයට වැටීම ( c, d) බෙදා හැරීමේ ශ්‍රිතයේ වර්ධකයට සමාන වේ එෆ්(x) මෙම පරතරය මත, එබැවින්, x = x.

අඛණ්ඩ අහඹු විචල්‍යයක හැකි අගයන් 3 ක් වාදනය කරන්න x, පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (5; 8).

එෆ්(x) =, එනම්, සමීකරණය විසඳීමට අවශ්ය වන්නේ අහඹු සංඛ්යා 3 ක් තෝරා ගනිමු: 0.23; 0.09 සහ 0.56 සහ ඒවා මෙම සමීකරණයට ආදේශ කරන්න. අනුරූප විය හැකි අගයන් ලබා ගනිමු x:

ආ) සුපිරි ස්ථාන ක්රමය.

වාදනය වන අහඹු විචල්‍යයේ ව්‍යාප්ති ශ්‍රිතය බෙදාහැරීමේ ශ්‍රිත දෙකක රේඛීය සංයෝජනයක් ලෙස නිරූපණය කළ හැකි නම්:

එවිට, කවදා සිට x®¥ එෆ්(x) ® 1.

අපි සහායක විවික්ත සසම්භාවී විචල්‍යයක් හඳුන්වා දෙමු Zබෙදා හැරීමේ නීතිය සමඟ

Z 12 අපි ස්වාධීන අහඹු සංඛ්යා 2ක් තෝරා ගනිමු ආර් 1 සහ ආර් 2 සහ හැකි දේ සෙල්ලම් කරන්න

පී සී 1 සී 2

අර්ථය Zඅංකය අනුව ආර් 1 (1 වන කරුණ බලන්න). නම් Z= 1, එවිට අපි අපේක්ෂිත හැකි අගය සොයමු xසමීකරණයෙන්, සහ නම් Z= 2, එවිට අපි සමීකරණය විසඳන්නෙමු.

මෙහිදී වාදනය වන සසම්භාවී විචල්‍යයේ ව්‍යාප්ති ශ්‍රිතය ලබා දී ඇති ව්‍යාප්ති ශ්‍රිතයට සමාන බව ඔප්පු කළ හැක.

c) සාමාන්‍ය අහඹු විචල්‍යයක ආසන්න වාදනය.

සඳහා සිට ආර්, (0, 1) හි ඒකාකාරව බෙදා හරිනු ලැබේ, පසුව එකතුව සඳහා පීස්වාධීන, ඒකාකාරව බෙදා හරින ලද අහඹු විචල්‍යයන් පරතරය (0,1). ඉන්පසුව, මධ්‍යම සීමාව ප්‍රමේයය මගින්, සාමාන්‍යකරණය වූ අහඹු විචල්‍යය at පී® ¥ පරාමිති සමඟ සාමාන්‍ය මට්ටමට ආසන්න බෙදා හැරීමක් ඇත ඒ= 0 සහ s =1. විශේෂයෙන්ම, විට තරමක් හොඳ ආසන්න අගයක් ලබා ගනී පී = 12:

එබැවින්, සාමාන්‍යකරණය වූ සාමාන්‍ය සසම්භාවී විචල්‍යයේ හැකි අගය ක්‍රීඩා කිරීමට x, ඔබට ස්වාධීන අහඹු සංඛ්‍යා 12ක් එකතු කර එකතුවෙන් 6ක් අඩු කළ යුතුය.

ප්රතිලෝම ශ්රිත ක්රමය

අපි හිතමු අපිට අඛණ්ඩ සසම්භාවී විචල්‍යයක් වාදනය කිරීමට අවශ්‍යයි කියලා x, එනම් එහි හැකි අගයන් අනුපිළිවෙලක් ලබා ගන්න x මම (මම= 1,2, ...), බෙදා හැරීමේ කාර්යය දැන ගැනීම එෆ්(x).

ප්රමේයය. නම් ආර් මම ,-අහඹු අංකය, පසුව හැකි අගයx මම දී ඇති බෙදාහැරීමේ ශ්‍රිතයක් සමඟ අඛණ්ඩ අහඹු විචල්‍ය X ක්‍රීඩා කරන ලදීඑෆ්(x), අනුරූපීආර් මම , සමීකරණයේ මුල වේ

එෆ්(x මම)= ආර් මම . (»)

සාක්ෂි. අහඹු අංකයක් තෝරා ගැනීමට ඉඩ දෙන්න ආර් මම (0≤ආර් මම <1). Так как в интервале всех возможных зна­чений xබෙදා හැරීමේ කාර්යය එෆ්(x) ඒකාකාරී ලෙස 0 සිට 1 දක්වා වැඩි වේ, එවිට මෙම පරතරය තුළ ඇත්තේ, සහ තර්කයේ එවැනි අගයක් පමණි. x මම , බෙදා හැරීමේ ශ්‍රිතය අගය ගනී ආර් මම. වෙනත් වචන වලින් කිවහොත්, (*) සමීකරණයට අද්විතීය විසඳුමක් ඇත

x මම = එෆ් - 1 (ආර් මම),

කොහෙද එෆ් - 1 - ප්රතිලෝම ශ්රිතය y=එෆ්(x).

අපි දැන් මූල බව ඔප්පු කරමු x මමසමීකරණය (*) යනු එවැනි අඛණ්ඩ අහඹු විචල්‍යයක විය හැකි අගයයි (අපි එය තාවකාලිකව දක්වන්නෙමු ξ , පසුව අපි එය සහතික කරමු ξ=Х) මේ සඳහා, අපි පහර සම්භාවිතාව බව ඔප්පු ξ විරාමයකට, උදාහරණයක් ලෙස ( සමග,ඈ), හැකි සෑම අගයකම පරතරයට අයත් වේ x, බෙදා හැරීමේ කාර්යයේ වර්ධකයට සමාන වේ එෆ්(x) මෙම පරතරය මත:

ආර්(සමග< ξ < ඈ)= එෆ්(ඈ)- එෆ්(සමග).

ඇත්ත වශයෙන්ම, සිට එෆ්(x)- හැකි සියලු අගයන් අතර පරතරය තුළ ඒකාකාරී ලෙස ශ්‍රිතය වැඩි කිරීම X,මෙම කාල පරතරය තුළ තර්කයේ විශාල අගයන් ශ්‍රිතයේ විශාල අගයන්ට අනුරූප වන අතර අනෙක් අතට. එබැවින්, නම් සමග <x මම < ඈ, එම එෆ්(c)< ආර් මම < එෆ්(ඈ), සහ අනෙක් අතට [එය සැලකිල්ලට ගනී (*) එෆ්(x මම)=ආර් මම ].

මෙම අසමානතා වලින් එය සසම්භාවී විචල්‍යයක් නම් ξ පරතරය තුළ අඩංගු වේ

සමග< ξ < ඈ, ξ (**)

එවිට සසම්භාවී විචල්‍යය ආර්පරතරය තුළ අඩංගු වේ

එෆ්(සමග)< ආර්< එෆ්(ඈ), (***)

සහ ආපසු. මේ අනුව, අසමානතා (**) සහ (***) සමාන වන අතර, එබැවින් සමානව සම්භාවිතාව:

ආර්(සමග< ξ< ඈ)=පී[එෆ්(සමග)< ආර්< එෆ්(ඈ)]. (****)

වටිනාකමේ සිට ආර්පරතරය (0,1) තුළ ඒකාකාරව බෙදා හරිනු ලැබේ, පසුව පහර දීමේ සම්භාවිතාව ආර්අන්තරයට (0,1) අයත් යම් පරතරයකට එහි දිගට සමාන වේ (XI පරිච්ඡේදය, § 6, සටහන බලන්න). විශේෂයෙන්ම,

ආර්[එෆ්(සමග)< ආර්< එෆ්(ඈ) ] = එෆ්(ඈ) - එෆ්(සමග).

එබැවින්, සම්බන්ධතාවය (****) ආකෘතියෙන් ලිවිය හැකිය

ආර්(සමග< ξ< ඈ)= එෆ්(ඈ) - එෆ්(සමග).

ඉතින්, පහර දීමේ සම්භාවිතාව ξ පරතරය තුළ ( සමග,ඈ) බෙදා හැරීමේ කාර්යයේ වර්ධකයට සමාන වේ එෆ්(x) මෙම පරතරය මත, එයින් අදහස් වන්නේ ξ=X.වෙනත් වචන වලින් කිවහොත්, සංඛ්යා x මම, (*) සූත්‍රය මගින් අර්ථ දක්වා ඇත්තේ ප්‍රමාණයේ විය හැකි අගයන් වේ X sබෙදාහැරීමේ කාර්යය ලබා දී ඇත එෆ්(x), Q.E.D.

රීතිය 1.x මම , අඛණ්ඩ අහඹු විචල්‍යය X,එහි බෙදා හැරීමේ කාර්යය දැන ගැනීම එෆ්(x), ඔබ අහඹු අංකයක් තෝරාගත යුතුය ආර් මමඑහි බෙදා හැරීමේ කාර්යයන් සමාන කර විසඳන්න x මම , ප්රතිඵලය සමීකරණය

එෆ්(x මම)= ආර් මම .

සටහන 1. මෙම සමීකරණය පැහැදිලිව විසඳීමට නොහැකි නම්, චිත්‍රක හෝ සංඛ්‍යාත්මක ක්‍රම වෙත යොමු වන්න.

උදාහරණය Iඅඛණ්ඩ අහඹු විචල්‍යයක හැකි අගයන් 3 ක් වාදනය කරන්න X,පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (2, 10).

විසඳුමක්. අපි ප්‍රමාණයේ බෙදා හැරීමේ කාර්යය ලියන්නෙමු X,පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ ( ඒ,බී) (XI පරිච්ඡේදය, § 3, උදාහරණය බලන්න):

එෆ්(x)= (හා)/ (බී-ඒ).

කොන්දේසිය අනුව, a = 2, බී=10, එබැවින්,

එෆ්(x)= (X- 2)/ 8.

මෙම ඡේදයේ රීතිය භාවිතා කරමින්, හැකි අගයන් සොයා ගැනීමට අපි සමීකරණයක් ලියන්නෙමු x මම , ඒ සඳහා අපි බෙදා හැරීමේ ශ්‍රිතය අහඹු අංකයකට සමාන කරමු:

(x මම -2 )/8= ආර් මම .

මෙතැන් සිට x මම =8 ආර් මම + 2.

අපි අහඹු අංක 3ක් තෝරා ගනිමු, උදාහරණයක් ලෙස, ආර් මම =0,11, ආර් මම =0,17, ආර් මම=0.66. සම්බන්ධව විසඳන ලද සමීකරණයට මෙම සංඛ්‍යා ආදේශ කරමු x මම , ප්රතිඵලයක් වශයෙන්, අපි අනුරූප විය හැකි අගයන් ලබා ගනිමු x: x 1 =8·0.11+2==2.88; x 2 =1.36; x 3 = 7,28.

උදාහරණ 2.අඛණ්ඩ අහඹු විචල්‍යය xබෙදා හැරීමේ ශ්‍රිතය මගින් නිශ්චිතව දක්වා ඇති ඝාතීය නියමය අනුව බෙදා හරිනු ලැබේ (පරාමිතිය λ > 0 දන්නා)

එෆ්(x)= 1 - ඊ - λ x (x>0).

හැකි අගයන් ඉටු කිරීමට අපට පැහැදිලි සූත්‍රයක් සොයාගත යුතුය X.

විසඳුමක්. මෙම ඡේදයේ රීතිය භාවිතා කරමින්, අපි සමීකරණය ලියන්නෙමු

1 - ඊ - λ x මම

සඳහා මෙම සමීකරණය විසඳා ගනිමු x මම :

ඊ - λ x මම = 1 - ආර් මම, හෝ - λ x මම = ln(1 - ආර් මම).

x මම =1p(1– ආර් මම)/λ .

අහඹු අංකය ආර් මමපරතරය (0,1) තුළ කොටා ඇත; එබැවින් අංක 1 වේ ආර් මම, ද අහඹු වන අතර පරතරය (0,1) ට අයත් වේ. වෙනත් වචන වලින් කිවහොත්, ප්රමාණ ආර්සහ 1 - ආර්සමානව බෙදා හරිනු ලැබේ. එබැවින්, සොයා ගැනීමට x මමඔබට සරල සූත්රයක් භාවිතා කළ හැකිය:

x මම =- ln ආර් මම /λ.

සටහන 2. එය දන්නා කරුණකි (XI පරිච්ඡේදය, §3 බලන්න)

විශේෂයෙන්ම,

සම්භාවිතා ඝනත්වය දන්නේ නම් එය පහත දැක්වේ f(x), පසුව සෙල්ලම් කිරීම සඳහා xඑය සමීකරණ වෙනුවට හැකි ය එෆ්(x මම)=ආර් මමසම්බන්ධයෙන් තීරණය කරන්න x මමසමීකරණය

රීතිය 2.හැකි අගය සොයා ගැනීමට x මම (අඛණ්ඩ සසම්භාවී විචල්‍යය X,එහි සම්භාවිතා ඝනත්වය දැන ගැනීම f(x) ඔබ අහඹු අංකයක් තෝරාගත යුතුය ආර් මමසහ ගැන තීරණය කරන්න x මම , සමීකරණය

හෝ සමීකරණය

කොහෙද ඒ-හැකි කුඩාම අවසාන අගය X.

උදාහරණය 3.අඛණ්ඩ අහඹු විචල්‍යයක සම්භාවිතා ඝනත්වය ලබා දී ඇත xf(x)=λ (1-λх/2) පරතරය තුළ (0; 2/λ); මෙම පරතරයෙන් පිටත f(x)= 0. හැකි අගයන් ඉටු කිරීමට අපට පැහැදිලි සූත්‍රයක් සොයාගත යුතුය X.

විසඳුමක්. රීතිය 2 ට අනුකූලව, අපි සමීකරණය ලියන්නෙමු

සඳහා අනුකලනය සිදු කිරීමෙන් සහ ප්රතිඵලය වන චතුරස්රාකාර සමීකරණය විසඳීමෙන් පසුව x මම, අපි අවසානයේ ලබා ගනිමු

අපි මුලින්ම මතක් කරමු අහඹු විචල්‍යයක් නම් ආර්පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (0,1), එවිට එහි ගණිතමය අපේක්ෂාව සහ විචලනය පිළිවෙලින් සමාන වේ (XII පරිච්ඡේදය, § 1, සටහන 3 බලන්න):

එම්(ආර්)= 1/2, (*)

ඩී(ආර්)= 1/2. (**)

අපි එකතුවක් හදමු පීස්වාධීන අහඹු විචල්‍යයන් පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (0,1) Rj(j=1, 2, ...,n):

මෙම එකතුව සාමාන්‍යකරණය කිරීම සඳහා, අපි මුලින්ම එහි ගණිතමය අපේක්ෂාව සහ විචලනය සොයා ගනිමු.

අහඹු විචල්‍යවල එකතුවේ ගණිතමය අපේක්ෂාව පදවල ගණිතමය අපේක්ෂාවන්ගේ එකතුවට සමාන බව දන්නා කරුණකි. ප්‍රමාණය (***) අඩංගු වේ පීනියමයන්, (*) නිසා එක් එක් ගණිතමය අපේක්ෂාව 1/2 ට සමාන වේ; එබැවින්, එකතුවේ ගණිතමය අපේක්ෂාව ( *** )

ස්වාධීන අහඹු විචල්‍යවල එකතුවේ විචලනය පදවල විචල්‍යයන්ගේ එකතුවට සමාන බව දන්නා කරුණකි. ප්‍රමාණය (***) අඩංගු වේ nස්වාධීන නියමයන්, (**) හේතුවෙන් එක් එක් විසරණය 1/12 ට සමාන වේ; එබැවින් එකතුවේ විචලනය (***)

එබැවින් එකතුවේ සම්මත අපගමනය (***)

අපි සලකා බලන මුදල සාමාන්‍යකරණය කරමු, ඒ සඳහා අපි ගණිතමය අපේක්ෂාව අඩු කර ප්‍රතිඵලය සම්මත අපගමනයෙන් බෙදන්නෙමු:

හි මධ්‍යම සීමාව ප්‍රමේයය මගින් p→∞මෙම සාමාන්‍යකරණය වූ අහඹු විචල්‍යයේ ව්‍යාප්තිය පරාමිති සමඟ සාමාන්‍ය තත්ත්වයට පත්වේ a= 0 සහ σ=1. අවසාන අවස්ථාවේදී පීබෙදා හැරීම ආසන්න වශයෙන් සාමාන්ය වේ. විශේෂයෙන්, කවදාද පී= 12 අපි ගණනය කිරීම් සඳහා තරමක් හොඳ සහ පහසු ආසන්න අගයක් ලබා ගනිමු

නීතිය.හැකි අගය සෙල්ලම් කිරීමට x iසාමාන්ය අහඹු විචල්යය x a=0 සහ σ=1 පරාමිති සමඟින්, ඔබට ස්වාධීන අහඹු සංඛ්‍යා 12ක් එකතු කර ලැබෙන එකතුවෙන් 6 අඩු කළ යුතුය:

උදාහරණයක්,අ) සාමාන්‍ය අගයේ හැකි අගයන් 100 ක් වාදනය කරන්න x a=0 සහ σ=1 පරාමිතීන් සමඟ; b) වාදනය කළ අගයෙහි පරාමිතීන් තක්සේරු කරන්න.

විසඳුමක්. අ) වගුවේ පළමු පේළියෙන් අහඹු අංක 12ක් තෝරා ගනිමු *), ඒවා එකතු කර ලැබෙන එකතුවෙන් 6 අඩු කරන්න; අවසානයේ අපට ඇත

x i=(0,10+0,09+...+0,67) - 6= - 0,99.

ඒ හා සමානව, වගුවේ සෑම ඊළඟ පේළියකින්ම පළමු අංක 12 තේරීමෙන්, ඉතිරි විය හැකි අගයන් අපි සොයා ගනිමු. X.

b) ගණනය කිරීම් සිදු කිරීමෙන් පසුව, අපි අවශ්ය ඇස්තමේන්තු ලබා ගනිමු:

සතුටුදායක ශ්‍රේණිගත කිරීම්: ඒ*ශුන්‍යයට ආසන්නව, σ* එකමුතුවෙන් සුළු වශයෙන් වෙනස් වේ.

අදහස් දක්වන්න. ඔබට හැකි අගයක් සෙල්ලම් කිරීමට අවශ්ය නම් z i, සාමාන්ය අහඹු විචල්යය Zගණිතමය අපේක්ෂාව සමඟ ඒසහ සම්මත අපගමනය σ , පසුව, මෙම ඡේදයේ රීතිය අනුව ක්රීඩා කළ හැකි අගය xi,සූත්‍රය භාවිතයෙන් අපේක්ෂිත අගය සොයා ගන්න

z i =σx i +a.

මෙම සූත්‍රය ලබා ගන්නේ සම්බන්ධයෙනි ( z i -a)/σ=x i.

කාර්යයන්

1. විවික්ත අහඹු විචල්‍යයක අගයන් 6 ක් වාදනය කරන්න X,එහි බෙදාහැරීමේ නීතිය වගුවක ආකාරයෙන් දක්වා ඇත

සටහන: නිශ්චිතභාවය සඳහා, අහඹු සංඛ්යා තෝරාගෙන ඇති බව උපකල්පනය කරන්න: 0.73; 0.75; 0.54; 0.08; 0.28; 0.53. නියෝජිත 10; 10; 10; 2; 3; 22; 10.

2. අත්හදා බැලීම් 4 ක් ක්‍රීඩා කරන්න, එක් එක් සිදුවීමක් සිදුවීමේ සම්භාවිතාව ඒ 0.52 ට සමාන වේ.

සටහන: නිසැක වීමට, අහඹු සංඛ්‍යා තෝරාගෙන ඇතැයි උපකල්පනය කරන්න: 0;28; 0.53; 0.91; 0.89.

නියෝජිත ඒ, , .

3. සම්පූර්ණ කණ්ඩායමක් පිහිටුවීමේ සිදුවීම් තුනක සම්භාවිතාව ලබා දී ඇත: ආර්(ඒ 1)=0,20, ආර්(ඒ 2)=0,32, ආර්(A 3)= 0,48. අභියෝග 6 ක් ක්‍රීඩා කරන්න, ඒ සෑම එකක් තුළම ලබා දී ඇති එක් සිදුවීමක් දිස් වේ.

සටහන: නිසැක වීමට, අහඹු සංඛ්යා තෝරාගෙන ඇති බව උපකල්පනය කරන්න: 0.77; 0.19; 0.21; 0.51; 0.99; 0.33

නියෝජිත A 3,ඒ 1 ,ඒ 2 ,ඒ 2 ,A 3,ඒ 2 .

4. සිදුවීම් ඒ සහ බීස්වාධීන සහ සහයෝගී. සිදුවීමක් සිදුවීමේ සම්භාවිතාව සහිත අභියෝග 5 ක් ක්‍රීඩා කරන්න ඒ 0.5 ට සමාන වේ, සහ සිදුවීම් තුල- 0,8.

ඒ 1 =AB, නිසැකවම, අහඹු සංඛ්යා ගන්න: 0.34; 0.41; 0.48; 0.21; 0.57.

නියෝජිත ඒ 1 ,ඒ 2 ,ඒ 2 ,ඒ 1 ,A 3.

5. සිදුවීම් ඒ, බී, සීස්වාධීන සහ සහයෝගී. සිදුවීම් සිදුවීමේ සම්භාවිතාව ලබා දී ඇති එක් එක් පරීක්ෂණ 4 ක් ක්‍රීඩා කරන්න: ආර්(ඒ)= 0,4, ආර්(තුල)= 0,6, ආර්(සමග)= 0,5.

සටහන: සම්පූර්ණ සිදුවීම් සමූහයක් සම්පාදනය කරන්න: නිසැකවම, අහඹු සංඛ්යා තෝරාගෙන ඇති බව උපකල්පනය කරන්න: 0.075; 0.907; 0.401; 0.344.

පිළිතුර A 1 ,ඒ 8,A 4,A 4.

6. සිදුවීම් ඒසහ තුලයැපෙන සහ සමුපකාර. පරීක්ෂණ 4 ක් ක්‍රීඩා කරන්න, ඒ සෑම එකක්ම සම්භාවිතාව ලබා දී ඇත: ආර්(ඒ)=0,7, ආර්(තුල)=0,6, ආර්(AB)=0,4.

සටහන: සම්පූර්ණ සිදුවීම් සමූහයක් සාදන්න: ඒ 1 =AB, නිසැකවම, අහඹු සංඛ්යා ගන්න: 0.28; 0.53; 0.91; 0.89.

නියෝජිත ඒ 1 , ඒ 2 , A 4 , A 3 .

7. අඛණ්ඩ අහඹු විචල්‍යයක හැකි අගයන් 3 ක් වාදනය කරන්න X,ඝාතීය නීතියට අනුව බෙදා හරින අතර බෙදා හැරීමේ ශ්‍රිතය මගින් නියම කර ඇත එෆ්(x)= 1 - ඉ -10 x .

සටහන: නිශ්චිතභාවය සඳහා, අහඹු සංඛ්යා තෝරාගෙන ඇති බව උපකල්පනය කරන්න: 0.67; 0.79; 0.91.

නියෝජිත 0,04; 0,02; 0,009.

8. අඛණ්ඩ අහඹු විචල්‍යයක හැකි අගයන් 4 ක් වාදනය කරන්න X,පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (6,14).

සටහන: නිශ්චිතභාවය සඳහා, අහඹු සංඛ්යා තෝරාගෙන ඇති බව උපකල්පනය කරන්න: 0.11: 0.04; 0.61; 0.93.

නියෝජිත 6,88; 6,32; 10,88; 13,44.

9. සුපිරි ස්ථාන ක්‍රමය භාවිතයෙන් අඛණ්ඩ අහඹු විචල්‍යයක් වාදනය කිරීම සඳහා පැහැදිලි සූත්‍ර සොයන්න X,බෙදාහැරීමේ කාර්යය ලබා දී ඇත

එෆ්(x)=1- (1/3)(2е- 2 x +е -3 x :), 0<x<∞.

නියෝජිත x= - (1/2)1п ආර් 2 නම් ආර් 1 < 2/3; x= - (1/3)1п ආර් 2 නම් ආර් 1 ≥2/3.

10. අඛණ්ඩ අහඹු විචල්‍යයක් වාදනය කිරීම සඳහා පැහැදිලි සූත්‍රයක් සොයන්න X,ලබා දී ඇති සම්භාවිතා ඝනත්වය f(x)=බී/(1 +පොරව 0≤ පරතරය තුළ 2 x≤1/(b-a); මෙම විරාමයෙන් පිටත f(x)=0.

නියෝජිත x i= - ආර් අයි/(b - ar i).

11. පරාමිති සමඟ සාමාන්‍ය අහඹු විචල්‍යයක හැකි අගයන් 2 ක් වාදනය කරන්න: a) ඒ=0, σ =1; බී) ඒ =2, σ =3.

සටහන: නිසැකවම, අහඹු සංඛ්‍යා පිළිගන්න (සියයෙන් ගණන පහත දක්වා ඇත; උදාහරණයක් ලෙස, අංක 74 අහඹු අංකයකට අනුරූප වේ ආර් 1 =0,74): 74. 10, 88, 82. 22, 88, 57, 07, 40, 15, 25, 70; 62, 88, 08, 78, 73, 95, 16, 05, 92, 21, 22, 30.

නියෝජිතඒ) x 1 = - 0,22, x 2 = - 0.10; 6) z 1 =1,34, z 2 =2,70.

විසිදෙවන පරිච්ඡේදය

අඛණ්ඩ සසම්භාවී විචල්‍ය X ක්‍රීඩා කිරීමට අවශ්‍ය වීමට ඉඩ හරින්න, i.e. F(x) බෙදා හැරීමේ ශ්‍රිතය දැන ගනිමින් එහි හැකි අගයන් (i=1, 2, ..., n) අනුපිළිවෙලක් ලබා ගන්න.

ප්රමේයය. සසම්භාවී සංඛ්‍යාවක් නම්, ලබා දී ඇති ව්‍යාප්ති ශ්‍රිතයක් සහිත F (x) සමඟ වාදනය කරන ලද අඛණ්ඩ සසම්භාවී විචල්‍ය X හි විය හැකි අගය , ට අනුරූප වන සමීකරණයේ මුල වේ.

රීතිය 1. හැකි අගය සොයා ගැනීමට, අඛණ්ඩ සසම්භාවී විචල්‍යයක් වන X, එහි ව්‍යාප්ති ශ්‍රිතය F (x) දැනගෙන, අහඹු අංකයක් තෝරා, එහි ව්‍යාප්ති ශ්‍රිතය සමාන කර එහි ප්‍රතිඵල සමීකරණය විසඳීම අවශ්‍ය වේ.

සටහන 1. මෙම සමීකරණය පැහැදිලිව විසඳීමට නොහැකි නම්, චිත්රක හෝ සංඛ්යාත්මක ක්රම වෙත යොමු වන්න.

උදාහරණ 1. අඛණ්ඩ අහඹු විචල්‍ය X හි හැකි අගයන් 3 ක් වාදනය කරන්න, පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (2, 10).

විසඳුම: අන්තරයේ (a, b) ඒකාකාරව බෙදා හරින ලද X අගයේ බෙදා හැරීමේ ශ්‍රිතය ලියමු: .

කොන්දේසිය අනුව, a=2, b=10, එබැවින්, .

රීතිය 1 භාවිතා කරමින්, අපි හැකි අගයන් සොයා ගැනීමට සමීකරණයක් ලියන්නෙමු, ඒ සඳහා අපි බෙදා හැරීමේ ශ්‍රිතය අහඹු අංකයකට සමාන කරමු:

මෙතැන් සිට .

අපි අහඹු අංක 3ක් තෝරා ගනිමු, උදාහරණයක් ලෙස, . සම්බන්ධව විසඳන ලද සමීකරණයට මෙම සංඛ්‍යා ආදේශ කරමු; එහි ප්‍රතිඵලයක් වශයෙන්, අපි X හි අනුරූප විය හැකි අගයන් ලබා ගනිමු: ; ; .

උදාහරණ 2. අඛණ්ඩ සසම්භාවී විචල්‍ය X බෙදාහැරීමේ ශ්‍රිතය (පරාමිතිය දන්නා) (x > 0) මගින් නිශ්චිතව දක්වා ඇති ඝාතීය නියමයකට අනුව බෙදා හැරේ. X හි විය හැකි අගයන් වාදනය කිරීම සඳහා අපට පැහැදිලි සූත්‍රයක් සොයාගත යුතුය.

විසඳුම: රීතිය භාවිතා කරමින්, අපි සමීකරණය ලියන්නෙමු.

අපි මෙම සමීකරණය විසඳමු: , හෝ .

අහඹු අංකය අන්තර් අන්තරයේ අඩංගු වේ (0, 1); එබැවින්, අංකය ද අහඹු වන අතර පරතරය (0,1) ට අයත් වේ. වෙනත් වචන වලින් කිවහොත්, R සහ 1-R අගයන් සමානව බෙදා හරිනු ලැබේ. එමනිසා, එය සොයා ගැනීමට, ඔබට සරල සූත්රයක් භාවිතා කළ හැකිය.

සටහන 2.එය දන්නා කරුණකි .

විශේෂයෙන්ම, .

එයින් කියවෙන්නේ සම්භාවිතා ඝනත්වය දන්නේ නම්, සමීකරණ වෙනුවට X වාදනය කිරීමට, සමීකරණය සඳහා විසඳිය හැකි බවයි.

රීතිය 2. අඛණ්ඩ සසම්භාවී විචල්‍ය X හි විය හැකි අගය සොයා ගැනීම සඳහා, එහි සම්භාවිතා ඝනත්වය දැන ගැනීම සඳහා, අහඹු අංකයක් තෝරාගෙන ඒ සඳහා සමීකරණය හෝ සමීකරණය විසඳිය යුතුය, එහිදී a යනු X හි කුඩාම අවසාන අගයයි.

උදාහරණ 3. අඛණ්ඩ අහඹු විචල්‍ය X හි සම්භාවිතා ඝනත්වය ලබා දී ඇත; මෙම පරතරයෙන් පිටත. X හි විය හැකි අගයන් වාදනය කිරීම සඳහා අපට පැහැදිලි සූත්‍රයක් සොයාගත යුතුය.

විසඳුම: රීතිය 2 ට අනුකූලව සමීකරණය ලියමු.

සඳහා අනුකලනය සිදු කිරීමෙන් සහ ප්රතිඵලය වන චතුරස්රාකාර සමීකරණය විසඳීමෙන් පසුව , අපි අවසානයේ එය ලබා ගන්නෙමු.

18.7 සාමාන්‍ය අහඹු විචල්‍යයක ආසන්න වාදනය

සසම්භාවී විචල්‍යයක් R පරතරය (0, 1) තුළ ඒකාකාරව බෙදා හරිනු ලැබුවහොත්, එහි ගණිතමය අපේක්ෂාව සහ විචල්‍යය පිළිවෙලින් සමාන වන බව අපි මුලින්ම සිහිපත් කරමු: M(R)=1/2, D(R)=1/12.

පරතරය තුළ (0, 1) ස්වාධීන, ඒකාකාරව බෙදා හරින ලද අහඹු විචල්‍ය n හි එකතුව සම්පාදනය කරමු: .

මෙම එකතුව සාමාන්‍යකරණය කිරීම සඳහා, අපි මුලින්ම එහි ගණිතමය අපේක්ෂාව සහ විචලනය සොයා ගනිමු.

අහඹු විචල්‍යවල එකතුවේ ගණිතමය අපේක්ෂාව පදවල ගණිතමය අපේක්ෂාවන්ගේ එකතුවට සමාන බව දන්නා කරුණකි. එකතුවෙහි n පද අඩංගු වේ, M(R) = 1/2 නිසා එක් එක් ගණිතමය අපේක්ෂාව 1/2 ට සමාන වේ; එබැවින්, එකතුවේ ගණිතමය අපේක්ෂාව

ස්වාධීන අහඹු විචල්‍යවල එකතුවේ විචලනය පදවල විචල්‍යයන්ගේ එකතුවට සමාන බව දන්නා කරුණකි. එකතුවෙහි n ස්වාධීන නියමයන් අඩංගු වේ, D(R) = 1/12 නිසා එක් එක් විචලනය 1/12 ට සමාන වේ; එබැවින්, එකතුවේ විචලනය

එබැවින් එකතුවේ සම්මත අපගමනය

අපි සලකා බලන මුදල සාමාන්‍යකරණය කරමු, ඒ සඳහා අපි ගණිතමය අපේක්ෂාව අඩු කර ප්‍රතිඵලය සම්මත අපගමනයෙන් බෙදන්නෙමු: .

මධ්‍යම සීමා ප්‍රමේයය අනුව, මෙම සාමාන්‍යකරණය වූ අහඹු විචල්‍යයේ ව්‍යාප්තිය a = 0 සහ පරාමිති සමඟ සාමාන්‍ය තත්ත්වයට නැඹුරු වේ. පරිමිත n සඳහා, බෙදා හැරීම ආසන්න වශයෙන් සාමාන්‍ය වේ. විශේෂයෙන්ම, n=12 සඳහා අපි ගණනය කිරීම් සඳහා තරමක් හොඳ සහ පහසු ආසන්න අගයක් ලබා ගනිමු.

ඇස්තමේන්තු සතුටුදායකයි: ශුන්‍යයට ආසන්න, එකකට වඩා ටිකක් වෙනස්.

භාවිතා කරන ලද මූලාශ්ර ලැයිස්තුව

1. ග්මර්මන් වී.ඊ. සම්භාවිතාව සහ ගණිතමය සංඛ්යාලේඛන පිළිබඳ න්යාය. - එම්.: උසස් පාසල, 2001.

2. Kalinina V.N., Pankin V.F. ගණිත සංඛ්යා ලේඛන. - එම්.: උසස් පාසල, 2001.

3. Gmurman V.E. සම්භාවිතා න්‍යාය සහ ගණිතමය සංඛ්‍යාලේඛන වල ගැටළු විසඳීම සඳහා මාර්ගෝපදේශයකි. - එම්.: උසස් පාසල, 2001.

4. Kochetkov E.S., Smerchinskaya S.O., Sokolov V.V. සම්භාවිතාව සහ ගණිතමය සංඛ්යාලේඛන පිළිබඳ න්යාය. – M.:FORUM:INFRA-M, 2003.

5. අගපොව් ජී.අයි. සම්භාවිතා න්‍යාය පිළිබඳ ගැටළු පොත. - එම්.: උසස් පාසල, 1994.

6. Kolemaev V.A., Kalinina V.N. සම්භාවිතාව සහ ගණිතමය සංඛ්යාලේඛන පිළිබඳ න්යාය. - එම්.: INFRA-M, 2001.

7. Ventzel E.S. සම්භාවිතා න්යාය. - එම්.: උසස් පාසල, 2001.

දැනුම පදනමේ ඔබේ හොඳ වැඩ යවන්න සරලයි. පහත පෝරමය භාවිතා කරන්න

සිසුන්, උපාධිධාරී සිසුන්, ඔවුන්ගේ අධ්‍යයන හා වැඩ කිරීමේදී දැනුම පදනම භාවිතා කරන තරුණ විද්‍යාඥයින් ඔබට ඉතා කෘතඥ වනු ඇත.

http://www.allbest.ru/ හි පළ කරන ලදී

පාඩම 1

දී ඇති බෙදාහැරීමේ නීතියක් සමඟ අහඹු සිදුවීම් අනුකරණය කිරීම

විවික්ත අහඹු විචල්‍යයක් වාදනය කිරීම

විවික්ත අහඹු විචල්‍යයක් වාදනය කිරීමට අවශ්‍ය වේ, i.e. X හි ව්‍යාප්ති නියමය දැන ගනිමින් එහි විය හැකි අගයන් x i (i = 1,2,3,...n) අනුපිළිවෙලක් ලබා ගන්න:

අපි අඛණ්ඩ සසම්භාවී විචල්‍යයක් R මගින් දක්වමු. R හි අගය පරතරය (0,1) තුළ ඒකාකාරව බෙදා හරිනු ලැබේ. r j (j = 1,2,...) සසම්භාවී විචල්‍යයේ R හි හැකි අගයන් දක්වයි. අපි අන්තරය 0 බෙදමු< R < 1 на оси 0r точками с координатами на n частичных интервалов.

එවිට අපට ලැබෙන්නේ:

i දර්ශකය සමඟ අර්ධ අන්තරයේ දිග එකම දර්ශකය සමඟ P සම්භාවිතාවට සමාන බව දැකිය හැකිය. දිග

මේ අනුව, අහඹු අංකයක් r i පරතරයට වැටෙන විට, සසම්භාවී විචල්‍ය X, සම්භාවිතාව P i සමඟ x i අගය ගනී.

පහත ප්‍රමේයය ඇත:

අන්තරයට වැටෙන සෑම අහඹු සංඛ්‍යාවක්ම විය හැකි අගයක් සමඟ සම්බන්ධ වේ නම් x i , එවිට වාදනය වන අගයට දී ඇති බෙදාහැරීමේ නීතියක් ඇත

බෙදාහැරීමේ නීතිය මගින් නිශ්චිතව දක්වා ඇති විවික්ත අහඹු විචල්‍යයක් වාදනය කිරීම සඳහා ඇල්ගොරිතම

1. 0r අක්ෂයේ අන්තරය (0,1) n අර්ධ අන්තරයන්ට බෙදීම අවශ්‍ය වේ:

2. (උදාහරණයක් ලෙස, අහඹු සංඛ්‍යා වගුවකින් හෝ පරිගණකයකින්) අහඹු අංකයක් තෝරන්න r j .

r j පරතරයට වැටුනේ නම්, වාදනය වන විවික්ත අහඹු විචල්‍යය විය හැකි අගයක් ගනී x i .

අඛණ්ඩ සසම්භාවී විචල්‍යයක් වාදනය කිරීම

අඛණ්ඩ සසම්භාවී විචල්‍ය X ක්‍රීඩා කිරීමට අවශ්‍ය වීමට ඉඩ හරින්න, i.e. එහි හැකි අගයන් x i (i = 1,2,...) අනුපිළිවෙලක් ලබා ගන්න. මෙම අවස්ථාවෙහිදී, බෙදාහැරීමේ ශ්රිතය F(X) දනී.

පවතී ඊළඟ ප්රමේයය.

r i යනු සසම්භාවී සංඛ්‍යාවක් නම්, r i ට අනුරූප දන්නා බෙදාහැරීමේ ශ්‍රිතයක් F(X) සමඟ වාදනය කරන ලද අඛණ්ඩ අහඹු විචල්‍ය X හි විය හැකි අගය x i සමීකරණයේ මුල වේ.

අඛණ්ඩ අහඹු විචල්‍යයක් වාදනය කිරීම සඳහා ඇල්ගොරිතම:

1. ඔබ අහඹු අංකයක් තෝරාගත යුතුය r i .

2. තෝරාගත් අහඹු අංකය දන්නා ව්‍යාප්ති ශ්‍රිතය F(X) ට සමාන කර සමීකරණයක් ලබා ගන්න.

3. x i සඳහා මෙම සමීකරණය විසඳන්න. ලැබෙන අගය x i එකවර අහඹු අංකයට අනුරූප වේ r i . සහ ලබා දී ඇති බෙදාහැරීමේ නීතිය F(X).

උදාහරණයක්. අඛණ්ඩ අහඹු විචල්‍ය X හි හැකි අගයන් 3 ක් වාදනය කරන්න, පරතරය තුළ ඒකාකාරව බෙදා හරිනු ලැබේ (2; 10).

X අගයෙහි ව්‍යාප්ති ශ්‍රිතයට පහත පෝරමය ඇත:

කොන්දේසිය අනුව, a = 2, b = 10, එබැවින්,

අඛණ්ඩ අහඹු විචල්‍යයක් වාදනය කිරීමේ ඇල්ගොරිතමයට අනුකූලව, අපි F(X) තෝරාගත් අහඹු අංකයට සමාන කරමු r i .. අපි මෙතැනින් ලබා ගනිමු:

මෙම සංඛ්‍යා සමීකරණයට ආදේශ කරන්න (5.3) අපි x හි අනුරූප අගයන් ලබා ගනිමු:

දී ඇති බෙදාහැරීමේ නීතියක් සමඟ අහඹු සිදුවීම් ආකෘතිකරණය කිරීමේ ගැටළු

1. විවික්ත අහඹු විචල්‍යයක අගයන් 10 ක් වාදනය කිරීම අවශ්‍ය වේ, i.e. X i (i=1,2,3,...n), බෙදාහැරීමේ නියමය X දැනගෙන එහි හැකි අගයන් අනුපිළිවෙලක් ලබා ගන්න

අහඹු සංඛ්‍යා වගුවෙන් අහඹු අංකයක් තෝරා ගනිමු r j: 0.10; 0.12; 0.37; 0.09; 0.65; 0.66; 0.99; 0.19; 0.88; 0.59; 0.78

2. සේවාව සඳහා ඉල්ලීම් ලැබීමේ වාර ගණන ඝාතීය බෙදා හැරීමේ නීතියට යටත් වේ (), x, පරාමිතිය l දන්නා (මෙතැන් සිට l = 1/t - ඉල්ලීම් ලැබීමේ තීව්‍රතාවය)

l=0.5 ඉල්ලීම්/පැයට. අයදුම්පත් ලැබීම් අතර කාල පරතරයන් සඳහා අගයන් අනුපිළිවෙල තීරණය කරන්න. ක්රියාත්මක කිරීම් සංඛ්යාව 5. අංකය r j: 0.10; 0.12; 0.37; 0.09; 0.65; 0.99;

පාඩම 2

පෝලිම් පද්ධතිය

එක් අතකින්, ඕනෑම ආකාරයක සේවාවක කාර්ය සාධනය සඳහා දැවැන්ත ඉල්ලීම් ඇති පද්ධති සහ අනෙක් අතට, මෙම ඉල්ලීම් තෘප්තිමත් වන පද්ධති, පෝලිම් පද්ධති ලෙස හැඳින්වේ. ඕනෑම QS ඉල්ලීම් ප්‍රවාහය ඉටු කිරීමට සේවය කරයි.

QS වලට ඇතුළත් වන්නේ: අවශ්‍යතා මූලාශ්‍රය, එන ප්‍රවාහය, පෝලිම්, සේවා උපාංගය, පිටතට යන ඉල්ලීම් ප්‍රවාහය.

SMO වලට බෙදා ඇත:

පාඩු සහිත QS (අසාර්ථක)

පොරොත්තු සහිත පෝලිම (අසීමිත පෝලිම් දිග)

සීමිත පෝලිම් දිග සහිත QS

සීමිත පොරොත්තු කාලය සහිත QS.

නාලිකා හෝ සේවා උපාංග ගණන මත පදනම්ව, QS පද්ධති තනි නාලිකාවක් හෝ බහු-නාලිකාවක් විය හැකිය.

අවශ්‍යතා ප්‍රභවයේ පිහිටීම අනුව: විවෘත සහ වසා ඇත.

අවශ්යතාව අනුව සේවා මූලද්රව්ය ගණන අනුව: තනි-අදියර සහ බහු-අදියර.

වර්ගීකරණයේ එක් ආකාරයක් වන්නේ D. Kendall වර්ගීකරණයයි - A/B/X/Y/Z

A - පැමිණීම අතර කාලය බෙදා හැරීම තීරණය කරයි;

B - සේවා කාලය බෙදා හැරීම තීරණය කරයි;

X - සේවා නාලිකා ගණන තීරණය කරයි;

Y - පද්ධතියේ ධාරිතාව තීරණය කරයි (පෝලිමේ දිග);

Z - සේවා අනුපිළිවෙල තීරණය කරයි.

පද්ධති ධාරිතාව අසීමිත වන විට සහ සේවා පෝලිම පළමුව පැමිණෙන විට පළමු සේවා මූලධර්මය අනුගමනය කරන විට, Y/Z කොටස් මඟ හැරේ. පළමු ඉලක්කම් (A) පහත සංකේත භාවිතා කරයි:

M-බෙදාහැරීමට ඝාතීය නීතියක් ඇත,

G-සේවා ක්‍රියාවලිය පිළිබඳ කිසිදු උපකල්පනයක් නොමැති වීම, නැතහොත් එය පුනරාවර්තන සේවා ක්‍රියාවලියක් යන අර්ථය ඇති GI සංකේතය සමඟ හඳුනාගෙන ඇත.

D- නියතිවාදී (ස්ථාවර සේවා කාලය),

E n - Erlang n වන අනුපිළිවෙල,

NM n - අධි-Erlang n වන අනුපිළිවෙල.

දෙවන ඉලක්කම් (B) එකම සංකේත භාවිතා කරයි.

සිව්වන ඉලක්කම් (Y) බෆර ධාරිතාව පෙන්වයි, i.e. පෝලිමේ උපරිම ස්ථාන ගණන.

පස්වන ඉලක්කම් (Z) පොරොත්තු පද්ධතියක පෝලිමේ සිට තෝරා ගැනීමේ ක්‍රමය දක්වයි: SP-සමාන සම්භාවිතාව, FF-පළමුවෙන්-පළමුවෙන් පිටතට, LF-අන්තිමයෙන්-පළමුවෙන් පිටතට, PR-ප්‍රමුඛතාවය.

කාර්යයන් සඳහා:

l යනු කාල ඒකකයකට ලැබෙන සාමාන්‍ය අයදුම්පත් සංඛ්‍යාවයි

µ - කාල ඒකකයකට සේවය කරන සාමාන්‍ය යෙදුම් සංඛ්‍යාව

නාලිකාව 1 පැටවීමේ සාධකය, හෝ නාලිකාව කාර්යබහුල කාල ප්‍රතිශතය.

ප්රධාන ලක්ෂණ:

1) P ප්‍රතික්ෂේප කිරීම - අසාර්ථක වීමේ සම්භාවිතාව - පද්ධතිය සේවාව ප්‍රතික්ෂේප කිරීමේ සම්භාවිතාව සහ අවශ්‍යතාවය නැති වී යයි. නාලිකාවක් හෝ සියලුම නාලිකා කාර්යබහුල වූ විට මෙය සිදු වේ (TFoP).

බහු-නාලිකාවක් සඳහා QS P විවෘත =P n, මෙහි n යනු සේවා නාලිකා ගණනයි.

සීමිත පෝලිම් දිගක් සහිත QS සඳහා P විවෘත =P n + l, මෙහි l යනු අවසර ලත් පෝලිම් දිග වේ.

2) සාපේක්ෂ q සහ නිරපේක්ෂ A පද්ධති ධාරිතාව

q= 1-P විවෘත A=ql

3) පද්ධතියේ මුළු අවශ්‍යතා ගණන

L sys = n - SMO සඳහා අසාර්ථකත්වයන් සමඟ, n යනු සේවා කිරීම මගින් අල්ලාගෙන සිටින නාලිකා ගණනයි.

QS සඳහා රැඳී සිටීම සහ සීමිත පෝලිම් දිග

L sys = n+L සිසිල්

මෙහි L cool යනු සේවාව ආරම්භ කිරීමට බලා සිටින සාමාන්‍ය ඉල්ලීම් ගණන යනාදිය.

අපි ගැටළු විසඳන විට ඉතිරි ලක්ෂණ සලකා බලමු.

තනි නාලිකා සහ බහු නාලිකා පෝලිම් පද්ධති. අසමත්වීම් සහිත පද්ධති.

සම්භාවිතා ආදාන ප්‍රවාහයක් සහ සේවා ක්‍රියා පටිපාටියක් සහිත සරලම තනි නාලිකා ආකෘතිය යනු අවශ්‍යතා ලැබීම් සහ සේවා කාල සීමාවන් අතර කාලසීමාවන් දෙකෙහිම ඝාතීය ව්‍යාප්තියකින් සංලක්ෂිත ආකෘතියකි. මෙම අවස්ථාවෙහිදී, ඉල්ලීම් ලැබීම් අතර කාල පරතරයන්හි බෙදාහැරීමේ ඝනත්වය පෝරමය ඇත

සේවා කාලය බෙදා හැරීමේ ඝනත්වය:

ඉල්ලීම් සහ සේවා ගලායාම සරලයි. පද්ධතියේ අසාර්ථකත්වය සමඟ වැඩ කිරීමට ඉඩ දෙන්න. දේශීය ජාල වල සම්ප්රේෂණ නාලිකා ආකෘති නිර්මාණය කිරීමේදී මෙම වර්ගයේ QS භාවිතා කළ හැකිය. පද්ධතියේ නිරපේක්ෂ හා සාපේක්ෂ ප්‍රතිදානය තීරණය කිරීම අවශ්‍ය වේ. මෙම පෝලිම් පද්ධතිය ප්‍රස්ථාරයක ස්වරූපයෙන් සිතමු (රූපය 2), එහි ප්‍රාන්ත දෙකක් ඇත:

S 0 - නාලිකාව නොමිලේ (බලා සිටීම);

S 1 - නාලිකාව කාර්යබහුලයි (ඉල්ලීම සේවා වෙමින් පවතී).

රූපය 2. අසාර්ථකත්වයන් සහිත තනි නාලිකා QS හි රාජ්ය ප්රස්ථාරය

අපි රාජ්ය සම්භාවිතාව සඳහන් කරමු: P 0 (t) - "නාලිකාව නිදහස්" තත්වයේ සම්භාවිතාව; P 1 (t) - "නාලිකාව කාර්යබහුල" තත්වයේ සම්භාවිතාව. ලේබල් කරන ලද රාජ්‍ය ප්‍රස්ථාරය භාවිතා කරමින්, අපි රාජ්‍ය සම්භාවිතා සඳහා කොල්මොගොරොව් අවකල සමීකරණ පද්ධතියක් සම්පාදනය කරමු:

රේඛීය අවකල සමීකරණ පද්ධතියට P 0 (t) + P 1 (t) = 1 යන සාමාන්‍ය තත්ත්වය සැලකිල්ලට ගනිමින් විසඳුමක් ඇත. මෙම පද්ධතියේ විසඳුම අස්ථායී ලෙස හැඳින්වේ, එය කෙලින්ම t මත රඳා පවතින අතර මේ ආකාරයට පෙනේ:

P 1 (t) = 1 - P 0 (t) (3.4.3)

අසාර්ථකත්වයන් සහිත තනි නාලිකා QS සඳහා, P 0 (t) සම්භාවිතාව q පද්ධතියේ සාපේක්ෂ ධාරිතාවට වඩා වැඩි දෙයක් නොවන බව තහවුරු කිරීම පහසුය. ඇත්ත වශයෙන්ම, P 0 යනු එම අවස්ථාවේ දී නාලිකාව නොමිලේ වන අතර t වේලාවට පැමිණෙන ඉල්ලීමක් සේවා සැපයීමේ සම්භාවිතාව වන අතර, එම නිසා, යම් කාලයක් සඳහා t ලබා දුන් ඉල්ලීම් සංඛ්‍යාවේ සාමාන්‍ය අනුපාතය ලැබුණු සංඛ්‍යාවට P 0 (t), i.e q = P 0 (t) ට ද සමාන වේ.

විශාල කාල පරතරයකින් පසු (at), ස්ථාවර (ස්ථාවර) මාදිලියක් සාක්ෂාත් කරගනු ලැබේ:

සාපේක්ෂ ප්‍රතිදානය දැන ගැනීමෙන් නිරපේක්ෂ එක සොයා ගැනීම පහසුය. නිරපේක්ෂ ප්‍රතිදානය (A) යනු පෝලිම් පද්ධතියකට කාල ඒකකයකට සේවය කළ හැකි සාමාන්‍ය ඉල්ලීම් ගණනයි:

ඉල්ලීමක් සැපයීම ප්‍රතික්ෂේප කිරීමේ සම්භාවිතාව "නාලිකාව කාර්යබහුල" තත්වයේ සම්භාවිතාවට සමාන වේ:

P open හි මෙම අගය ඉදිරිපත් කරන ලද අයැදුම්පත් අතර සේවය නොකළ අයදුම්පත් වල සාමාන්‍ය කොටස ලෙස අර්ථ දැක්විය හැක.

බොහෝ අවස්ථාවන්හිදී, ප්‍රායෝගිකව, පෝලිම් පද්ධති බහු-නාලිකාවක් වන අතර, එබැවින්, n සේවා සපයන නාලිකා (n>1 නම්) සහිත ආකෘති නිසැකවම උනන්දුවක් දක්වයි. මෙම ආකෘතිය මගින් විස්තර කරන ලද පෝලිම් ක්‍රියාවලිය ආදාන ප්‍රවාහයේ තීව්‍රතාවය මගින් සංලක්ෂිත වේ, n සේවාදායකයින්ට (යෙදුම්) වඩා සමාන්තරව සේවය කළ නොහැක. එක් ඉල්ලීමක් සඳහා සාමාන්‍ය සේවා කාලය 1/m වේ. ආදාන සහ ප්‍රතිදාන ප්‍රවාහයන් Poisson වේ. විශේෂිත සේවා නාලිකාවක මෙහෙයුම් ආකාරය පද්ධතියේ අනෙකුත් සේවා නාලිකා වල මෙහෙයුම් ආකාරය කෙරෙහි බලපාන්නේ නැත, සහ එක් එක් නාලිකාව සඳහා සේවා පටිපාටියේ කාලසීමාව ඝාතීය බෙදා හැරීමේ නීතියකට යටත්ව අහඹු විචල්‍යයකි. n සමාන්තර සම්බන්ධිත සේවා නාලිකා භාවිතා කිරීමේ අවසාන ඉලක්කය වන්නේ n සේවාලාභීන්ට එකවර සේවා සැපයීමෙන් ඉල්ලීම් සේවා කිරීමේ වේගය (තනි නාලිකා පද්ධතියකට සාපේක්ෂව) වැඩි කිරීමයි. අසමත්වීම් සහිත බහු-නාලිකා පෝලිම් පද්ධතියක රාජ්‍ය ප්‍රස්ථාරය රූප සටහන 4 හි පෙන්වා ඇත.

රූපය 4. අසාර්ථක වූ බහු නාලිකා QS හි රාජ්ය ප්රස්ථාරය

S 0 - සියලුම නාලිකා නොමිලේ;

S 1 - එක් නාලිකාවක් අල්ලාගෙන ඇත, ඉතිරිය නොමිලේ;

S k - හරියටම k නාලිකා අල්ලාගෙන ඇත, ඉතිරිය නොමිලේ;

S n - සියලුම n නාලිකා වාඩිලාගෙන ඇත, ඉතිරිය නොමිලේ.

P 0 , ... , P k , ... P n පද්ධති අවස්ථා වල සම්භාවිතාවන් සඳහා Kolmogorov ගේ සමීකරණ පහත දැක්වෙන ආකාරය ඇත:

පද්ධතිය විසඳීම සඳහා මූලික කොන්දේසි වනුයේ:

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0.

පද්ධතියේ ස්ථාවර විසඳුමට පෝරමය ඇත:

P k (3.5.1) සම්භාවිතා ගණනය කිරීමේ සූත්‍ර Erlang සූත්‍ර ලෙස හැඳින්වේ.

ස්ථාවර මාදිලියක අසාර්ථකත්වයන් සහිත බහු-නාලිකා QS ක්‍රියාකාරිත්වයේ සම්භාවිතා ලක්ෂණ අපි තීරණය කරමු:

1) අසාර්ථක වීමේ සම්භාවිතාව:

සියලුම n නාලිකා කාර්යබහුල වේලාවක ඉල්ලීමක් පැමිණියහොත් එය ප්‍රතික්ෂේප වන බැවිනි. P විවෘත අගය, එන ප්‍රවාහයට සේවා සැපයීමේ සම්පූර්ණත්වය සංලක්ෂිත කරයි;

2) සේවාව සඳහා ඉල්ලීම පිළිගැනීමේ සම්භාවිතාව (එය q පද්ධතියේ සාපේක්ෂ ධාරිතාව ද වේ) P එකකට විවෘත කරයි:

3) නිරපේක්ෂ ප්‍රතිදානය

4) සේවාව () විසින් අල්ලාගෙන සිටින සාමාන්‍ය නාලිකා සංඛ්‍යාව පහත පරිදි වේ:

අගය QS පැටවීමේ මට්ටම සංලක්ෂිත කරයි.

කාර්යයන්පාඩම 2 සඳහා

1. එක් නාලිකාවක් සහිත සන්නිවේදන ශාඛාවකට තත්පරයකට l = 0.08 පණිවිඩ තීව්‍රතාවයකින් සරලතම පණිවිඩ ප්‍රවාහය ලැබේ. සම්ප්රේෂණ කාලය එක්ස්ප් නීතියට අනුව බෙදා හරිනු ලැබේ. µ=0.1 තීව්‍රතාවයකින් එක් පණිවිඩයක සේවය සිදුවේ. සේවා සපයන නාලිකාව කලින් ලැබුණු පණිවිඩයක් සම්ප්‍රේෂණය කිරීමේදී කාර්යබහුල වන අවස්ථා වලදී පැමිණෙන පණිවිඩ සම්ප්‍රේෂණ අසාර්ථක වීමක් ලබයි.

කෝෆ්. සාපේක්ෂ නාලිකා භාරය (නාලිකා පදිංචි වීමේ සම්භාවිතාව)

P පණිවිඩයක් ලැබීමට අසමත් වීමේ සම්භාවිතාව ප්‍රතික්ෂේප කරයි

Q internode ශාඛාවේ සාපේක්ෂ ධාරිතාව

සහ සන්නිවේදන ශාඛාවේ නිරපේක්ෂ කාර්ය සාධනය.

2. සන්නිවේදන ශාඛාව එක් නාලිකාවක් ඇති අතර සෑම තත්පර 10 කට වරක් පණිවිඩ ලැබේ. එක් පණිවිඩයක් සඳහා සේවා කාලය තත්පර 5 කි. පණිවිඩ සම්ප්‍රේෂණ කාලය ඝාතීය නීතියකට අනුව බෙදා හරිනු ලැබේ. නාලිකාව කාර්යබහුල වන විට පැමිණෙන පණිවිඩ සේවාව ප්‍රතික්ෂේප කරයි.

නිර්වචනය කරන්න

Rzan - සන්නිවේදන නාලිකා පදිංචි වීමේ සම්භාවිතාව (සාපේක්ෂ බර සාධකය)

Q - සාපේක්ෂ ප්‍රතිදානය

A - සන්නිවේදන ශාඛාවේ නිරපේක්ෂ ධාරිතාව

4. ද්විතියික සන්නිවේදන ජාලයේ අභ්යන්තර ශාඛාව n = 4 නාලිකා ඇත. සන්නිවේදන ශාඛා නාලිකා හරහා සම්ප්‍රේෂණය සඳහා පැමිණෙන පණිවිඩ ප්‍රවාහයේ තීව්‍රතාවය = තත්පරයකට පණිවිඩ 8 කි. එක් පණිවිඩයක සාමාන්‍ය සම්ප්‍රේෂණ කාලය t = තත්පර 0.1 කි. සියලුම n නාලිකා කාර්යබහුල වන අවස්ථාවක පැමිණෙන පණිවිඩයකට සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්‍රේෂණ දෝෂයක් ලැබේ. SMO හි ලක්ෂණ සොයා ගන්න:

පාඩම 3

පොරොත්තු සහිත තනි නාලිකා පද්ධතිය

අපි දැන් බලා සිටීම සමඟ තනි නාලිකා QS සලකා බලමු. පෝලිම් පද්ධතියට එක් නාලිකාවක් ඇත. ලැබෙන සේවා ඉල්ලීම් ප්‍රවාහය තීව්‍රතාවයෙන් යුත් සරලම ප්‍රවාහයයි. සේවා ප්රවාහයේ තීව්රතාවය සමාන වේ (එනම්, සාමාන්යයෙන්, අඛණ්ඩව කාර්යබහුල නාලිකාවක් සේවා ඉල්ලීම් නිකුත් කරනු ඇත). සේවා කාලය ඝාතීය බෙදා හැරීමේ නීතියට යටත්ව අහඹු විචල්‍යයකි. සේවා ප්‍රවාහය යනු සිදුවීම්වල සරලම විෂ ප්‍රවාහයයි. නාලිකාව කාර්යබහුල වන විට ලැබුණු ඉල්ලීමක් පෝලිම්වල තබා සේවය සඳහා බලා සිටී. මෙම QS ආකෘති නිර්මාණයේ බහුලව දක්නට ලැබේ. එක් උපාධියක් හෝ තවත් ආසන්න වශයෙන්, එය දේශීය පරිගණක ජාලයක (LAN) ඕනෑම නෝඩයක් පාහේ අනුකරණය කිරීමට භාවිතා කළ හැක.

සේවා පද්ධතියේ ආදානයට කොපමණ ඉල්ලීම් පැමිණියද, මෙම පද්ධතිය (පෝලිම් + සේවාලාභීන්ට සේවය කරනු ලැබේ) යැයි අපි උපකල්පනය කරමු. බැහැ N-අවශ්‍යතා (අයදුම්පත්) වලට වඩා වැඩි ප්‍රමාණයකට ඉඩ සැලසීම, එනම් රඳවා නොගත් පාරිභෝගිකයින්ට වෙනත් තැනක සේවය කිරීමට බල කෙරේ. පද්ධතිය M/M/1/N. අවසාන වශයෙන්, මූලාශ්‍ර උත්පාදන සේවා ඉල්ලීම්වලට අසීමිත (අසීමිත විශාල) ධාරිතාවක් ඇත. මෙම අවස්ථාවෙහි QS හි රාජ්‍ය ප්‍රස්ථාරයේ රූප සටහන 3 හි පෙන්වා ඇති පෝරමය ඇත

රූපය 3. තනි නාලිකාවක QS හි රාජ්‍ය ප්‍රස්ථාරය බලා සිටීම (මරණය සහ ප්‍රජනන යෝජනා ක්‍රමය)

QS ප්‍රාන්තවලට පහත අර්ථකථන ඇත:

S 0 - "නාලිකාව නිදහස්";

S 1 - "නාලිකාව කාර්යබහුල" (පෝලිමක් නැත);

S 2 - "නාලිකාව කාර්යබහුල" (එක් ඉල්ලීමක් පෝලිමේ ඇත);

S n - "නාලිකාව කාර්යබහුල" (n -1 යෙදුම් පෝලිමේ ඇත);

S N - "නාලිකාව කාර්යබහුලයි" (N - 1 යෙදුම් පෝලිමේ ඇත).

මෙම පද්ධතියේ ස්ථාවර ක්‍රියාවලිය පහත වීජීය සමීකරණ පද්ධතිය මගින් විස්තර කෙරේ:

එහිදී p=load සාධකය

n - රාජ්ය අංකය.

අපගේ QS ආකෘතිය සඳහා ඉහත සමීකරණ පද්ධතියට විසඳුමේ ආකෘතිය ඇත:

සීමිත පෝලිම් දිගක් සහිත QS සඳහා ආරම්භක සම්භාවිතා අගය

අනන්ත පෝලිමක් සහිත QS සඳහා Н =? :

P 0 =1- s (3.4.7)

(N - 1) නොඉක්මවිය හැකි පෝලිමේ දිග සීමාවක් හඳුන්වා දීමෙන් සේවා පද්ධතියට ඇතුළත් කරන ලද අයදුම්පත් සංඛ්‍යාව පාලනය වන බැවින්, දී ඇති QS සඳහා නිශ්චලතා කොන්දේසිය සපුරාලීම අවශ්‍ය නොවන බව සටහන් කළ යුතුය. , සහ ආදාන ප්‍රවාහයේ තීව්‍රතාවයන් අතර අනුපාතය මගින් නොවේ, එනම් c = l/m අනුපාතය නොවේ.

ඉහත සලකා බැලූ තනි නාලිකා පද්ධතිය මෙන් නොව, අසීමිත පෝලිමක් සහිතව, මෙම අවස්ථාවෙහිදී, පැටවුම් සාධකය c හි ඕනෑම සීමිත අගයක් සඳහා ඉල්ලීම් ගණනක ස්ථාවර බෙදාහැරීමක් පවතී.

තනි නාලිකාවක QS හි ලක්ෂණ සහ (N - 1) (M/M/1/N) ට සමාන සීමිත පෝලිම් දිගක් මෙන්ම අසීමිත ධාරිතාවක් සහිත බෆරයක් සහිත තනි නාලිකා QS සඳහා ලක්ෂණ තීරණය කරමු. (M/M/1/?). අනන්ත පෝලිමක් සහිත QS සඳහා, කොන්දේසිය<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) අයදුම්පත්‍රයක් සේවය කිරීම ප්‍රතික්ෂේප කිරීමේ සම්භාවිතාව:

ඉල්ලීම් අහිමි විය හැකි පද්ධතිවල වැදගත්ම ලක්ෂණයක් වන්නේ අත්තනෝමතික ඉල්ලීමක් අහිමි වීමේ සම්භාවිතාව P අහිමි වීමයි. මෙම අවස්ථාවෙහිදී, අත්තනෝමතික ඉල්ලීමක් අහිමි වීමේ සම්භාවිතාව අත්තනෝමතික මොහොතක සියලු පොරොත්තු ස්ථාන අල්ලාගෙන සිටීමේ සම්භාවිතාව සමග සමපාත වේ, i.e. k = P N වෙතින් P සූත්‍රය වලංගු වේ

2) සාපේක්ෂ පද්ධති ධාරිතාව:

අසීමිත සමග SMO සඳහාth පෝලිම q =1,නිසා සියලුම ඉල්ලීම් සේවා සපයනු ලැබේ

3) නිරපේක්ෂ ප්‍රතිදානය:

4) පද්ධතියේ සාමාන්‍ය යෙදුම් ගණන:

අසීමිත පෝලිමක් සහිත L S

5) යෙදුමක් පද්ධතියේ පවතින සාමාන්‍ය කාලය:

අසීමිත පෝලිම් සඳහා

6) සේවාලාභියෙකුගේ (අයදුම්පත) පෝලිමේ රැඳී සිටින සාමාන්ය කාලය:

අසීමිත පෝලිමක් සමඟ

7) පෝලිමේ ඇති සාමාන්‍ය යෙදුම් ගණන (සේවාලාභීන්) (පෝලිමේ දිග):

අසීමිත පෝලිමක් සමඟ

T och පෝලිමේ සාමාන්‍ය පොරොත්තු කාලය සඳහා ප්‍රකාශන සහ L och පෝලිමේ සාමාන්‍ය දිග සඳහා වන සූත්‍රය මෙන්ම T S පද්ධතියේ ඉල්ලීම්වල සාමාන්‍ය පදිංචි කාලය සහ L S පද්ධතියේ සාමාන්‍ය ඉල්ලීම් සංඛ්‍යාව සංසන්දනය කිරීම, අපි එය දකිනවා

L och =l*T och L s =l* T s

සලකා බලනු ලබන M/M/1 පද්ධතියට වඩා සාමාන්‍ය බොහෝ පෝලිම් පද්ධති සඳහා මෙම සූත්‍ර වලංගු වන අතර Little's formula ලෙස හඳුන්වනු ලබන බව සලකන්න. මෙම සූත්‍රවල ප්‍රායෝගික වැදගත්කම නම්, L och සහ L s යන අගයන්හි දන්නා අගයක් සමඟ T och සහ T s හි අගයන් කෙලින්ම ගණනය කිරීමේ අවශ්‍යතාවය සහ අනෙක් අතට ඒවා ඉවත් කිරීමයි.

තනි නාලිකා කාර්යයන් SMOඅපේක්ෂාවෙන්, සමගබලා සිටීම සහසීමිත පෝලිම් දිග

1. අසීමිත පෝලිම් ගබඩාවක් සහිත තනි පේළියක් QS ලබා දී ඇත. සෑම t = තත්පර 14 කට වරක් අයදුම්පත් ලැබේ. එක් පණිවිඩයක සාමාන්‍ය සම්ප්‍රේෂණ කාලය t=තත්පර 10 කි. සේවා සපයන නාලිකාව කාර්යබහුල වන අවස්ථා වලදී පැමිණෙන පණිවිඩ සේවා කිරීම ආරම්භ කිරීමට පෙර පෝලිමෙන් ඉවත් නොවී පෝලිමේ ලැබේ.

පහත කාර්ය සාධන දර්ශක තීරණය කරන්න:

2. එක් නාලිකාවක් සහ m=3 පොරොත්තු පණිවිඩ (N-1=m) සඳහා පෝලිම් ගබඩාවක් ඇති internode සන්නිවේදන ශාඛාව, l=5 පණිවිඩ තීව්‍රතාවයකින් සරලම පණිවිඩ ප්‍රවාහය ලබා ගනී. තත්පර කිහිපයකින් පණිවිඩ සම්ප්‍රේෂණ කාලය ඝාතීය නීතියකට අනුව බෙදා හරිනු ලැබේ. එක් පණිවිඩයක සාමාන්‍ය සම්ප්‍රේෂණ කාලය තත්පර 0.1 කි. සේවා සපයන නාලිකාව කලින් ලැබුණු පණිවිඩයක් සම්ප්‍රේෂණය කිරීමේදී කාර්යබහුල වන විට සහ ධාවකයේ නිදහස් ඉඩක් නොමැති අවස්ථාවලදී පැමිණෙන පණිවිඩ ප්‍රතික්ෂේප කරනු ලැබේ.

P විවෘත - පණිවිඩයක් ලැබීමට අසමත් වීමේ සම්භාවිතාව

L පද්ධතිය - පෝලිමේ සහ සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්රේෂණය කරන ලද සාමාන්ය මුළු පණිවිඩ සංඛ්යාව

T och - සම්ප්‍රේෂණය ආරම්භ වීමට පෙර පණිවිඩයක් පෝලිමේ පවතින සාමාන්‍ය කාලය

T syst - පද්ධතිය තුළ පණිවිඩයක් ඉතිරිව ඇති සාමාන්‍ය මුළු කාලය, එය පෝලිමේ සාමාන්‍ය පොරොත්තු කාලය සහ සාමාන්‍ය සම්ප්‍රේෂණ කාලයෙහි එකතුවයි.

Q - සාපේක්ෂ ප්‍රතිදානය

A - නිරපේක්ෂ ප්‍රතිදානය

3. m = 4 (N-1=4) පොරොත්තු පණිවිඩ සඳහා එක් නාලිකාවක් සහ පෝලිම් ගබඩාවක් ඇති ද්විතීයික සන්නිවේදන ජාලයේ internode ශාඛාව, තීව්‍රතාවය = තත්පරයට පණිවිඩ 8 ක් සහිත සරලම පණිවිඩ ප්‍රවාහය ලබා ගනී. පණිවිඩ සම්ප්‍රේෂණ කාලය ඝාතීය නීතියකට අනුව බෙදා හරිනු ලැබේ. එක් පණිවිඩයක සාමාන්‍ය සම්ප්‍රේෂණ කාලය t = 0.1 තත්පර වේ. සේවා සපයන නාලිකාව කලින් ලැබුණු පණිවිඩයක් සම්ප්‍රේෂණය කිරීමේදී කාර්යබහුල වන විට සහ ධාවකයේ නිදහස් ඉඩක් නොමැති අවස්ථාවලදී පැමිණෙන පණිවිඩ පෝලිමෙන් ප්‍රතික්ෂේප වේ.

P විවෘත - internode ශාඛාවේ සන්නිවේදන නාලිකාව හරහා සම්ප්රේෂණය සඳහා පණිවිඩයක් ලැබීමට අසමත් වීමේ සම්භාවිතාව;

L och - පෝලිමේ ද්විතියික ජාලයේ සන්නිවේදන ශාඛාව වෙත පෝලිමේ සාමාන්ය පණිවිඩ සංඛ්යාව;

L පද්ධතිය - පෝලිමේ සහ ද්විතියික ජාලයේ සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්රේෂණය කරන ලද සාමාන්ය මුළු පණිවිඩ සංඛ්යාව;

T och - සම්ප්‍රේෂණය ආරම්භ වීමට පෙර පණිවිඩයක් පෝලිමේ පවතින සාමාන්‍ය කාලය;

Rzan - සන්නිවේදන නාලිකාව කාර්යබහුල වීමේ සම්භාවිතාව (සාපේක්ෂ නාලිකා භාර සංගුණකය);

Q යනු අභ්යන්තර ශාඛාවේ සාපේක්ෂ ධාරිතාවය;

A යනු අභ්යන්තර ශාඛාවේ නිරපේක්ෂ ධාරිතාවය;

4. එක් නාලිකාවක් සහ m=2 පොරොත්තු පණිවිඩ සඳහා පෝලිම් ගබඩාවක් ඇති internode සන්නිවේදන ශාඛාව, l=4 පණිවිඩ තීව්‍රතාවයකින් සරලම පණිවිඩ ප්‍රවාහය ලබා ගනී. තත්පර කිහිපයකින් පණිවිඩ සම්ප්රේෂණය කිරීමේ කාලය ඝාතීය නීතියක් අනුව බෙදා හරිනු ලැබේ. එක් පණිවිඩයක සාමාන්‍ය සම්ප්‍රේෂණ කාලය තත්පර 0.1 කි. සේවා සපයන නාලිකාව කලින් ලැබුණු පණිවිඩයක් සම්ප්‍රේෂණය කිරීමේදී කාර්යබහුල වන විට සහ ධාවකයේ නිදහස් ඉඩක් නොමැති අවස්ථාවලදී පැමිණෙන පණිවිඩ ප්‍රතික්ෂේප කරනු ලැබේ.

සන්නිවේදන ශාඛාවේ පහත සඳහන් කාර්ය සාධන දර්ශක නිර්ණය කරන්න:

P විවෘත - පණිවිඩයක් ලැබීමට අසමත් වීමේ සම්භාවිතාව

L och - සන්නිවේදන ශාඛාව වෙත පෝලිමේ සාමාන්ය පණිවිඩ සංඛ්යාව

L පද්ධතිය - පෝලිමේ සහ සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්රේෂණය කරන ලද සාමාන්ය මුළු පණිවිඩ සංඛ්යාව

T och - සම්ප්‍රේෂණය ආරම්භ වීමට පෙර පණිවිඩයක් පෝලිමේ පවතින සාමාන්‍ය කාලය

T syst - පද්ධතිය තුළ පණිවිඩයක් ඉතිරිව ඇති සාමාන්‍ය මුළු කාලය, එය පෝලිමේ සාමාන්‍ය පොරොත්තු කාලය සහ සාමාන්‍ය සම්ප්‍රේෂණ කාලයෙහි එකතුවයි.

Rzan - සන්නිවේදන නාලිකා පදිංචි වීමේ සම්භාවිතාව (සාපේක්ෂ නාලිකා භාර සංගුණකය c)

Q - සාපේක්ෂ ප්‍රතිදානය

A - නිරපේක්ෂ ප්‍රතිදානය

5. එක් නාලිකාවක් සහ පොරොත්තු පණිවිඩවල අසීමිත වෙළුම් ගබඩා පෝලිමක් ඇති ද්විතීයික සන්නිවේදන ජාලයේ internode ශාඛාව, තත්පරයට l = 0.06 පණිවිඩ තීව්‍රතාවයකින් යුත් සරලම පණිවිඩ ප්‍රවාහය ලබා ගනී. එක් පණිවිඩයක සාමාන්‍ය සම්ප්‍රේෂණ කාලය t = තත්පර 10 කි. සන්නිවේදන නාලිකාව කාර්යබහුල වන අවස්ථා වලදී පැමිණෙන පණිවිඩ පෝලිමක ලැබෙන අතර සේවාව ආරම්භ වන තුරු එය අත්හැර නොයන්න.

ද්විතියික ජාල සන්නිවේදන ශාඛාවේ පහත සඳහන් කාර්ය සාධන දර්ශක නිර්ණය කරන්න:

L och - සන්නිවේදන ශාඛාව වෙත පෝලිමේ සාමාන්ය පණිවිඩ සංඛ්යාව;

L පද්ධතිය - පෝලිමේ සහ සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්රේෂණය කරන ලද සාමාන්ය මුළු පණිවිඩ සංඛ්යාව;

T och - පණිවිඩයක් පෝලිමේ රැඳී සිටින සාමාන්ය කාලය;

T syst යනු පද්ධතියේ පණිවිඩයක් ඉතිරිව ඇති සාමාන්‍ය මුළු කාලයයි, එය පෝලිමේ සාමාන්‍ය පොරොත්තු කාලය සහ සාමාන්‍ය සම්ප්‍රේෂණ කාලයෙහි එකතුවයි;

Rzan යනු සන්නිවේදන නාලිකාව කාර්යබහුල වීමේ සම්භාවිතාවයි (සාපේක්ෂ නාලිකා භාර සාධකය);

Q - අභ්යන්තර ශාඛාවේ සාපේක්ෂ ධාරිතාව;

A - අභ්යන්තර ශාඛාවේ නිරපේක්ෂ ධාරිතාව

6. අසීමිත පෝලිම් ගබඩාවක් සහිත තනි පේළියක් QS ලබා දී ඇත. සෑම t = තත්පර 13 කට වරක් අයදුම්පත් ලැබේ. එක් පණිවිඩයක් සම්ප්‍රේෂණය කිරීමට සාමාන්‍ය කාලය

t=තත්පර 10. සේවා සපයන නාලිකාව කාර්යබහුල වන අවස්ථා වලදී පැමිණෙන පණිවිඩ සේවා කිරීම ආරම්භ කිරීමට පෙර පෝලිමෙන් ඉවත් නොවී පෝලිමේ ලැබේ.

පහත කාර්ය සාධන දර්ශක තීරණය කරන්න:

L och - පෝලිමේ ඇති සාමාන්‍ය පණිවිඩ සංඛ්‍යාව

L පද්ධතිය - පෝලිමේ සහ සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්රේෂණය කරන ලද සාමාන්ය මුළු පණිවිඩ සංඛ්යාව

T och - සම්ප්‍රේෂණය ආරම්භ වීමට පෙර පණිවිඩයක් පෝලිමේ පවතින සාමාන්‍ය කාලය

T syst - පද්ධතිය තුළ පණිවිඩයක් ඉතිරිව ඇති සාමාන්‍ය මුළු කාලය, එය පෝලිමේ සාමාන්‍ය පොරොත්තු කාලය සහ සාමාන්‍ය සම්ප්‍රේෂණ කාලයෙහි එකතුවයි.

Rzan - පදිංචි වීමේ සම්භාවිතාව (සාපේක්ෂ නාලිකා භාර සංගුණකය c)

Q - සාපේක්ෂ ප්‍රතිදානය

A - නිරපේක්ෂ ප්‍රතිදානය

7. විශේෂිත රෝග විනිශ්චය තනතුර තනි නාලිකා QS වේ. රෝග විනිශ්චය බලා සිටින මෝටර් රථ සඳහා වාහන නැවැත්වීමේ ස්ථාන ගණන සීමිත වන අතර 3 [(N - 1) = 3] ට සමාන වේ. සියලුම වාහන නැවැත්වීමේ ස්ථාන අල්ලාගෙන තිබේ නම්, එනම්, පෝලිමේ දැනටමත් මෝටර් රථ තුනක් තිබේ නම්, රෝග විනිශ්චය සඳහා පැමිණෙන ඊළඟ මෝටර් රථය සේවය සඳහා පෝලිමේ තබා නැත. රෝග විනිශ්චය සඳහා පැමිණෙන මෝටර් රථ ප්රවාහය පොයිසන්ගේ නීතියට අනුව බෙදා හරින අතර එහි තීව්රතාවය = 0.85 (පැයකට මෝටර් රථ) ඇත. වාහනයේ රෝග විනිශ්චය කාලය ඝාතීය නීතියකට අනුව බෙදා හරින අතර සාමාන්‍යයෙන් පැය 1.05 කි.

ස්ථාවර මාදිලියේ ක්‍රියාත්මක වන රෝග විනිශ්චය මධ්‍යස්ථානයක සම්භාවිතා ලක්ෂණ තීරණය කිරීම අවශ්‍ය වේ: P 0 , P 1 , P 2 , P 3 , P 4 , P open , q, A, L och, L sys, T och, T sys

පාඩම 4

බලා සිටීම, රැඳී සිටීම සහ සීමිත පෝලිම් දිග සමඟ බහු-නාලිකා QS

බලා සිටීම සමඟ බහු නාලිකා පෝලිම් පද්ධතියක් සලකා බලමු. අන්තර්ක්‍රියාකාරී මාදිලියේ ක්‍රියාත්මක වන LAN ග්‍රාහක පර්යන්තවල කණ්ඩායම් ආකෘති නිර්මාණය කිරීමේදී මෙම වර්ගයේ QS බොහෝ විට භාවිතා වේ. පෝලිම් ක්‍රියාවලිය පහත ලක්ෂණ වලින් සංලක්ෂිත වේ: ආදාන සහ ප්‍රතිදාන ප්‍රවාහයන් තීව්‍රතාවයෙන් යුත් Poisson සහ පිළිවෙලින්; n සේවාදායකයින්ට වඩා සමාන්තරව සේවය කළ නොහැක. පද්ධතියට සේවා නාලිකා ඇත. එක් සේවාලාභියෙකු සඳහා සාමාන්‍ය සේවා කාලය එක් එක් නාලිකාව සඳහා 1/m වේ. මෙම ක්‍රමය මරණය හා ප්‍රජනන ක්‍රියාවලියට ද යොමු කරයි.

c=l/nm - ලැබෙන ප්‍රවාහයේ තීව්‍රතාවයේ මුළු සේවා තීව්‍රතාවයට අනුපාතය, පද්ධති පැටවීමේ සාධකය වේ

(සමග<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

P 0 යනු අසීමිත පෝලිමක් සහිත සියලුම නාලිකාවල නිදහස් තත්වයේ සම්භාවිතාව වන අතර, k යනු ඉල්ලීම් ගණනයි.

අපි c = l / m ගන්නේ නම්, P 0 අසීමිත පෝලිමක් සඳහා තීරණය කළ හැකිය:

සීමිත පෝලිමක් සඳහා:

m යනු පෝලිම් දිග වේ

අසීමිත පෝලිමක් සමඟ:

සාපේක්ෂ ධාරිතාව q=1,

නිරපේක්ෂ ධාරිතාව A=l,

වාඩිලාගෙන සිටින නාලිකාවල සාමාන්‍ය සංඛ්‍යාව Z=A/m

සීමිත පෝලිමක් සහිතව

1 ද්විතියික සන්නිවේදන ජාලයේ internode ශාඛාව n = 4 නාලිකා ඇත. සන්නිවේදන ශාඛා නාලිකා හරහා සම්ප්‍රේෂණය සඳහා පැමිණෙන පණිවිඩ ප්‍රවාහයේ තීව්‍රතාවය = තත්පරයකට පණිවිඩ 8 කි. සෑම සන්නිවේදන නාලිකාවකින්ම එක් පණිවිඩයක් සම්ප්‍රේෂණය කිරීම සඳහා සාමාන්‍ය කාලය t = 0.1 t/n = තත්පර 0.025 කි. පෝලිමේ පණිවිඩ සඳහා රැඳී සිටින කාලය අසීමිතයි. SMO හි ලක්ෂණ සොයා ගන්න:

P විවෘත - පණිවිඩ සම්ප්රේෂණය අසාර්ථක වීමේ සම්භාවිතාව;

Q යනු සන්නිවේදන ශාඛාවේ සාපේක්ෂ ධාරිතාවය;

A යනු සන්නිවේදන ශාඛාවේ නිරපේක්ෂ ප්‍රතිදානයයි;

Z - වාඩිලාගෙන සිටින නාලිකා සාමාන්ය සංඛ්යාව;

L och - පෝලිමේ සාමාන්ය පණිවිඩ සංඛ්යාව;

T = සාමාන්ය පොරොත්තු කාලය;

T syst - පෝලිමේ රැඳී සිටින පණිවිඩවල සාමාන්‍ය මුළු කාලය සහ සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්‍රේෂණය වේ.

2. තනතුරු තුනක් (නාලිකා) සහිත බලාගාරයේ යාන්ත්රික වැඩමුළුව කුඩා යාන්ත්රිකකරණයේ අලුත්වැඩියා කටයුතු සිදු කරයි. වැඩමුළුවට පැමිණෙන දෝෂ සහිත යාන්ත්රණ ප්රවාහය Poisson වන අතර දිනකට තීව්රතාවය = 2.5 යාන්ත්රණ ඇත, එක් යාන්ත්රණයක් සඳහා සාමාන්ය අලුත්වැඩියා කාලය ඝාතීය නීතියට අනුව බෙදා හරින අතර එය = 0.5 දිනට සමාන වේ. බලාගාරයේ වෙනත් වැඩමුළුවක් නොමැති බව උපකල්පනය කරමු, එබැවින් වැඩමුළුව ඉදිරිපිට යාන්ත්‍රණ පෝලිම අසීමිත ලෙස වර්ධනය විය හැකිය. පද්ධතියේ සම්භාවිතා ලක්ෂණ වල පහත සඳහන් සීමාකාරී අගයන් ගණනය කිරීම අවශ්ය වේ:

පද්ධති අවස්ථා වල සම්භාවිතාව;

සේවා සඳහා පෝලිමේ සාමාන්ය අයදුම්පත් සංඛ්යාව;

පද්ධතියේ සාමාන්ය යෙදුම් සංඛ්යාව;

යෙදුමක් පෝලිමේ පවතින සාමාන්‍ය කාලය;

යෙදුමක් පද්ධතිය තුළ රැඳී සිටීමේ සාමාන්‍ය කාලය.

3. ද්විතියික සන්නිවේදන ජාලයේ internode ශාඛාව n=3 නාලිකා ඇත. සන්නිවේදන ශාඛා නාලිකා හරහා සම්ප්‍රේෂණය සඳහා පැමිණෙන පණිවිඩ ප්‍රවාහය තත්පරයකට l = පණිවිඩ 5 ක තීව්‍රතාවයක් ඇත. එක් පණිවිඩයක සාමාන්‍ය සම්ප්‍රේෂණ කාලය t=0.1, t/n=0.033 තත්ත්පර සම්ප්‍රේෂණය කිරීමට බලාපොරොත්තු වන පණිවිඩවල පෝලිම් ගබඩාවේ m= පණිවිඩ 2ක් දක්වා අඩංගු විය හැක. පෝලිමේ සියලුම ස්ථාන අල්ලාගෙන සිටින අවස්ථාවක පැමිණෙන පණිවිඩයකට සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්‍රේෂණ දෝෂයක් ලැබේ. QS හි ලක්ෂණ සොයන්න: P විවෘත - පණිවිඩ සම්ප්‍රේෂණ අසාර්ථක වීමේ සම්භාවිතාව, Q - සාපේක්ෂ ප්‍රතිදානය, A - නිරපේක්ෂ ප්‍රතිදානය, Z - සාමාන්‍ය වාඩිලාගෙන සිටින නාලිකා සංඛ්‍යාව, L och - පෝලිමේ සාමාන්‍ය පණිවිඩ සංඛ්‍යාව, T එසේ - සාමාන්‍ය රැඳී සිටීම කාලය, ටී පද්ධතිය - පණිවිඩයක් පෝලිමේ පවතින අතර සන්නිවේදන ශාඛාව ඔස්සේ සම්ප්‍රේෂණය වන සාමාන්‍ය මුළු කාලය.

පාඩම 5

වසා දැමූ QS

සංවෘත පෝලිම් පද්ධතියක ආකෘතියක් වන මැෂින් ෆ්ලීට් සේවා ආකෘතියක් සලකා බලමු. මේ වන තෙක්, අපි සලකා බැලුවේ ලැබෙන ඉල්ලීම් ප්‍රවාහයේ තීව්‍රතාවය පද්ධතියේ තත්වය මත රඳා නොපවතින පෝලිම් පද්ධති පමණි. මෙම අවස්ථාවෙහිදී, ඉල්ලීම්වල මූලාශ්‍රය QS වෙතින් බාහිර වන අතර ඉල්ලීම් අසීමිත ප්‍රවාහයක් ජනනය කරයි. එය පද්ධතියේ තත්වය මත රඳා පවතින පෝලිම් පද්ධති සලකා බලමු, සහ අවශ්‍යතා මූලාශ්‍රය අභ්‍යන්තර වන අතර සීමිත ඉල්ලීම් ප්‍රවාහයක් ජනනය කරයි. උදාහරණයක් ලෙස, N යන්ත්‍ර වලින් සමන්විත යන්ත්‍ර උද්‍යානයක් R යාන්ත්‍රික කණ්ඩායමක් (N > R) විසින් සේවය කරනු ලබන අතර, සෑම යන්ත්‍රයක්ම සේවය කළ හැක්කේ එක් කාර්මිකයෙකුට පමණි. මෙහිදී යන්ත්‍ර යනු අවශ්‍යතා (සේවා සඳහා ඉල්ලීම්) මූලාශ්‍ර වන අතර යාන්ත්‍ර විද්‍යාව යනු සේවා නාලිකා වේ. දෝෂ සහිත යන්ත්‍රයක්, සේවා කිරීමෙන් පසු, එහි අපේක්ෂිත කාර්යය සඳහා භාවිතා කරන අතර සේවා අවශ්‍යතා සඳහා විභව මූලාශ්‍රයක් බවට පත්වේ. පැහැදිලිවම, තීව්‍රතාවය රඳා පවතින්නේ දැනට ක්‍රියාත්මක වන යන්ත්‍ර කීයක් (N - k) සහ කොපමණ යන්ත්‍ර ප්‍රමාණයක් සේවා සපයන්නේද හෝ සේවය බලාපොරොත්තුවෙන් සිටිනුයේද යන්න මතය (k). සලකා බලනු ලබන ආකෘතියේ, අවශ්‍යතා ප්‍රභවයේ ධාරිතාව සීමිත ලෙස සැලකිය යුතුය. ඉල්ලුම් ප්‍රවාහය පැමිණෙන්නේ සීමිත මෙහෙයුම් යන්ත්‍ර සංඛ්‍යාවකින් (N - k), අහඹු අවස්ථාවලදී බිඳවැටෙන අතර නඩත්තුව අවශ්‍ය වේ. තවද, (N - k) සිට සෑම යන්ත්‍රයක්ම ක්‍රියාත්මක වේ. අනෙකුත් වස්තූන් නොතකා X තීව්‍රතාවයෙන් යුතු අවශ්‍යතා වල Poisson ප්‍රවාහයක් උත්පාදනය කරයි, මුළු (සම්පූර්ණ) එන ප්‍රවාහයට තීව්‍රතාවයක් ඇත. අවම වශයෙන් එක් නාලිකාවක් නොමිලේ වන විට පද්ධතියට ඇතුළු වන ඉල්ලීමක් වහාම සකසනු ලැබේ. ඉල්ලීමක් මඟින් සියලුම නාලිකා වෙනත් ඉල්ලීම් සඳහා කාර්යබහුල බව සොයා ගන්නේ නම්, එය පද්ධතියෙන් ඉවත් නොවී, පෝලිමකට ගොස් එක් නාලිකාවක් නිදහස් වන තෙක් රැඳී සිටියි. මේ අනුව, සංවෘත පෝලිම් පද්ධතියක, පිටතට යන එකෙන් ලැබෙන අවශ්‍යතා ප්‍රවාහය සෑදී ඇත. S k පද්ධති තත්ත්වය සංලක්ෂිත වන්නේ සේවා කරන ලද මුළු ඉල්ලීම් සංඛ්‍යාව සහ පෝලිමේ k ට සමාන වේ. සලකා බලනු ලබන සංවෘත පද්ධතිය සඳහා, පැහැදිලිවම, k = 0, 1, 2, ... , N. තවද, පද්ධතිය S k රාජ්‍යයේ නම්, ක්‍රියාත්මක වන වස්තු ගණන (N - k) ට සමාන වේ. . යන්ත්‍රයකට ඉල්ලුමේ ප්‍රවාහයේ තීව්‍රතාවය නම්, එසේ නම්:

සංවෘත ලූප QS ස්ථායී ආකාරයෙන් ක්‍රියාත්මක වන ආකාරය විස්තර කරන වීජීය සමීකරණ පද්ධතිය පහත පරිදි වේ:

මෙම පද්ධතිය විසඳීම, අපි kth තත්වයේ සම්භාවිතාව සොයා ගනිමු:

P 0 හි අගය තීරණය වන්නේ P k, k = 0, 1, 2, ... , N සඳහා සූත්‍ර භාවිතයෙන් ලබාගත් ප්‍රතිඵල සාමාන්‍යකරණය කිරීමේ කොන්දේසියෙනි. අපි පද්ධතියේ පහත සම්භාවිතා ලක්ෂණ තීරණය කරමු:

සේවාව සඳහා පෝලිමේ ඇති සාමාන්‍ය ඉල්ලීම් ගණන:

පද්ධතියේ සාමාන්‍ය ඉල්ලීම් සංඛ්‍යාව (සේවය කිරීම සහ පෝලිම් තැබීම)

වැඩ නොමැතිකම හේතුවෙන් යාන්ත්රික (නාලිකා) සාමාන්ය සංඛ්යාව "නිෂ්ක්රීය"

පෝලිමේ සේවා කරන ලද වස්තුවේ (යන්ත්‍රයෙහි) උදාසීනතා අනුපාතය

පහසුකම් භාවිතා කිරීමේ අනුපාතය (යන්ත්‍ර)

සේවා නාලිකාවල අක්‍රීය කාල අනුපාතය (යාන්ත්‍ර විද්‍යාව)

සේවාව සඳහා සාමාන්‍ය පොරොත්තු කාලය (පෝලිමේ සේවය සඳහා රැඳී සිටින කාලය)

වසා දැමූ QS ගැටළුව

1. පුද්ගලික පරිගණක (PCs) දහයකට සේවා සැපයීමට සමාන ඵලදායිතාවයකින් යුත් ඉංජිනේරුවන් දෙදෙනෙකුට වෙන් කරමු. එක් පරිගණකයක අසමත්වීම් (අක්රිය) ප්රවාහය තීව්රතාවය සහිත Poisson = 0.2. පරිගණක නඩත්තු කාලය ඝාතීය නීතියට කීකරු වේ. එක් ඉංජිනේරුවෙකු විසින් එක් පරිගණකයකට සේවා සැපයීමේ සාමාන්‍ය කාලය: = පැය 1.25 කි. පහත සේවා සංවිධාන විකල්පයන් හැකි ය:

ඉංජිනේරුවන් දෙදෙනාම පරිගණක දහයටම සේවය කරයි, එබැවින් පරිගණකයක් අසමත් වුවහොත්, එය නොමිලේ ඉංජිනේරුවෙකු විසින් සේවය කරනු ලැබේ, මෙම අවස්ථාවේදී R = 2, N = 10;

එක් එක් ඉංජිනේරුවන් දෙදෙනා ඔහුට පවරා ඇති පළාත් සභා පහ බැගින් නඩත්තු කරයි. මෙම අවස්ථාවේදී R = 1, N = 5.

PC නඩත්තුව සංවිධානය කිරීම සඳහා හොඳම විකල්පය තෝරා ගැනීම අවශ්ය වේ.

P k: P 1 - P 10 ප්‍රාන්තවල සියලුම සම්භාවිතා තීරණය කිරීම අවශ්‍ය වේ, P k ගණනය කිරීමේ ප්‍රති results ල භාවිතා කරමින් අපි P 0 ගණනය කරන බව සැලකිල්ලට ගනිමු.

පාඩම 6

රථවාහන ගණනය කිරීම.

Teletraffic theory යනු පෝලිම් න්‍යායේ කොටසකි. ටෙලි ට්‍රැෆික් න්‍යායේ අඩිතාලම දැම්මේ ඩෙන්මාර්ක් විද්‍යාඥ ඒ.කේ. අර්ලන්ග්. ඔහුගේ කෘති 1909-1928 දී ප්රකාශයට පත් විය. අපි ටෙලිට්‍රැෆික් (TT) න්‍යායේ භාවිතා කරන වැදගත් නිර්වචන ලබා දෙමු. "රථවාහන" යන යෙදුම "දුරකථන භාරය" යන පදයට අනුරූප වේ. මෙය QS හි යෙදවුම් වෙත පැමිණෙන ඇමතුම්, ඉල්ලීම් සහ පණිවිඩ ගලායාම මගින් නිර්මාණය කරන ලද භාරයට යොමු කරයි. ගමනාගමන පරිමාව යනු විශ්ලේෂණය කරන ලද කාල පරිච්ෙඡ්දය තුළ මෙම සම්පත අත්පත් කර ගත් එක් හෝ තවත් සම්පතක් මග හැරුණු සම්පූර්ණ, අනුකලිත කාල පරතරයේ ප්‍රමාණයයි. වැඩ ඒකකයක් සම්පතක දෙවන රැකියාව ලෙස සැලකිය හැකිය. සමහර විට ඔබට පැයක වැඩ, සමහර විට තත්පර හෝ පැය කියවිය හැක. කෙසේ වෙතත්, ITU නිර්දේශ මගින් erlango-hours තුළ රථවාහන පරිමාවේ මානය ලබා දේ. එවැනි මිනුම් ඒකකයක අර්ථය තේරුම් ගැනීම සඳහා, අපි තවත් රථවාහන පරාමිතියක් සලකා බැලිය යුතුය - රථවාහන තීව්රතාව. මෙම අවස්ථාවෙහිදී, ඔවුන් බොහෝ විට යම් යම් සම්පත් සංචිතයක් (කට්ටලයක්) මත රථවාහන (භාරය) සාමාන්ය තීව්රතාව ගැන කතා කරයි. සෑම මොහොතකම t දී ඇති පරතරයකින් (t 1,t 2) සේවා ගමනාගමනයේ යෙදී සිටින දී ඇති කට්ටලයක සම්පත් සංඛ්‍යාව A(t) ට සමාන නම්, සාමාන්‍ය ගමනාගමන තීව්‍රතාවය වනු ඇත.

ගමනාගමන තීව්‍රතාවයේ අගය සංලක්ෂිත වන්නේ දී ඇති කාල පරතරයකදී ගමනාගමනයට සේවා සැපයීමෙන් සාමාන්‍ය සම්පත් සංඛ්‍යාව ලෙසිනි. බර තීව්රතාව මැනීමේ ඒකකය Erlang (1 Erl, 1 E), i.e. 1 Erlang යනු එක් සම්පතක පූර්ණ සේවා නියුක්තිය අවශ්‍ය වන එවැනි රථවාහන තීව්‍රතාවයකි, නැතහොත් වෙනත් වචන වලින් කිවහොත්, සම්පත එක් තත්පරයක තත්පරයක රැකියාවක් වටිනා කාර්යයක් ඉටු කරයි. ඇමරිකානු සාහිත්‍යයේ, ඔබට සමහර විට CCS-Centrum (හෝ සියයක්) ඇමතුම් දෙවන ලෙස හැඳින්වෙන තවත් මිනුම් ඒකකයක් සොයාගත හැකිය. CCS අංකය පැයකට තත්පර 100 ක පරතරයකින් සේවාදායක වාඩිලාගැනීමේ කාලය පිළිබිඹු කරයි. CCS හි මනිනු ලබන තීව්‍රතාවය 36CCS=1 Erl සූත්‍රය භාවිතයෙන් Erlang බවට පරිවර්තනය කළ හැක.

එක් මූලාශ්‍රයකින් ජනනය වන සහ පැය-රැකියාවන්හි ප්‍රකාශිත ගමනාගමනය යම් කාල පරතරයක් සඳහා C ඇමතුම් උත්සාහ ගණනේ ගුණිතයට සමාන වේ T සහ එක් උත්සාහයක සාමාන්‍ය කාලසීමාව t: y = c t (h-z). ගමනාගමනය විවිධ ආකාර තුනකින් ගණනය කළ හැකිය:

1) පැයකට c ඇමතුම් ගණන 1800 ට ඉඩ දෙන්න, සහ සැසියේ සාමාන්‍ය කාලය t = විනාඩි 3, පසුව Y = 1800 ඇමතුම්. /h. 0.05 h = 90 අර්ල්;

2) යම් බණ්ඩලයක නිමැවුම්වල සියලුම n වෘත්තීන්හි කාලසීමාවන් T කාලය තුළ ස්ථාවර කිරීමට ඉඩ දෙන්න, එවිට ගමනාගමනය පහත පරිදි තීරණය වේ:

3) නිරීක්ෂණ ප්‍රතිඵල මත පදනම්ව T කාලය තුළ යම්කිසි කදම්භයක සමකාලීන ප්‍රතිදානයන් සංඛ්‍යාව නිරීක්ෂණය කිරීමට ඉඩ දෙන්න, x(t) කාලයෙහි පියවර ශ්‍රිතයක් ගොඩනගා ඇත (රූපය 8).

රූපය 8. එකවර වාඩිලාගත් කදම්භ නිමැවුම් වල සාම්පල

T කාලය තුළ ගමනාගමනය එම කාලය තුළ x(t) හි සාමාන්‍ය අගය ලෙස ඇස්තමේන්තු කළ හැක:

මෙහි n යනු එකවර අත්පත් කරගත් නිමැවුම්වල සාම්පල ගණනයි. අගය Y යනු T කාලය තුළ එකවර භාවිතා කරන ලද කදම්භ නිමැවුම් වල සාමාන්‍ය සංඛ්‍යාවයි.

රථවාහන උච්චාවචනයන්. ද්විතියික දුරකථන ජාල වල ගමනාගමනය කාලයත් සමඟ සැලකිය යුතු ලෙස උච්චාවචනය වේ. වැඩ කරන දිනය තුළ, රථවාහන වක්‍රය මුදුන් දෙකක් හෝ තුනක් ඇත (රූපය 9).

රූපය 9. දිවා කාලයේ රථවාහන උච්චාවචනයන්

දීර්ඝ කාලයක් තිස්සේ ගමනාගමනය නිරීක්ෂණය කරන දවසේ පැය වඩාත් වැදගත් වන්නේ කාර්යබහුලම පැය (BHH) ලෙසිනි. සීඑන්එන් හි ගමනාගමනය පිළිබඳ දැනුම මූලික වශයෙන් වැදගත් වේ, එය නාලිකා ගණන (රේඛා), ස්ථාන සහ නෝඩ් වල උපකරණ පරිමාව තීරණය කරයි. සතියේ එකම දිනයේ ගමනාගමනය සෘතුමය වෙනස්කම් ඇත. සතියේ දිනය පූර්ව නිවාඩු දිනයක් නම්, මෙම දිනයේ NNN නිවාඩු දිනට පසු දිනට වඩා වැඩි වේ. ජාලයෙන් සහය දක්වන සේවා ගණන වැඩි වන විට, තදබදය වැඩි වේ. එබැවින්, රථවාහන කඳු මුදුන් ඇතිවීම ප්‍රමාණවත් විශ්වාසයකින් පුරෝකථනය කිරීම ගැටළු සහගතය. ජාල පරිපාලනය සහ සැලසුම් සංවිධාන විසින් ගමනාගමනය සමීපව නිරීක්ෂණය කරනු ලැබේ. රථවාහන මිනුම් නීති ITU-T විසින් සංවර්ධනය කරන ලද අතර ජාතික ජාල පරිපාලනය විසින් ඔවුන්ගේ ජාලයේ ග්‍රාහකයින් සහ එයට සම්බන්ධ අනෙකුත් ජාල වල ග්‍රාහකයින් සඳහා සේවා අවශ්‍යතාවල ගුණාත්මකභාවය සපුරාලීම සඳහා භාවිතා කරයි. ටෙලිට්‍රාෆික් න්‍යාය අලාභ හෝ ස්ථාන (නෝඩ්) උපකරණ පරිමාව ප්‍රායෝගික ගණනය කිරීම් සඳහා භාවිතා කළ හැක්කේ ගමනාගමනය නිශ්චල (සංඛ්‍යානමය වශයෙන් ස්ථාවර) නම් පමණි. මෙම තත්ත්වය CHNN හි ගමනාගමනය මගින් ආසන්න වශයෙන් තෘප්තිමත් වේ. දිනකට ස්වයංක්‍රීය දුරකථන හුවමාරුව වෙත පැමිණෙන බර ප්‍රමාණය උපකරණ වැළැක්වීම සහ අලුත්වැඩියා කිරීමට බලපායි. දිවා කාලයේදී දුම්රිය ස්ථානයට ඇතුළු වන බරෙහි අසමානතාවය තීරණය වන්නේ සාන්ද්රණ සංගුණකය මගිනි

NNN හි වඩාත් දැඩි නිර්වචනයක් පහත පරිදි සාදා ඇත. ITU නිර්දේශ E.500 ට මාස 12 ක තීව්‍රතා දත්ත විශ්ලේෂණය කිරීම, කාර්යබහුලම දින 30 තේරීම, එම දිනවල කාර්යබහුලම පැය සොයා ගැනීම සහ මෙම කාල පරතරයන් තුළ තීව්‍රතා මිනුම් සාමාන්‍යකරණය කිරීම අවශ්‍ය වේ. මෙම රථවාහන තීව්‍රතාවය (බර) ගණනය කිරීම CHN හෝ A මට්ටමේ රථවාහන තීව්‍රතාවයේ සාමාන්‍ය ඇස්තමේන්තුවක් ලෙස හැඳින්වේ. තෝරාගත් දින 30 කාල සීමාවේ කාර්යබහුලම දින 5 තුළ වඩාත් දැඩි ඇස්තමේන්තුවක් සාමාන්‍යකරණය කළ හැක. මෙම ශ්‍රේණිය වැඩි කළ ශ්‍රේණියක් හෝ B මට්ටමේ ශ්‍රේණියක් ලෙස හැඳින්වේ.

ගමනාගමනය නිර්මාණය කිරීමේ ක්රියාවලිය. දුරකථන ජාලයේ සෑම පරිශීලකයෙකුම දන්නා පරිදි, හඳුන්වන ග්රාහකයා සමඟ සම්බන්ධතාවයක් ඇති කර ගැනීමට සියලු උත්සාහයන් සාර්ථක නොවේ. සමහර විට ඔබ අපේක්ෂිත සම්බන්ධතාවය ස්ථාපිත කිරීමට පෙර අසාර්ථක උත්සාහයන් කිහිපයක් කිරීමට සිදු වේ.

රූපය 10. ග්රාහකයින් අතර සම්බන්ධතාවයක් ස්ථාපනය කිරීමේදී සිදුවීම් රූප සටහන

A සහ B ග්‍රාහකයින් අතර සම්බන්ධතාවයක් ඇති කිරීම අනුකරණය කිරීමේදී සිදුවිය හැකි සිදුවීම් සලකා බලමු (රූපය 10). දුරකථන ජාල වල ඇමතුම් පිළිබඳ සංඛ්‍යාලේඛන පහත පරිදි වේ: සම්පුර්ණ කරන ලද සංවාදවල කොටස 70-50%, අසාර්ථක ඇමතුම්වල කොටස 30-50%. ග්‍රාහකයාගේ ඕනෑම උත්සාහයක් QS ආදානය ලබා ගනී. සාර්ථක උත්සාහයන් සමඟ (සංවාදය සිදු වූ විට), යෙදවුම් සහ ප්‍රතිදානයන් අතර සම්බන්ධතා ඇති කරන ස්විචින් උපාංගවල වාඩිලාගැනීමේ කාලය අසාර්ථක උත්සාහයන්ට වඩා දිගු වේ. ග්‍රාහකයාට ඕනෑම වේලාවක සම්බන්ධතාවයක් ඇති කර ගැනීමේ උත්සාහයට බාධා කළ හැකිය. පහත සඳහන් හේතු නිසා නැවත උත්සාහයන් ඇති විය හැක:

අංකය වැරදි ලෙස අමතන ලදී;

ජාලයේ දෝෂයක් උපකල්පනය කිරීම;

සංවාදයේ හදිසි මට්ටම;

පෙර උත්සාහයන් අසාර්ථක විය;

ග්රාහක B ගේ පුරුදු දැන ගැනීම;

අංකය නිවැරදිව ඇමතීම ගැන සැකයක්.

පහත සඳහන් තත්වයන් මත පදනම්ව නැවත උත්සාහ කළ හැකිය:

හදිසි උපාධි;

අසාර්ථක වීමට හේතු තක්සේරු කිරීම;

නැවත නැවත උත්සාහ කිරීමේ ශක්‍යතාව තක්සේරු කිරීම,

උත්සාහයන් අතර පිළිගත හැකි කාල පරතරය පිළිබඳ ඇස්තමේන්තු.

නැවත උත්සාහ කිරීමට අපොහොසත් වීම අඩු හදිසිතාව නිසා විය හැක. ඇමතුම් මගින් ජනනය වන ගමනාගමන වර්ග කිහිපයක් තිබේ: පැමිණෙන (යෝජිත) Y n සහ මග හැරුණු ගමනාගමනය Y n හි සියලුම සාර්ථක සහ අසාර්ථක උත්සාහයන් ඇතුළත් වේ, Y n හි කොටසක් වන රථවාහන Y n, සාර්ථක සහ සමහර අසාර්ථක උත්සාහයන් ඇතුළත් වේ.

Y pr = Y r + Y np,

මෙහි Y p යනු සංවාදාත්මක (ප්‍රයෝජනවත්) ගමනාගමනය වන අතර Y np යනු අසාර්ථක උත්සාහයන් මගින් ජනනය වන තදබදයයි. Y p = Y p සමානාත්මතාවය ලබා ගත හැක්කේ අලාභයක් නොමැති නම්, ග්‍රාහකයින් ඇමතීමෙන් දෝෂ සහ හැඳින්වෙන ග්‍රාහකයින්ගෙන් ප්‍රතිචාර නොමැති නම් පරමාදර්ශී අවස්ථාවක පමණි.

යම් කාල පරිච්ඡේදයක් තුළ පැමිණෙන සහ සම්ප්රේෂණය කරන ලද බඩු අතර වෙනස නැතිවූ භාරය වනු ඇත.

රථවාහන පුරෝකථනය. සීමිත සම්පත් දුම්රිය ස්ථානය සහ ජාලය ක්‍රමයෙන් ව්‍යාප්ත කිරීමේ අවශ්‍යතාවයට හේතු වේ. ජාල පරිපාලනය සංවර්ධන අදියරේදී ගමනාගමනය වැඩිවීමක් පුරෝකථනය කරයි, එය සැලකිල්ලට ගනිමින්:

ආදායම තීරණය කරනු ලබන්නේ සම්ප්‍රේෂණය වන රථවාහන Y p කොටසෙනි, - පිරිවැය තීරණය වන්නේ ඉහළම තදබදය සහිත සේවාවේ ගුණාත්මකභාවය අනුව ය;

පාඩු විශාල කොටසක් (අඩු ගුණාත්මකභාවය) දුර්ලභ අවස්ථාවන්හිදී සිදු වන අතර එය සංවර්ධන කාල පරිච්ඡේදයේ අවසානය සඳහා සාමාන්ය වේ;

මග හැරුණු ගමනාගමනයේ විශාලතම පරිමාව සිදුවන්නේ ප්‍රායෝගිකව පාඩු නොමැති කාල පරිච්ඡේද තුළ ය - පාඩු 10% ට වඩා අඩු නම්, ග්‍රාහකයින් ඒවාට ප්‍රතිචාර නොදක්වයි. ස්ථාන සහ ජාලය සංවර්ධනය කිරීම සැලසුම් කරන විට, සේවා සැපයීමේ ගුණාත්මකභාවය (පාඩු) සඳහා වන අවශ්යතා මොනවාද යන ප්රශ්නයට නිර්මාණකරු පිළිතුරු දිය යුතුය. මෙය සිදු කිරීම සඳහා, රට තුළ සම්මත කර ඇති නීතිවලට අනුව රථවාහන පාඩු මැනීම අවශ්ය වේ.

රථවාහන මිනුම් උදාහරණය.

පළමුව, යම් ගමනාගමනයට එකවර සේවා සපයන සම්පත් කිහිපයක් ඇති QS හි ක්‍රියාකාරිත්වය ප්‍රදර්ශනය කරන්නේ කෙසේදැයි බලමු. යෙදුම් හෝ අවශ්‍යතා ප්‍රවාහයට සේවය කරන සේවාදායකයන් වැනි සම්පත් ගැන අපි තවදුරටත් කතා කරමු. සේවාදායක සංචිතයක් මගින් ඉල්ලීම් සේවා කිරීමේ ක්‍රියාවලිය නිරූපණය කිරීමට වඩාත්ම දෘශ්‍ය සහ නිතර භාවිතා වන ක්‍රමයක් වන්නේ Gantt chart වේ. මෙම රූප සටහන සෘජුකෝණාස්‍රාකාර ඛණ්ඩාංක පද්ධතියක් වන අතර එය x-අක්ෂයෙන් කාලය නිරූපණය කරන අතර y-අක්ෂය සංචිත සේවාදායකයන්ට අනුරූප වන විවික්ත ලක්ෂ්‍ය සලකුණු කරයි. රූප සටහන 11 මඟින් සේවාදායක තුනක පද්ධතියක් සඳහා Gantt සටහනක් පෙන්වයි.

පළමු කාල අන්තර තුනේදී (අපි ඒවා තත්පරයක් ලෙස සලකමු), පළමු සහ තෙවන සේවාදායකයන් කාර්යබහුලයි, ඊළඟ තත්පර දෙක - තුන්වන පමණි, පසුව දෙවන එක තත්පරයක් සඳහා ක්‍රියා කරයි, පසුව දෙවන සහ පළමු තත්පර දෙක සඳහා , සහ අවසාන තත්පර දෙක - පළමු එක පමණි.

ඉදිකරන ලද රූප සටහන මඟින් ගමනාගමනයේ පරිමාව සහ එහි තීව්‍රතාවය ගණනය කිරීමට ඔබට ඉඩ සලසයි. සේවාදායක මඟින් සේවා කළ නොහැකි ඉල්ලීම් පද්ධතියට ඇතුළු වූයේද යන්න පිළිබඳව කිසිවක් නොකියන බැවින් රූප සටහනෙන් පිළිබිඹු වන්නේ සේවය කළ හෝ මඟ හැරුණු ගමනාගමනය පමණි.

සම්මත වූ ගමනාගමනයේ පරිමාව Gantt ප්‍රස්ථාරයේ සියලුම කොටස්වල මුළු දිග ලෙස ගණනය කෙරේ. තත්පර 10 කින් පරිමාව:

අපි abscissa මත සැලසුම් කර ඇති එක් එක් කාල පරතරය සමඟ සම්බන්ධ කරමු, මෙම ඒකක පරතරය තුළ සිටින සේවාදායකයන් ගණනට සමාන පූර්ණ සංඛ්‍යාවක්. මෙම අගය A(t) යනු ක්ෂණික තීව්‍රතාවයයි. අපගේ උදාහරණය සඳහා

A(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

අපි දැන් තත්පර 10ක කාල සීමාවක් තුළ සාමාන්‍ය ගමනාගමන තීව්‍රතාවය සොයා ගනිමු

මේ අනුව, සලකා බලනු ලබන සේවාදායක තුනක පද්ධතිය විසින් සම්මත කරන ලද ගමනාගමනයේ සාමාන්‍ය තීව්‍රතාවය 1.5 Erl වේ.

මූලික පැටවුම් පරාමිතීන්

දුරකථන සන්නිවේදනය විවිධ කාණ්ඩ ග්‍රාහකයින් විසින් භාවිතා කරනු ලැබේ, ඒවා මගින් සංලක්ෂිත වේ:

පැටවුම් මූලාශ්ර සංඛ්යාව - N,

නිශ්චිත කාලයක් තුළ එක් මූලාශ්‍රයකින් ලැබෙන සාමාන්‍ය ඇමතුම් ගණන (NNN සාමාන්‍යයෙන්) - c,

එක් ඇමතුමක් සේවා කරන විට මාරු කිරීමේ පද්ධතියේ එක් සැසියක සාමාන්ය කාලය t වේ.

බර පැටවීමේ තීව්රතාවය වනු ඇත

විවිධ ඇමතුම් මූලාශ්‍ර හඳුනා ගනිමු. උදාහරණ වශයෙන්,

එක් කාර්යාල දුරකථනයකින් CHN වෙත ලැබෙන සාමාන්‍ය ඇමතුම් සංඛ්‍යාව;

එක් මහල් නිවාස දුරකථනයකින් ලැබෙන ඇමතුම් ගණන; අහඹු සිදුවීම් මහජන සේවා ටෙලි ට්‍රැෆික්

ගණන් කිරීම සමඟ - සාමූහික භාවිතය සඳහා උපකරණයෙන් එකම;

ma සමග - එක් කාසි යන්ත්රයකින් සමාන;

sl සමග - එක් සම්බන්ධක රේඛාවකින් සමාන වේ.

එවිට එක් මූලාශ්‍රයකින් ලැබෙන සාමාන්‍ය ඇමතුම් ගණන:

අනුරූප කාණ්ඩයේ එක් මූලාශ්‍රයකින් ලැබෙන සාමාන්‍ය ඇමතුම් ගණන සඳහා ආසන්න දත්ත තිබේ:

3.5 - 5, =0.5 - 1, ගණන් = 1.5 - 2, ma =15 - 30 සමඟ, sl =10 - 30 සමඟ.

පහත දැක්වෙන ආකාරයේ සම්බන්ධතා ඇත, සම්බන්ධතාවයේ ප්‍රතිඵලය අනුව, දුම්රිය ස්ථානයේ විවිධ දුරකථන පැටවීම් නිර්මාණය කරයි:

k р - සංවාදයෙන් අවසන් වූ සම්බන්ධතා අනුපාතය පෙන්වන සංගුණකය;

k з - ඇමතුම් ග්රාහකයාගේ කාර්යබහුලත්වය හේතුවෙන් සංවාදයෙන් අවසන් නොවූ සම්බන්ධතා;

k නමුත් - කැඳවනු ලබන ග්‍රාහකයාගේ ප්‍රතිචාර නොදැක්වීම හේතුවෙන් සංවාදයෙන් අවසන් නොවූ සම්බන්ධතාවල අනුපාතය ප්‍රකාශ කරන සංගුණකය;

k osh - ඇමතුම්කරුගේ දෝෂ හේතුවෙන් සංවාදයෙන් අවසන් නොවූ සම්බන්ධතා;

k ඒ - තාක්ෂණික හේතූන් මත සංවාදයෙන් අවසන් නොවූ ඇමතුම්.

සාමාන්‍ය ජාල ක්‍රියාකාරිත්වය අතරතුර, මෙම සංගුණකවල අගයන් සමාන වේ:

k p =0.60-0.75; k z =0.12-0.15; k නමුත් =0.08-0.12; k osh =0.02-0.05; k ඒ =0.005-0.01.

සැසියක සාමාන්ය කාලසීමාව සම්බන්ධතා වර්ග මත රඳා පවතී. උදාහරණයක් ලෙස, සම්බන්ධතාවය සංවාදයකින් අවසන් වූවා නම්, උපාංගයේ සාමාන්‍ය කාල සීමාව සමාන වනු ඇත

සම්බන්ධතා ස්ථාපනය කිරීමේ කාලසීමාව කොහිද;

t comp. - සිදු වූ සංවාදයක්;

t in - කැඳවන ලද ග්රාහකයාගේ දුරකථනයට ඇමතුමක් යැවීමේ කාලය;

t r - සංවාදයේ කාලසීමාව

t co යනු දුම්රිය ස්ථාන පිළිතුරු සංඥාව;

1.5n - නම් කරන ලද ග්‍රාහකයාගේ අංකය ඇමතීමට කාලය (n - අංකයේ අක්ෂර ගණන);

t s යනු යාන්ත්‍රණ මාරු කිරීමෙන් සම්බන්ධතාවයක් ඇති කර ගැනීමට සහ සංවාදය අවසන් වූ පසු සම්බන්ධතාවය විසන්ධි කිරීමට අවශ්‍ය කාලයයි. සලකා බලන ලද ප්රමාණවල ආසන්න අගයන්:

t co = 3 තත්පර., t c = 1-2.5 sec., t b = 8-10 sec., t p = 90-130 sec.

සංවාදයෙන් අවසන් නොවන ඇමතුම් ද දුරකථන බරක් ඇති කරයි.

හැඳින්වෙන ග්‍රාහකයා කාර්යබහුල වන විට උපාංගවල රැඳී සිටීමේ සාමාන්‍ය කාලය වේ

t ස්ථාපන සම්බන්ධතාවය කොහෙද (4.2.3) විසින් තීරණය කරනු ලැබේ

t зз - කාර්යබහුල ඝෝෂාව ඇසෙන වේලාව, t зз = 6 තත්.

ඇමතූ ග්‍රාහකයා පිළිතුරු නොදෙන විට උපාංගයේ සාමාන්‍ය කාලසීමාව වේ

එහිදී t pv - රිංග්බැක් සංඥාවට සවන් දෙන වේලාව, t pv = තත්පර 20.

ග්රාහක දෝෂ හේතුවෙන් සංවාදයක් නොතිබුනේ නම්, සාමාන්යයෙන් t osh = 30 තත්පර.

එවැනි පන්තිවල ප්‍රතිශතය කුඩා බැවින් තාක්ෂණික හේතූන් මත සංවාදයෙන් අවසන් නොවූ පන්තිවල කාලසීමාව තීරණය නොවේ.

ඉහත සියල්ලෙන් එය අනුගමනය කරන්නේ CNN පිටුපස ඇති මූලාශ්‍ර සමූහයක් විසින් නිර්මාණය කරන ලද සම්පූර්ණ භාරය එක් එක් ආකාරයේ ක්‍රියාකාරකම්වල බරෙහි එකතුවට සමාන බවයි.

කොටස් වශයෙන් නියමයන් සැලකිල්ලට ගන්නා සංගුණකය කොහෙද

ඉලක්කම් හතක අංක සහිත දුරකථන ජාලයක, ස්වයංක්‍රීය දුරකථන හුවමාරුවක් නිර්මාණය කර ඇති අතර, ග්‍රාහකයින්ගේ ව්‍යුහාත්මක සංයුතිය පහත පරිදි වේ:

N ගිණුම = 4000, N ind = 1000, N ගණන = 2000, N ma = 400, N sl = 400.

CHNN හි එක් මූලාශ්‍රයකින් ලැබෙන සාමාන්‍ය ඇමතුම් ගණන සමාන වේ

සූත්‍ර (4.2.3) සහ (4.2.6) භාවිතා කරමින් අපි භාරය සොයා ගනිමු

1.10.62826767 තත්පර = 785.2 hz.

Y=Nct සූත්‍රයෙන් සාමාන්‍ය පාඩම් කාලය t

t= Y/Nc= 2826767/7800*3.8=95.4 තත්.

කාර්යය පැටවීම

1. ඉලක්කම් හතක් සහිත දුරකථන ජාලයක, ස්වයංක්‍රීය දුරකථන හුවමාරුවක් නිර්මාණය කර ඇති අතර, ග්‍රාහකයින්ගේ ව්‍යුහාත්මක සංයුතිය පහත පරිදි වේ:

N uchr =5000, Nind=1500, N ගණන් =3000, N ma =500, N sl =500.

දුම්රිය ස්ථානයට පැමිණෙන බර තීරණය කරන්න - Y, රැකියාවේ සාමාන්‍ය කාලය t, එය දන්නේ නම්

ind =4 සමඟ, ind =1 සමඟ, ගණන් =2 සමඟ, ma =10 සමග, sl =12 සමඟ, t r =120 තත්., t in =10 sec., k r =0.6, t s =1 තත්., =1.1 .

Allbest.ru හි පළ කර ඇත

සමාන ලියකියවිලි

ඒකාකාරව බෙදා හරින ලද අහඹු විචල්‍යයක සංකල්පය. ගුණ කිරීමේ සමගාමී ක්‍රමය. අඛණ්ඩ අහඹු විචල්‍යයන් සහ විවික්ත ව්‍යාප්ති ආකෘතිකරණය. ණය දෙන්නා සහ ණය ගැණුම්කරු අතර ආර්ථික සබඳතා අනුකරණය කිරීම සඳහා ඇල්ගොරිතම.

පාඨමාලා වැඩ, 01/03/2011 එකතු කරන ලදී


පෝලිම් න්යාය පිළිබඳ පොදු සංකල්ප. ආකෘති පෝලිම් පද්ධතිවල විශේෂාංග. QS පද්ධතිවල රාජ්ය ප්රස්තාර, ඒවා විස්තර කරන සමීකරණ. ආකෘති වර්ගවල පොදු ලක්ෂණ. සුපිරි වෙළඳසැල් පෝලිම් පද්ධතියක් විශ්ලේෂණය.

පාඨමාලා වැඩ, 11/17/2009 එකතු කරන ලදී


පෝලිම් න්‍යායේ මූලද්‍රව්‍ය. පෝලිම් පද්ධතිවල ගණිතමය ආකෘති නිර්මාණය, ඒවායේ වර්ගීකරණය. පෝලිම් පද්ධතිවල සමාකරණ ආකෘති නිර්මාණය. න්‍යායේ ප්‍රායෝගික භාවිතය, ගණිතමය ක්‍රම භාවිතයෙන් ගැටළු විසඳීම.

පාඨමාලා වැඩ, 05/04/2011 එකතු කරන ලදී


අහඹු ක්රියාවලියක සංකල්පය. පෝලිම් න්‍යායේ ගැටළු. පෝලිම් පද්ධති වර්ගීකරණය (QS). සම්භාවිතා ගණිතමය ආකෘතිය. වස්තුවක හැසිරීම මත අහඹු සාධකවල බලපෑම. තනි නාලිකා සහ බහු නාලිකා QS බලා සිටීම.

පාඨමාලා වැඩ, 09/25/2014 එකතු කරන ලදී


පෝලිම් පද්ධතියක්, එහි ප්‍රධාන මූලද්‍රව්‍ය, වර්ගීකරණය, ලක්ෂණ සහ මෙහෙයුම් කාර්යක්ෂමතාවය ඵලදායී ඉදිකිරීම සහ ක්‍රියාත්මක කිරීම පිළිබඳ න්‍යායික අංශ අධ්‍යයනය කිරීම. GPSS භාෂාව භාවිතයෙන් පෝලිම් පද්ධතියක් ආදර්ශණය කිරීම.

පාඨමාලා වැඩ, 09/24/2010 එකතු කරන ලදී


ගතික වැඩසටහන්කරණය, ජාල සැලසුම්කරණය සහ නිෂ්පාදන නිෂ්පාදන කළමනාකරණය පිළිබඳ න්‍යාය වර්ධනය කිරීම. ආර්ථික ක්‍රියාවලීන් ආකෘතිකරණය කිරීමේ ගැටළු වල ක්‍රීඩා න්‍යායේ සංරචක. පෝලිම් න්‍යායේ ප්‍රායෝගික යෙදුමේ මූලිකාංග.

ප්‍රායෝගික වැඩ, 01/08/2011 එකතු කරන ලදී


අහඹු සිදුවීම්, ප්‍රමාණ සහ කාර්යයන් පිළිබඳ මූලික සංකල්ප. අහඹු විචල්‍යවල සංඛ්‍යාත්මක ලක්ෂණ. බෙදා හැරීමේ අසමමිතිය වර්ග. අහඹු විචල්‍ය ව්‍යාප්තිය පිළිබඳ සංඛ්‍යානමය තක්සේරුව. ව්යුහාත්මක-පරාමිතික හඳුනාගැනීමේ ගැටළු විසඳීම.

පාඨමාලා වැඩ, 03/06/2012 එකතු කරන ලදී


පෝලිම් ක්රියාවලිය ආදර්ශනය කිරීම. විවිධ වර්ගයේ පෝලිම් නාලිකා. අසාර්ථකත්වයන් සහිත තනි නාලිකා පෝලිම් ආකෘතියක විසඳුම. සේවා කාලය බෙදා හැරීමේ ඝනත්වය. නිරපේක්ෂ ප්‍රතිදානය තීරණය කිරීම.

පරීක්ෂණය, 03/15/2016 එකතු කරන ලදී


මාර්ග ප්‍රවාහන ක්ෂේත්‍රයේ පෝලිම් පද්ධතියේ ක්‍රියාකාරී ලක්ෂණ, එහි ව්‍යුහය සහ ප්‍රධාන අංග. පෝලිම් පද්ධතියේ ක්රියාකාරිත්වයේ ගුණාත්මකභාවය පිළිබඳ ප්රමාණාත්මක දර්ශක, ඔවුන්ගේ නිර්ණය කිරීමේ අනුපිළිවෙල සහ ප්රධාන අදියර.

රසායනාගාර කටයුතු, 03/11/2011 එකතු කරන ලදී


ආකෘති නිර්මාණය කිරීමේ ඉලක්කය සැකසීම. සැබෑ වස්තූන් හඳුනා ගැනීම. ආකෘති වර්ගය තෝරාගැනීම, ගණිතමය යෝජනා ක්රමය. අඛණ්ඩ-ස්ථිතික ආකෘතියක් ඉදිකිරීම. පෝලිම් න්‍යායේ මූලික සංකල්ප. සිදුවීම් ගලායාම නිර්වචනය කරන්න. ඇල්ගොරිතම සැකසීම.