Що має трикутник? Як називаються кути трикутника. Співвідношення у трикутнику

Якщо три точки, що не лежать на одній прямій, з'єднати відрізками, отримаємо трикутник. Одну зі сторін трикутника часто називають його основою.

Теорема.Сума кутів трикутника дорівнює 180 0

Якщо всі три кути трикутника гострі, то трикутник називається гострокутним.

Якщо один із кутів трикутника тупий, то трикутник називається тупокутним.

Якщо один із кутів трикутника прямий, то трикутник називається прямокутним. Сторона прямокутного трикутника, що лежить проти прямого кута, називається гіпотенузою, а дві інші сторони - катетами.

У будь-якому трикутнику проти більшої сторони лежить більший кут; проти рівних сторін - рівні кути, і назад. Будь-яка сторона трикутника менша від суми двох інших сторін, а також більше різниці двох інших сторін.

Продовживши одну із сторін трикутника, отримаємо зовнішній кут. Кут АВD - зовнішній.

Ознаки рівності трикутників

Якщо два трикутники рівні, то елементи (сторони та кути) одного трикутника відповідно дорівнюють елементам іншого трикутника.

Теорема.Два трикутники рівні, якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого.

Теорема.Два трикутники рівні, якщо сторона і два кути одного трикутника, що прилягають до неї, рівні відповідно до сторони і двох прилеглих кутів іншого.

Теорема.Два трикутники рівні, якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого.

Медіана, бісектриса та висота трикутника

Відрізок, що з'єднує вершину трикутника із серединою протилежної сторони, називається медіаноютрикутник.

Промінь, що виходить з вершини кута і ділить його на два рівні кути, називається бісектрисою. Бісектриса ділить протилежну сторону на частини, пропорційні сторонам, що прилягають до неї.

Перпендикуляр, проведений з вершини трикутника до прямої, що містить протилежну сторону, називається заввишкитрикутник.

Чудові точки трикутника. 1) Бісектриси трикутника перетинаються в одній точці.

2) Серединні перпендикуляри до сторін трикутника перетинаються в одній точці.

3) Висоти трикутника (або їх продовження) перетинаються в одній точці.

4) Медіани трикутника перетинаються в одній точці.

Рівнобедрений трикутник

Трикутник називається рівнобедреним, якщо дві його сторони рівні. Рівні сторони називаються бічними сторонами, а третя сторона - основоюрівнобедреного трикутника.

Трикутник, у якого усі сторони рівні, називається рівностороннім.

Теорема.У рівнобедреному трикутнику кути при основі рівні.

Теорема.У рівнобедреному трикутнику бісектриса, проведена до основи, є медіаною та висотою.

Що таке трикутник, квадрат, куб, нам розповідає наука геометрія. У світі її вивчають у школах все без винятку. Також наукою, яка вивчає те, що таке трикутник і які у нього властивості, є тригонометрія. Вона досліджує докладно всі явища, пов'язані з даними Про те, що таке трикутник, ми поговоримо сьогодні в нашій статті. Нижче буде описано їх види, а також деякі теореми, пов'язані з ними.

Що таке трикутник? Визначення

Це плаский багатокутник. Кутів він має три, що зрозуміло з його назви. Також він має три сторони і три вершини, перші з них це відрізки, другі точки. Знаючи, чому рівні два кути, можна знайти третій, відібравши суму перших двох від числа 180.

Якими є трикутники?

Їх можна класифікувати за різними критеріями.

Насамперед вони діляться на гострокутні, тупокутні та прямокутні. Перші мають гострі кути, тобто такі, які рівні менш ніж 90 градусів. У тупокутних один із кутів — тупий, тобто такий, що дорівнює понад 90 градусів, решта — гострі. До гострокутних трикутників відносяться також рівносторонні. У таких трикутників усі сторони та кути рівні. Всі вони дорівнюють 60 градусам, це можна легко обчислити, розділивши суму всіх кутів (180) на три.

Прямокутний трикутник

Неможливо не поговорити, що таке прямокутний трикутник.

У такої фігури один кут дорівнює 90 градусів (прямий), тобто дві його сторони розташовані перпендикулярно. Інші два кути є гострими. Вони можуть бути рівними, тоді він буде рівнобедреним. З прямокутним трикутником пов'язана теорема Піфагора. За її допомогою можна знайти третю сторону, знаючи дві перші. Згідно з цією теоремою, якщо додати квадрат одного катета до квадрата іншого, можна отримати квадрат гіпотенузи. Квадрат катета можна підрахувати, відібравши від квадрата гіпотенузи квадрат відомого катета. Говорячи про те, що таке трикутник, можна згадати і рівнобедрений. Це такий, у якого дві зі сторін рівні, також рівні і два кути.

Що таке катет та гіпотенуза?

Катет - це одна зі сторін трикутника, які утворюють кут 90 градусів. Гіпотенуза - це сторона, що залишилася, яка розташована навпроти прямого кута. З нього на катет можна опустити перпендикуляр. Ставлення прилеглого катета до гіпотенузи називається не інакше як косинус, а протилежного синус.

- У чому його особливості?

Він прямокутний. Його катети дорівнюють трьом і чотирьом, а гіпотенуза — п'яти. Якщо ви побачили, що катети даного трикутника рівні трьох і чотирьох, можете не сумніватися, що гіпотенуза дорівнюватиме п'яти. Також за таким принципом можна легко визначити, що катет дорівнюватиме трьом, якщо другий дорівнює чотирьом, а гіпотенуза - п'яти. Щоб довести твердження, можна застосувати теорему Піфагора. Якщо два катети дорівнюють 3 і 4, то 9 + 16 = 25, корінь з 25 - це 5, тобто гіпотенуза дорівнює 5. Також єгипетським трикутником називається прямокутний, сторони якого дорівнюють 6, 8 і 10; 9, 12 та 15 та іншим числам із співвідношенням 3:4:5.

Яким ще може бути трикутник?

Також трикутники можуть бути вписаними та описаними. Фігура, навколо якої описана коло, називається вписаною, всі її вершини є точками, що лежать на колі. Описаний трикутник - той, в який вписано коло. Усі його сторони стикаються з нею у певних точках.

Як знаходиться

Площа будь-якої фігури вимірюється в квадратних одиницях (кв. метрах, кв. міліметрах, кв. сантиметрах, кв. дециметрах і т. д.). Дану величину можна розрахувати різноманітними способами, залежно від виду трикутника. Площа будь-якої фігури з кутами можна знайти, якщо помножити її сторону на перпендикуляр, опущений на неї з протилежного кута, і розділивши цю цифру на два. Також можна знайти цю величину, якщо помножити дві сторони. Потім помножити це число на синус кута, розташованого між цими сторонами, і розділити це, що вийшло на два. Знаючи всі сторони трикутника, але не знаючи його кутів, можна знайти площу ще й іншим способом. Для цього необхідно знайти половину периметра. Потім по черзі відібрати від цього числа різні сторони і перемножити отримані чотири значення. Далі знайти з числа, що вийшло. Площа вписаного трикутника можна знайти, перемноживши всі сторони і розділивши отримане число, на яку описано навколо нього, помножений на чотири.

Площа описаного трикутника знаходиться таким чином: половину периметра множимо на радіус кола, яке в нього вписано. Якщо його площа можна знайти таким чином: сторону зводимо в квадрат, множимо отриману цифру на корінь з трьох, далі ділимо це число на чотири. Подібним чином можна вирахувати висоту трикутника, у якого всі сторони рівні, для цього одну з них потрібно помножити на корінь з трьох, а потім розділити це число на два.

Теореми, пов'язані з трикутником

Основними теоремами, пов'язані з цією фігурою, є теорема Піфагора, описана вище, і косінусів. Друга (синусів) полягає в тому, що якщо розділити будь-яку сторону на синус протилежного їй кута, то можна отримати радіус кола, яке описано навколо нього, помножений на два. Третя (косінусів) полягає в тому, що, якщо від суми квадратів двох сторін відібрати їх же твір, помножений на два і на косинус кута, розташованого між ними, то вийде квадрат третьої сторони.

Трикутник Далі - що це?

Багато хто, зіткнувшись із цим поняттям, спочатку думає, що це якесь визначення в геометрії, але це зовсім не так. Трикутник Далі - це загальна назва трьох місць, які тісно пов'язані із життям знаменитого художника. «Вершинами» його є будинок, в якому жив Сальвадор Далі, замок, який він подарував своїй дружині, а також музей сюрреалістичних картин. Під час екскурсії цими місцями можна дізнатися багато цікавих фактів про цього своєрідного креативного художника, відомого у всьому світі.

Стандартні позначення

Трикутник з вершинами A, Bі Cпозначається як (див. мал.). Трикутник має три сторони:

Довжини сторін трикутника позначаються малими латинськими літерами (a, b, c):

Трикутник має такі кути:

Величини кутів за відповідних вершин традиційно позначаються грецькими літерами (α, β, γ).

Ознаки рівності трикутників

Трикутник на евклідовій площині однозначно (з точністю до конгруентності) можна визначити за такими трійками основних елементів:

1. a, b, γ (рівність з двох сторін і куту, що лежить між ними);
2. a, β, γ (рівність по стороні та двом прилеглим кутам);
3. a, b, c (рівність по трьох сторонах).

Ознаки рівності прямокутних трикутників:

1. з катету та гіпотенузи;
2. за двома катетами;
3. по катету та гострому кутку;
4. з гіпотенузи та гострого кута.

Деякі точки у трикутнику – «парні». Наприклад, існує дві точки, з яких всі сторони видно або під кутом 60°, або під кутом 120°. Вони називаються точками Торрічеллі. Існує також дві точки, проекції яких на сторони лежать у вершинах правильного трикутника. Це - точки Аполлонія. Крапки і такі, що називаються точками Брокара.

Прямі

У будь-якому трикутнику центр тяжіння, ортоцентр і центр описаного кола лежать на одному прямому, званому прямий Ейлера.

Пряма, що проходить через центр описаного кола та точку Лемуана, називається віссю Брокара. На ній лежать точки Аполлонія. Також на одній прямій лежать точки Торрічеллі та точка Лемуана. Основи зовнішніх бісектрис кутів трикутника лежать на одній прямій, званій віссю зовнішніх бісектрис. На одній прямій також лежать точки перетину прямих, що містять сторони ортотрикутника, з прямими, що містять сторони трикутника. Ця пряма називається ортоцентричною віссю, вона перпендикулярна до прямої Ейлера.

Якщо на описаному колі трикутника взяти крапку, то її проекції на сторони трикутника лежатимуть на одній прямій, званій прямий Сімсонацієї точки. Прямі Сімсона діаметрально протилежних точок перпендикулярні.

Трикутники

• Трикутник з вершинами в підставах чевіан, проведених через цю точку, називається чевіанним трикутникомцієї точки.
• Трикутник з вершинами в проекціях цієї точки на сторони називається подернимабо педальним трикутникомцієї точки.
• Трикутник у вершинах у других точках перетину прямих, проведених через вершини і дану точку, з описаним колом, називають окружно-чевіанним трикутником. Окружно-чевіанний трикутник подібний до подерного.

Кола

• Вписане коло- Коло , Що стосується всіх трьох сторін трикутника. Вона єдина. Центр вписаного кола називається інцентром.
• Описане коло- Коло, що проходить через всі три вершини трикутника. Описане коло також єдине.
• Не вписане коло- коло, що стосується однієї сторони трикутника та продовження двох інших сторін. Таких кіл у трикутнику три. Їхній радикальний центр - центр вписаного кола серединного трикутника, званий точкою Шпікера.

Середини трьох сторін трикутника, основи трьох його висот і середини трьох відрізків, що з'єднують його вершини з ортоцентром, лежать на одному колі, що називається коло дев'яти точокабо коло Ейлера. Центр кола дев'яти точок лежить на прямій Ейлера. Окружність дев'яти точок стосується вписаного кола і трьох вписаних. Крапка торкання вписаного кола та кола дев'яти точок називається точкою Фейєрбаха. Якщо від кожної вершини відкласти назовні трикутника на прямих, що містять сторони, ортезки, рівні по довжині протилежним сторонам, то шість точок, що виходять, лежать на одному колі - кола Конвею. У будь-який трикутник можна вписати три кола таким чином, що кожна з них стосується двох сторін трикутника та двох інших кіл. Такі кола називаються коло Мальфатті. Центри описаних кіл шести трикутників, на які трикутник розбивається медіанами, лежать на одному колі, яке називається коло Ламуна.

У трикутнику є три кола, які стосуються двох сторін трикутника та описаного кола. Такі кола називають напіввписанимиабо коло Верр'єра. Відрізки, що з'єднують точки дотику кіл Верр'єра з описаним колом, перетинаються в одній точці, званій точкою Верр'єра. Вона служить центром гомотетії, яка переводить описане коло у вписане. Точки торкання кіл Верр'єра зі сторонами лежать на прямій, яка проходить через центр вписаного кола.

Відрізки, що з'єднують точки торкання вписаного кола з вершинами, перетинаються в одній точці, що називається точкою Жергона, а відрізки, що з'єднують вершини з точками дотику до вписаних кіл - в точці Нагеля.

Еліпси, параболи та гіперболи

Вписана коніка (еліпс) та її перспектор

У трикутник можна вписати нескінченно багато кузнечиків (еліпсів, парабол або гіпербол). Якщо в трикутник вписати довільну коніку і з'єднати точки торкання з протилежними вершинами, то прямі, що вийшли, перетнуться в одній точці, званій перспективоюконики. Для будь-якої точки площини, що не лежить на боці або її продовженні існує вписана коніка з перспективою в цій точці.

Описаний еліпс Штейнера та чевіани, що проходять через його фокуси

У трикутник можна вписати еліпс, що стосується сторін у серединах. Такий еліпс називається вписаним еліпсом Штейнера(його перспективою буде центроїд трикутника). Описаний еліпс, що стосується прямих, що проходять через вершини паралельно сторонам, називається описаним еліпсом Штейнера. Якщо афінним перетворенням («перекосом») перевести трикутник у правильний, його вписаний і описаний еліпс Штейнера перейдуть у вписану і описану окружності. Чевіани, проведені через фокуси описаного еліпса Штейнер (точки Скутіна), рівні (теорема Скутіна). З усіх описаних еліпсів описаний еліпс Штейнера має найменшу площу, а з усіх вписаних найбільшу площу має вписаний еліпс Штейнера.

Елліпс Брокара та його перспектор - точка Лемуана

Еліпс з фокусами у точках Брокара називається еліпсом Брокара. Його перспективою служить точка Лемуана.

Властивості вписаної параболи

Парабола Кіперта

Перспектори вписаних параболів лежать на описаному еліпсі Штейнера. Фокус вписаної параболи лежить на описаному колі, а директриса проходить через ортоцентр. Парабола, вписана в трикутник, що має директрису пряму Ейлера, називається параболою Кіперта. Її перспектор - четверта точка перетину описаного кола та описаного еліпса Штейнера, звана точкою Штейнера.

Гіпербола Кіперта

Якщо описана гіпербола проходить через точку перетину висот, вона рівностороння (тобто її асимптоти перпендикулярні). Точка перетину асимптот рівносторонньої гіперболи лежить на колі дев'яти точок.

Перетворення

Якщо прямі, що проходять через вершини та деяку точку, що не лежить на сторонах та їх продовженнях, відобразити щодо відповідних бісектрис, то їх образи також перетнуться в одній точці, яка називається ізогонально пов'язаноївихідної (якщо точка лежала на описаному колі, то прямі будуть паралельні). Ізгонально пов'язаними є багато пар чудових точок: центр описаного кола і ортоцентр, центроїд і точка Лемуана, точки Брокара. Крапки Аполлонія вигнано пов'язані точкам Торрічеллі, а центр вписаного кола вигнано пов'язаний сам собі. Під дією ізогонального сполучення прямі переходять у описані кузнечики, а описані кузнечики - у прямі. Так, ізогонально пов'язані гіпербола Кіперта та вісь Брокара, гіпербола Енжабека та пряма Ейлера, гіпербола Фейєрбаха та лінія центрів вписаної про описані кола. Описані кола подерних трикутників ізгонально сполучених точок збігаються. Фокуси вписаних еліпсів ізгонально пов'язані.

Якщо замість симетричної чевіани брати чевіану, основа якої віддалена від середини сторони так само, як і основа вихідної, такі чевіани також перетнуться в одній точці. Перетворення, що вийшло, називається ізотомічним поєднанням. Воно також переводить прямі в описані коніки. Ізотомічно пов'язані точки Жергона та Нагеля. При афінних перетвореннях ізотомічно сполучені точки переходять в ізотомічно сполучені. При ізотомічному поєднанні в нескінченно віддалену пряму перейде описаний еліпс Штейнера.

Якщо сегменти, що відсікаються сторонами трикутника від описаного кола, вписати кола, що стосуються сторін в підставах чевіан, проведених через деяку точку, а потім з'єднати точки торкання цих кіл з описаним колом з протилежними вершинами, то такі прямі перетинаються в одній точці. Перетворення площини, що співставляє вихідній точці, називається ізоциркулярним перетворенням. Композиція ізогонального та ізотомічного сполучення є композицією ізоциркулярного перетворення з самим собою. Ця композиція - проективне перетворення, яке сторони трикутника залишає на місці, а вісь зовнішніх бісектрис переводить у нескінченно віддалену пряму.

Якщо продовжити сторони чевіанного трикутника деякої точки та взяти їх точки перетину з відповідними сторонами, то отримані точки перетину лежатимуть на одній прямій, званій трилінійною поляроювихідної точки. Ортоцентрична вісь – трилінійна поляра ортоцентру; Трилінійною полярою центру вписаного кола служить вісь зовнішніх бісектрис. Трилінійні поляри точок, що лежать на описаній коніці, перетинаються в одній точці (для описаного кола це точка Лемуана, для описаного еліпса Штейнера – центроїд). Композиція ізогонального (або ізотомічного) сполучення і трилінійної поляри є перетворенням двоїстості (якщо точка, ізогонально (ізотомічно) сполучена точці , лежить на трилінійній полярі точки , то трилінійна поляра точки, ізогонально (ізотомічно) спряженої точки).

Кубики

Співвідношення у трикутнику

Примітка:в даному розділі , , - це довжини трьох сторін трикутника, і , , - це кути, що лежать відповідно напроти цих трьох сторін (протилежні кути).

Нерівність трикутника

У невиродженому трикутнику сума довжин двох його сторін більша за довжину третьої сторони, у виродженому - дорівнює. Інакше висловлюючись, довжини сторін трикутника пов'язані наступними нерівностями:

Нерівність трикутника є однією з аксіом метрики.

Теорема про суму кутів трикутника

Теорема синусів

де R - радіус кола, описаного навколо трикутника. З теореми випливає, що якщо a< b < c, то α < β < γ.

Теорема косінусів

Теорема тангенсів

Інші співвідношення

Метричні співвідношення в трикутнику наведені для:

Рішення трикутників

Обчислення невідомих сторін та кутів трикутника, виходячи з відомих, історично одержало назву «рішення трикутників». При цьому використовуються наведені вище загальні тригонометричні теореми.

Площа трикутника

Для площі справедливі нерівності:

Обчислення площі трикутника у просторі за допомогою векторів

Нехай вершини трикутника перебувають у точках , , .

Введемо вектор площі. Довжина цього вектора дорівнює площі трикутника, а спрямований по нормалі до площини трикутника:

Покладемо , де , - проекції трикутника на координатні площини. При цьому

та аналогічно

Площа трикутника дорівнює.

Альтернативою служить обчислення довжин сторін (за теоремою Піфагора) і далі за формулою Герона.

Теореми про трикутники

Трикутник . Гострокутний, тупокутний та прямокутний трикутник.

Катети та гіпотенуза. Рівностегновий та рівносторонній трикутник.

Сума кутів трикутника.

Зовнішній кут трикутника. Ознаки рівності трикутників.

Чудові лінії та точки у трикутнику: висоти, медіани,

бісектриси, середні e перпендикуляри, ортоцентр,

центр тяжкості, центр кола, центр вписаного кола.

Теорема Піфагора. Співвідношення сторін у довільному трикутнику.

Трикутник – це багатокутник із трьома сторонами (або трьома кутами). Сторони трикутника позначаються часто малими літерами, які відповідають великим літерам, що позначають протилежні вершини.

Якщо всі три кути гострі (рис.20), то це гострокутний трикутник . Якщо один із кутів прямий(C, рис.21), то це прямокутний трикутник; сторониa, b, що утворюють прямий кут, називаються катетами; сторонаc, протилежна прямому куту, називається гіпотенузою. Якщо один ізкутів тупий (B, рис.22), то це тупокутний трикутник.


Трикутник ABC (рис.23) - рівнобедрений, якщо двійого сторони рівні (a= c); ці рівні сторони називаються бічними, третя сторона називається основоютрикутник. Трикутник ABC (рис.24) - рівносторонній, якщо Усейого сторони рівні (a = b = c). У загальному випадку ( a ≠ b ≠ c) маємо нерівностороннійтрикутник .

Основні властивості трикутників. У будь-якому трикутнику:

1. Проти більшої сторони лежить більший кут, і навпаки.

2. Проти рівних сторін лежать рівні кути, і навпаки.

Зокрема, всі кути в рівностороннійтрикутнику рівні.

3. Сума кутів трикутника дорівнює 180 º .

З двох останніх властивостей випливає, що кожен кут у рівносторонньому

трикутнику дорівнює 60 º.

4. Продовжуючи одну із сторін трикутника (AC, рис.25), отримуємо зовнішній

кут BCD . Зовнішній кут трикутника дорівнює сумі внутрішніх кутів,

не суміжних з ним : BCD = A + B.

5. Будь-яка сторона трикутника менша від суми двох інших сторін і більша

їх різниці (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Ознаки рівності трикутників.

Трикутники рівні, якщо вони відповідно рівні:

a ) дві сторони та кут між ними;

b ) два кути і прилегла до них сторона;

c) три сторони.

Ознаки рівності прямокутних трикутників.

Два прямокутнихтрикутника рівні, якщо виконується одна з наступних умов:

1) рівні їх катети;

2) катет та гіпотенуза одного трикутника рівні катету та гіпотенузі іншого;

3) гіпотенуза та гострий кут одного трикутника рівні гіпотенузі та гострому куту іншого;

4) катет і прилеглий гострий кут одного трикутника рівні катету та прилеглого гострого кута іншого;

5) катет і протилежний гострий кут одного трикутника дорівнюють катету і протилежному гострому кутку іншого.

Чудові лінії та точки у трикутнику.

Висота трикутника - цеперпендикуляр,опущений з будь-якої вершини на протилежний бік ( або її продовження). Ця сторона називаєтьсяосновою трикутника . Три висоти трикутника завжди перетинаютьсяв одній точцізваної ортоцентромтрикутник. Ортоцентр гострокутного трикутника (точка O , рис.26) розташований усередині трикутника, аортоцентр тупокутного трикутника (точка O , мал.27) – зовні; Ортоцентр прямокутного трикутника збігається з вершиною прямого кута.

Медіана – це відрізок , що з'єднує будь-яку вершину трикутника із серединою протилежної сторони. Три медіани трикутника (AD, BE, CF, мал.28) перетинаються в одній точці O завжди лежить всередині трикутникаі є його центром важкості. Ця точка ділить кожну медіану щодо 2:1, рахуючи від вершини.

Бісектриса – це відрізок бісектрисикута від вершини до точки перетину з протилежною стороною. Три бісектриси трикутника (AD, BE, CF, мал.29) перетинаються в одній точці О, що завжди лежить усередині трикутникаі що є центром вписаного кола(див. розділ «Вписаніта описані багатокутники»).

Бісектриса ділить протилежний бік на частини, пропорційні прилеглим сторонам ; наприклад, на рис.29 AE: CE = AB: BC.

Серединний перпендикуляр – це перпендикуляр, проведений із середньоїточки відрізка (сторони). Три серединні перпендикуляри трикутника АВС(KO, MO, NO, рис.30 ) перетинаються в одній точці О, що є центром описаного кола (точки K, M, N – середини сторін трикутника ABC).

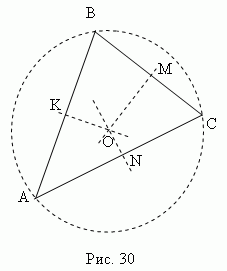
У гострокутному трикутнику ця точка лежить усередині трикутника; у тупокутному – зовні; у прямокутному - у середині гіпотенузи. Ортоцентр, центр тяжкості, центр описаного та центр вписаного кола збігаються лише у рівносторонньому трикутнику.

Теорема Піфагора. У прямокутному трикутнику квадрат довжинигіпотенузи дорівнює сумі квадратів довжин катетів.

Доказ теореми Піфагора очевидно випливає з рис.31. Розглянемо прямокутний трикутник ABC з катетами a, bта гіпотенузою c.

Побудуємо квадрат AKMB , використовуючи гіпотенузу AB як бік. Потімпродовжимо сторони прямокутного трикутника ABC так, щоб отримати квадрат CDEF , сторона якого дорівнюєa + b.Тепер ясно, що площа квадрата CDEF дорівнює ( a + b) 2 . З іншого боку, ця площа дорівнює суміплощ чотирьох прямокутних трикутниківі квадрата AKMB, тобто

c 2 + 4 (ab / 2) = c 2 + 2 ab

звідси,

c 2 + 2 ab= (a + b) 2 ,

і остаточно маємо:

c 2 =a 2 + b 2 .

Співвідношення сторін у довільному трикутнику.

У загальному випадку (для довільного трикутника) маємо:

c 2 =a 2 + b 2 – 2ab· cos C,

де C – кут між сторонамиaі b .

Як називаються кути трикутника? Відповідь може залежати від того, скільки кутів є на вершині трикутника.

Якщо при трикутнику є тільки один кут, його можна назвати однією літерою, за назвою вершини.

Наприклад, у трикутнику MKF (малюнок 1) при кожній вершині є лише один кут. Отже, кожен з кутів можна назвати однією літерою, за назвою вершини, з якої виходять промені, що утворюють цей кут:

малюнок 1

Кут M, кут K та кут F.

Для позначення кута існує спеціальний знак: ∠

Запис ∠M читають як «кут M».

Кожен із кутів трикутника MKF можна назвати також трьома літерами. При цьому вершина у назві кута має стояти посередині.

Кут M також можна назвати кутом KMF або кутом FMK,

∠K - ∠MKF або ∠FKM,

∠F - ∠MFK або ∠KFM.

малюнок 2

У трикутниках, зображених на малюнку 2, однією літерою можуть бути названі лише кути при вершинах A та D: ∠A та ∠D.

При вершині B є три кути, тому кожен із цих кутів потрібно назвати трьома літерами: ∠ABC, ∠CBD та ∠ABD.

Аналогічно, кути при вершині C можуть бути названі лише трьома літерами: ∠ACB, ∠BCD та ∠ACD. Назвати якийсь із цих кутів ∠C не можна.

малюнок 3

Кожен із кутів трикутників, зображених на малюнку 3, може бути названий лише трьома літерами.

Кути трикутника ABO: ∠ABO, ∠BAO, ∠AOB.

Кути трикутника BOC: ∠BOC, ∠OBC, ∠BCO.

Кути трикутника OCD: ∠OCD, ∠COD, ∠CDO.

Кути трикутника AOD: ∠AOD, ∠ADO,∠OAD.

Кути трикутника ABC: ∠ABC, ∠BAC, ∠BCA.

Кути трикутника BCD: ∠BCD, ∠CBD, ∠BDC.

Кути трикутника ACD: ∠ACD, ∠CAD, ∠ADC.

Кути трикутника ABD: ∠ABD, ∠BAD, ∠ADB.