Вертикальні асимптоти до графіка функції мають вигляд. Асимптоти графіка функції. Скільки асимптот може бути у графіка функції
Асимптоти графіка функції
Привид асимптоти давно бродив по сайту щоб, нарешті, матеріалізуватися в окремо взятій статті і привести в особливий захват читачів, спантеличених повним дослідженням функції. Знаходження асимптот графіка - одна з небагатьох частин зазначеного завдання, яка висвітлюється в шкільному курсі лише в оглядовому порядку, оскільки події обертаються навколо обчислення меж функцій, А вони відносяться все-таки до вищої математики. Відвідувачі, слабо розбираються в математичному аналізі, натяк, думаю, зрозумілий ;-) ... стоп-стоп, ви куди? межі - це легко!
Приклади асимптот зустрілися відразу ж на першому уроці про графіках елементарних функцій, І зараз тема отримує детальний розгляд.
Отже, що таке асимптота?
Уявіть змінну точку, Яка «їздить» по графіку функції. Асимптота - це пряма, До якої необмежено близько наближається графік функції при видаленні його змінної точки в нескінченність.
Примітка : Визначення змістовно, якщо вам необхідна формулювання в позначеннях математичного аналізу, будь ласка, зверніться до підручника.
На площині асимптоти класифікують за їх природному розташуванню:
1) вертикальні асимптоти, Які задаються рівнянням виду, де «альфа» - дійсне число. Популярна представниця визначає саму вісь ординат,
з нападом легкої нудоти згадуємо гіперболу.
2) похилі асимптоти традиційно записуються рівнянням прямої з кутовим коефіцієнтом. Іноді окремою групою виділяють окремий випадок - горизонтальні асимптоти. Наприклад, та ж гіпербола з асимптотой.
Жваво пішло-поїхало, вдаримо по темі короткою автоматною чергою:
Скільки асимптот може бути у графіка функції?
Жодної, одна, дві, три, ... або нескінченно багато. За прикладами далеко ходити не будемо, згадаємо елементарні функції. Парабола, кубічна парабола, синусоїда зовсім не мають асимптот. Графік експоненційної, логарифмічної функції володіє єдиною асимптотой. У арктангенса, арккотангенса їх дві, а у тангенса, котангенса - нескінченно багато. Не рідкість, коли графік укомплектований і горизонтальними і вертикальними асимптотами. Гіпербола, will always love you.
Що значить ?
Вертикальні асимптоти графіка функції
Вертикальна асимптота графіка, як правило, знаходиться в точці нескінченного розриву функції. Все просто: якщо в точці функція терпить нескінченний розрив, то пряма, задана рівнянням є вертикальною асимптотой графіка.
Примітка : Зверніть увагу, що запис використовується для позначення двох абсолютно різних понять. Точка мається на увазі або рівняння прямої - залежить від контексту.
Таким чином, щоб встановити наявність вертикальної асимптоти в точці досить показати, що хоча б один з односторонніх меж 
нескінченний. Найчастіше це точка, де знаменник функції дорівнює нулю. По суті, ми вже знаходили вертикальні асимптоти в останніх прикладах уроку про безперервність функції. Але в ряді випадків існує тільки один односторонній межа, і, якщо він нескінченний, то знову - любите і жалуйте вертикальну асимптоту. Найпростіша ілюстрація: і вісь ординат (див. Графіки і властивості елементарних функцій).
З вищесказаного також випливає очевидний факт: якщо функція неперервна на, То вертикальні асимптоти відсутні. На думку чомусь прийшла парабола. Дійсно, де тут «воткнёшь» пряму? ... да ... розумію ... послідовники дядечка Фрейда забилися в істериці \u003d)
Протилежне твердження в загальному випадку невірно: так, функція не визначена на всій числовій прямій, проте абсолютно обділена асимптотами.
Похилі асимптоти графіка функції
Похилі (як окремий випадок - горизонтальні) асимптоти можуть намалюватися, якщо аргумент функції прагне до «плюс нескінченності» або до «мінус нескінченності». Тому графік функції не може мати більше двох похилих асимптот. Наприклад, графік експоненціальної функції володіє єдиною горизонтальною асимптотой при, а графік арктангенса при - двома такими асимптотами, причому різними.
Коли графік і там і там зближується з єдиною похилій асимптотой, то «нескінченності» прийнято об'єднувати під єдиною записом. Наприклад, ... правильно здогадалися:.
Загальна практичне правило:
Якщо існують два кінцевих межі 
, То пряма є похилою асимптотой графіка функції при. якщо хоча б один з перерахованих меж нескінченний, то похила асимптота відсутня.
Примітка : Формули залишаються справедливими, якщо «ікс» прагне тільки до «плюс нескінченності» або тільки до «мінус нескінченності».
Покажемо, що у параболи немає похилих асимптот: 
Межа нескінченний, значить, похила асимптота відсутня. Зауважте, що в знаходженні межі 
необхідність відпала, оскільки відповідь вже отримано.
Примітка
: Якщо у вас виникли (або виникнуть) труднощі з розумінням знаків «плюс-мінус», «мінус-плюс», будь ласка, подивіться довідку на початку уроку
про нескінченно малих функціях, Де я розповів, як правильно інтерпретувати дані знаки.
Очевидно, що у будь-який квадратичної, кубічної функції, многочлена 4-й і вищих ступенів також немає похилих асимптот.
А тепер переконаємося, що при у графіка теж немає похилій асимптоти. Для розкриття невизначеності використовуємо правило Лопіталя:
, Що і було потрібно перевірити.
При функція необмежено зростає, проте не існує такої прямої, до якої б її графік наближався нескінченно близько.
Переходимо до практичної частини уроку:
Як знайти асимптоти графіка функції?
Саме так формулюється типове завдання, і воно передбачає перебування ВСІХ асимптот графіка (вертикальних, похилих / горизонтальних). Хоча, якщо бути більш точним в постановці питання - мова йде про дослідження на наявність асимптот (адже таких може і зовсім не бути). Почнемо з чогось простого:
приклад 1
Знайти асимптоти графіка функції
Рішення зручно розбити на два пункти:
1) Спочатку перевіряємо, чи є вертикальні асимптоти. Знаменник звертається в нуль при, і відразу зрозуміло, що в даній точці функція терпить нескінченний розрив, А пряма, задана рівнянням, є вертикальною асимптотой графіка функції. Але, перш ніж оформити такий висновок, необхідно знайти односторонні межі: 
Нагадую техніку обчислень, на якій я подібно зупинявся в статті Безперервність функції. точки розриву. У вираз під знаком межі замість «ікси» підставляємо. У чисельнику нічого цікавого:
.
А ось в знаменнику виходить нескінченно мале негативне число:
, Воно і визначає долю межі.
Лівобічний межа нескінченний, і, в принципі вже можна винести вердикт про наявність вертикальної асимптоти. Але односторонні межі потрібні не тільки для цього - вони ДОПОМАГАЮТЬ ЗРОЗУМІТИ, ЯКрозташований графік функції і побудувати його кОРЕКТНО. Тому обов'язково обчислимо і правобічний межа: 
висновок: Односторонні межі нескінченні, значить, пряма є вертикальною асимптотой графіка функції при.
перший межа кінцевий, Значить, необхідно «продовжити розмову» і знайти другий межа:
Другий межа теж кінцевий.
Таким чином, наша асимптота:
висновок: Пряма, задана рівнянням є горизонтальною асимптотой графіка функції при.
Для знаходження горизонтальної асимптоти
можна користуватися спрощеною формулою:
якщо існує кінцевий межа, то пряма є горизонтальною асимптотой графіка функції при.
Неважко помітити, що чисельник і знаменник функції одного порядку зростання, А значить, шуканий межа буде кінцевим: 
відповідь:
За умовою не потрібно виконувати креслення, але якщо в самому розпалі дослідження функції, То на чернетці відразу ж робимо начерк: 
Виходячи з трьох знайдених меж, спробуйте самостійно прикинути, як може розташовуватися графік функції. Зовсім важко? Знайдіть 5-6-7-8 точок і відзначте їх на кресленні. Втім, графік даної функції будується за допомогою перетворень графіка елементарної функції, І читачі, уважно розглянули Приклад 21 зазначеної статті легко здогадаються, що це за крива.
приклад 2
Знайти асимптоти графіка функції
Це приклад для самостійного рішення. Процес, нагадую, зручно розбити на два пункти - вертикальні асимптоти і похилі асимптоти. У зразку рішення горизонтальна асимптота знайдена за спрощеною схемою.
На практиці найчастіше зустрічаються дрібно-раціональні функції, і після тренування на гіпербола усложним завдання:
приклад 3
Знайти асимптоти графіка функції 
Рішення: Раз, два і готово:
1) Вертикальні асимптоти знаходяться в точках нескінченного розриву, Тому потрібно перевірити, чи звертається знаменник в нуль. вирішимо квадратне рівняння:
Дискримінант позитивний, тому рівняння має два дійсних кореня, і роботи значно додається \u003d) 
З метою подальшого перебування односторонніх меж квадратний тричлен зручно розкласти на множники:
(Для компактного запису «мінус» внесли в першу дужку). Для підстраховки виконаємо перевірку, подумки або на чернетці розкривши дужки.
Перепишемо функцію у вигляді 
Знайдемо односторонні межі в точці: 
І в точці: 
Таким чином, прямі є вертикальними асимптотами графіка даної функції.
2) Якщо подивитися на функцію 
, То абсолютно очевидно, що межа буде кінцевим і у нас горизонтальна асимптота. Покажемо її наявність коротким способом: 
Таким чином, пряма (вісь абсцис) є горизонтальною асимптотой графіка даної функції.
відповідь:
Знайдені межі і асимптоти дають чимало інформації про графік функції. Постарайтеся подумки уявити креслення з урахуванням наступних фактів: 
Схематично зобразіть вашу версію графіка на чернетці.
Звичайно, знайдені межі однозначно не визначають вид графіка, і можливо, ви допустите помилку, але саме вправу надасть неоціненну допомогу в ході повного дослідження функції. Правильна картинка - в кінці уроку.
приклад 4
Знайти асимптоти графіка функції
приклад 5
Знайти асимптоти графіка функції 
Це завдання для самостійного рішення. Обидва графіка знову мають горизонтальними асимптотами, які негайно детектируются за такими ознаками: в Прімері 4 порядок зростання знаменника більше, Ніж порядок зростання чисельника, а в Примері 5 чисельник і знаменник одного порядку зростання. У зразку рішення перша функція досліджена на наявність похилих асимптот повним шляхом, а друга - через межу.
Горизонтальні асимптоти, на мою суб'єктивну враженню, зустрічаються помітно частіше, ніж ті, які «по-справжньому нахилені». Довгоочікуваний загальний випадок:
приклад 6
Знайти асимптоти графіка функції 
Рішення: класика жанру:
1) Оскільки знаменник позитивний, то функція неперервна на всій числовій прямій, і вертикальні асимптоти відсутні. ... Чи добре це? Не те слово - відмінно! Пункт №1 закритий.
2) Перевіримо наявність похилих асимптот:
перший межа кінцевий, Тому їдемо далі. В ході обчислення другого межі для усунення невизначеності «нескінченність мінус нескінченність» наводимо вислів до спільного знаменника: 
Другий межа теж кінцевий, Отже, у графіка даної функції існує похила асимптота:
висновок:
Таким чином, при графік функції 
нескінченно близько наближається до прямої: 
Зауважте, що він перетинає свою похилу асимптоту на початку координат, і такі точки перетину цілком припустимі - важливо, щоб «все було нормально» на нескінченності (власне, мова про асимптоти і заходить саме там).
приклад 7
Знайти асимптоти графіка функції
Рішення: Коментувати особливо нічого, тому оформлю приблизний зразок чистового рішення:
1) Вертикальні асимптоти. Досліджуємо точку.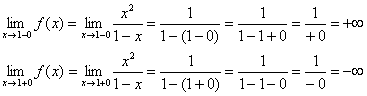 
Пряма є вертикальною асимптотой для графіка при.
2) Похилі асимптоти: 
Пряма є похилій асимптотой для графіка при.
відповідь: 
Найдьонов односторонні межі і асимптоти з високою вірогідністю дозволяють припустити, як виглядає графік даної функції. Коректний креслення в кінці уроку.
приклад 8
Знайти асимптоти графіка функції
Це приклад для самостійного рішення, для зручності обчислення деяких меж можна почленно розділити чисельник на знаменник. І знову, аналізуючи отримані результати, постарайтеся накреслити графік даної функції.
Очевидно, що володарями «справжніх» похилих асимптот є графіки тих дрібно-раціональних функцій, у яких старша ступінь чисельника на одиницю більше старшого ступеня знаменника. Якщо більше - похилій асимптоти вже не буде (наприклад,).
Але в житті відбуваються і інші чудеса:
приклад 9
приклад 11
Дослідити графік функції на наявність асимптот
Рішення: очевидно, що 
, Тому розглядаємо тільки праву полуплоскость, де є графік функції.
Таким чином, пряма (вісь ординат) є вертикальною асимптотой для графіка функції при.
2) Дослідження на похилу асимптоту можна провести за повною схемою, але в статті Правила Лопіталя ми з'ясували, що лінійна функція вищого порядку зростання, ніж логарифмічна, отже: 
(Див. Приклад 1 того ж уроку).
Висновок: вісь абсцис є горизонтальною асимптотой графіка функції при.
відповідь:
, Якщо;
, Якщо.
Креслення для наочності: 
Цікаво, що у начебто схожою функції асимптот немає взагалі (бажаючі можуть це перевірити).
Два заключних прикладу для самостійного вивчення:
приклад 12
Дослідити графік функції на наявність асимптот 
- поняття асимптот
Одним з важливих етапів побудови графіків функцій є пошук асимптот. З асимптотами ми зустрічалися неодноразово: при побудові графіків функцій, y \u003d tgx, y \u003d сtgx. Ми визначали їх як лінії, до яких «прагне» графік функції, але ніколи їх не перетне. Прийшов час дати точне визначення асимптот.
Асимптоти бувають трьох видів: вертикальна, горизонтальна і похила. На кресленні асимптоти прийнято позначати пунктирними лініями.
Розглянемо наступний штучно складений графік функції (рис. 16.1), на прикладі якого добре видно всі види асимптот:
Дамо визначення кожним видом асимптот:
1. Пряма х \u003d а називається вертикальної асимптотой функції, якщо.
2. Пряма у \u003d з називається горизонтальної асимптотой функції, якщо.
3. Пряма у \u003d kx + bназивається похилій асимптотой функції, якщо.
Геометрично визначення похилій асимптоти означає, що при → ∞ графік функції як завгодно близько підходить до прямої у \u003d kx + b, Тобто вони практично збігаються. Різниця практично однакових виразів прагне до нуля.
Відзначимо, що горизонтальні та похилі асимптоти розглядаються тільки за умови → ∞. Іноді їх розрізняють на горизонтальні і похилі асимптоти при → + ∞ і → -∞.
- Алгоритм пошуку асимптот
Для пошуку асимптот можна використовувати наступний алгоритм:
Вертикальних асимптот може бути одна, кілька чи не бути зовсім.
- Якщо з - число, то у \u003d з - горизонтальна асимптота;
- Якщо з - нескінченність, то горизонтальних асимптот немає.
Якщо функція являє собою відношення двох многочленів, то при наявності у функції горизонтальних асимптот похилі асимптоти шукати не будемо - їх немає.
Розглянемо приклади знаходження асимптот функції:
Приклад 16.1. Знайдіть асимптоти кривої.
Рішення х-1≠0; х≠1.
Перевіримо, чи є пряма х \u003d1 вертикальної асимптотой. Для цього обчислимо межа функції в точці х \u003d1: .
х \u003d1 - вертикальна асимптота.
з= .
з\u003d \u003d. Оскільки з\u003d 2 (число), то у \u003d 2 - горизонтальна асимптота.
Так як функція являє собою відношення многочленів, то при наявності горизонтальних асимптот стверджуємо, що похилих асимптот немає.
х \u003d1 і горизонтальну асимптоти у \u003d 2.Для наочності графік даної функції представлений на рис. 16.2.
приклад 16.2. Знайдіть асимптоти кривої.
Рішення. 1. Знайдемо область визначення функції: х-2≠0; х≠2.
Перевіримо, чи є пряма х \u003d2 вертикальної асимптотой. Для цього обчислимо межа функції в точці х \u003d2: .
Отримали, що, отже, х \u003d2 - вертикальна асимптота.
2. Для пошуку горизонтальних асимптот знаходимо: з= .
Оскільки в межі фігурує невизначеність, скористаємося правилом Лопіталя: з\u003d \u003d. Оскільки з- нескінченність, то горизонтальних асимптот немає.
3. Для пошуку похилих асимптот знаходимо:
Отримали невизначеність виду, скористаємося правилом Лопіталя: \u003d \u003d 1.Ітак, 1. Знайдемо bза формулою: .
b \u003d = =
Отримали, що b \u003d 2. Тоді у \u003d kx + b -похила асимптота. У нашому випадку вона має вигляд: у \u003d x + 2.
|
Контрольні питання:
Лекція 17. ЗАГАЛЬНА СХЕМА ДОСЛІДЖЕННЯ ФУНКЦІЇ І ПОБУДОВИ ГРАФІКА
У даній лекції ми підведемо підсумок всьому раніше вивченого матеріалу. Кінцева мета нашого довгого шляху - вміти досліджувати будь-яку аналітично задану функцію і будувати її графік. Важливими ланками нашого дослідження будуть дослідження функції на екстремуми, визначення інтервалів монотонності, опуклості і угнутості графіка, пошук точок перегину, асимптот графіка функції.
З урахуванням всіх перерахованих вище аспектів наведемо схему дослідження функції та побудови графіка .
1. Знайти область визначення функції.
2. Дослідити функцію на парність-непарність:
· Якщо, то функція парна (графік парної функції симетричний щодо осі Оу);
· Якщо, то функція непарна (графік непарної функції симетричний відносно початку координат);
· В іншому випадку функція ні парна, ні непарна.
3. Дослідити функцію на періодичність (серед досліджуваних нами функцій періодичними можуть бути тільки тригонометричні функції).
4. Знайти точки перетину графіка функції з осями координат:
· Ох: у\u003d 0 (вирішуємо рівняння лише в тому випадку, якщо можемо використовувати відомі нам методи);
· Оу: х=0.
5. Знайти першу похідну функції і критичні точки першого роду.
6. Знайти інтервали монотонності і екстремуми функції.
7. Знайти другу похідну функції і критичні точки другого роду.
8. Знайти інтервали опуклості-угнутості графіка функції та точки перегину.
9. Знайти асимптоти графіка функції.
10. Побудувати графік функції. При побудові слід врахувати випадки можливого розташування графіка поблизу асимптот :
11. При необхідності вибрати контрольні точки для більш точного побудови.
Розглянемо схему дослідження функції та побудови її графіка на конкретних прикладах:
приклад 17.1. Побудуйте графік функції.
Рішення. 1. Ця функція визначена на всій числовій прямій за винятком х\u003d 3, тому що в цій точці знаменник звертається в нуль.
2. Для визначення парності і непарності функції знайдемо:
Бачимо, що і, отже, функція ні парна, ні непарна.
3. Функція неперіодичних.
4. Знайдемо точки перетину з осями координат. Для знаходження точки перетину з віссю Ох приймемо у\u003d 0. Отримаємо рівняння:. Отже, точка (0; 0) - точка перетину з осями координат.
5. Знайдемо похідну функції за правилом диференціювання дробу: \u003d \u003d \u003d \u003d.
Для знаходження критичних точок знайдемо точки, в яких похідна функції дорівнює 0 або не існує.
Якщо \u003d 0, отже,. Твір тоді дорівнює 0, коли хоча б один із множників дорівнює 0: або.
х-3) 2 дорівнює 0, тобто не існує при х=3.
Отже, функція має три критичні точки першого роду:; ; .
6. На числової осі відзначимо критичні точки першого роду, причому точку відзначаємо виколоти точкою, тому що в ній функція не визначена.
Розставляємо знаки похідної \u003d на кожному проміжку:
|
|
На проміжках, де, початкова функція зростає (при (-∞; 0]), де - убуває (при).
Крапка х\u003d 0 є точкою максимуму функції. Для знаходження максимуму функції знайдемо значення функції в точці 0:.
Крапка х\u003d 6 є точкою мінімуму функції. Для знаходження мінімуму функції знайдемо значення функції в точці 6:.
Результати досліджень можна занести в таблицю. Число рядків в таблиці фіксоване і дорівнює чотирьом, а число стовпців залежить від досліджуваної функції. В осередку першого рядка послідовно заносять інтервали, на які критичні точки розбивають область визначення функції, включаючи самі критичні точки. Щоб уникнути помилок при побудові точки, які не належать області визначення, можна в таблицю не включати.
У другому рядку таблиці розставляються знаки похідної на кожному з розглянутих проміжків і значення похідної в критичних точках. Відповідно до знаками похідної функції в третьому рядку відзначаються проміжки зростання, спадання, екстремуми функції.
Останній рядок служить для позначення максимуму і мінімуму функції.
| х | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f (x) | |||||||
| висновки | max | min |
7. Знайдемо другу похідну функції як похідну від першої похідної: \u003d \u003d
Винесемо в чисельнику х-3 за дужки і виконаємо скорочення:
Наведемо в чисельнику подібні доданки:.
Знайдемо критичні точки другого роду: точки, в яких друга похідна функції дорівнює нулю або не існує.
0, якщо \u003d 0. Дана дріб не може дорівнювати нулю, отже, точок, в яких друга похідна функції дорівнює нулю, немає.
Не існує, якщо знаменник ( х-3) 3 дорівнює 0, тобто не існує при х\u003d 3. : Ох, Оу, Початок відліку, одиниці вимірювання по кожній осі.
Перш ніж будувати графік функції, потрібно:
· Провести асимптоти пунктирними лініями;
· Відзначити точки перетину з осями координат;
|
· Користуючись отриманими даними про проміжках зростання, убування, опуклості і угнутості, побудувати графік функції. Гілки графіка повинні «прагнути» до асимптотам, але їх не перетинати.
· Перевірити, чи відповідає графік функції з проведеним дослідженням: якщо функція парна або непарна, то дотримана симетрія; чи відповідають теоретично знайденим проміжки зростання та спадання, опуклості і угнутості, точки перегину.
11. Для більш точного побудови можна вибрати кілька контрольних точок. Наприклад, знайдемо значення функції в точках 2 і 7:
Коригуємо графік з урахуванням контрольних точок.
Контрольні питання:
- Який алгоритм побудови графіка функції?
- Чи може функція мати екстремум в точках, які не належать області визначення?
ГЛАВА 3. 3. інтегрального числення Функції
Рішення зручно розбити на два пункти:
1) Спочатку перевіряємо, чи є вертикальні асимптоти. Знаменник звертається в нуль при, і відразу зрозуміло, що в даній точці функція терпить нескінченний розрив, а пряма, задана рівнянням, є вертикальною асимптотой графіка функції. Але, перш ніж оформити такий висновок, необхідно знайти односторонні межі:
Нагадую техніку обчислень, на якій я подібно зупинявся в статті Безперервність функції. Точки розриву. У вираз під знаком межі замість «ікси» підставляємо. У чисельнику нічого цікавого:
А ось в знаменнику виходить нескінченно мале негативне число:
Воно і визначає долю межі.
Лівобічний межа нескінченний, і, в принципі вже можна винести вердикт про наявність вертикальної асимптоти. Але односторонні межі потрібні не тільки для цього - вони ДОПОМАГАЮТЬ ЗРОЗУМІТИ, ЯК розташований графік функції і побудувати його коректно. Тому обов'язково обчислимо і правобічний межа:
Висновок: односторонні межі нескінченні, значить, пряма є вертикальною асимптотой графіка функції при.
Перший межа кінцевий, значить, необхідно «продовжити розмову» і знайти другий межа:
Другий межа теж кінцевий.
Таким чином, наша асимптота:
Висновок: пряма, задана рівнянням є горизонтальною асимптотой графіка функції при.
Для знаходження горизонтальної асимптоти можна користуватися спрощеною формулою:
Якщо існує кінцевий межа, то пряма є горизонтальною асимптотой графіка функції при.
Неважко помітити, що чисельник і знаменник функції одного порядку зростання, а значить, шуканий межа буде кінцевим:
За умовою не потрібно виконувати креслення, але якщо в самому розпалі дослідження функції, то на чернетці відразу ж робимо начерк:
Виходячи з трьох знайдених меж, спробуйте самостійно прикинути, як може розташовуватися графік функції. Зовсім важко? Знайдіть 5-6-7-8 точок і відзначте їх на кресленні. Втім, графік даної функції будується за допомогою перетворень графіка елементарної функції, і читачі, уважно розглянули Приклад 21 зазначеної статті легко здогадаються, що це за крива.
Це приклад для самостійного рішення. Процес, нагадую, зручно розбити на два пункти - вертикальні асимптоти і похилі асимптоти. У зразку рішення горизонтальна асимптота Найдьонов за спрощеною схемою.
На практиці найчастіше зустрічаються дрібно-раціональні функції, і після тренування на гіпербола усложним завдання:
Знайти асимптоти графіка функції
Рішення: Раз, два і готово:
1) Вертикальні асимптоти знаходяться в точках нескінченного розриву, тому потрібно перевірити, чи звертається знаменник в нуль. Вирішимо квадратне рівняння:
Дискримінант позитивний, тому рівняння має два дійсних кореня, і роботи значно додається
З метою подальшого перебування односторонніх меж квадратний тричлен зручно розкласти на множники:
(Для компактного запису «мінус» внесли в першу дужку). Для підстраховки виконаємо перевірку, подумки або на чернетці розкривши дужки.
Перепишемо функцію у вигляді
Знайдемо односторонні межі в точці:
асимптота графік функція межа
І в точці:
Таким чином, прямі є вертикальними асимптотами графіка даної функції.
2) Якщо подивитися на функцію, то абсолютно очевидно, що межа буде кінцевим і у нас горизонтальна асимптота. Покажемо її наявність коротким способом:
Таким чином, пряма (вісь абсцис) є горизонтальною асимптотой графіка даної функції.
Знайдені межі і асимптоти дають чимало інформації про графік функції. Постарайтеся подумки уявити креслення з урахуванням наступних фактів:
Схематично зобразіть вашу версію графіка на чернетці.
Звичайно, знайдені межі однозначно не визначають вид графіка, і можливо, ви допустите помилку, але саме вправу надасть неоціненну допомогу в ході повного дослідження функції. Правильна картинка - в кінці уроку.
Знайти асимптоти графіка функції
Знайти асимптоти графіка функції
Це завдання для самостійного рішення. Обидва графіка знову мають горизонтальними асимптотами, які негайно детектируются за такими ознаками: в Прімері 4порядок зростання знаменника більше, ніж порядок зростання чисельника, а в Примері 5 чисельник і знаменник одного порядку зростання. У зразку рішення перша функція досліджена на наявність похилих асимптот повним шляхом, а друга - через межу.
Горизонтальні асимптоти, на мою суб'єктивну враженню, зустрічаються помітно частіше, ніж ті, які «по-справжньому нахилені». Довгоочікуваний загальний випадок:
Знайти асимптоти графіка функції
Рішення: класика жанру:
- 1) Оскільки знаменник позитивний, то функція неперервна на всій числовій прямій, і вертикальні асимптоти відсутні. ... Чи добре це? Не те слово - відмінно! Пункт №1 закритий.
- 2) Перевіримо наявність похилих асимптот:
Другий межа теж кінцевий, отже, у графіка даної функції існує похила асимптота:
Таким чином, при графік функції нескінченно близько наближається до прямої.
Зауважте, що він перетинає свою похилу асимптоту на початку координат, і такі точки перетину цілком припустимі - важливо, щоб «все було нормально» на нескінченності (власне, мова про асимптоти і заходить саме там).
Знайти асимптоти графіка функції
Рішення: коментувати особливо нічого, тому оформлю приблизний зразок чистового рішення:
1) Вертикальні асимптоти. Досліджуємо точку.
Пряма є вертикальною асимптотой для графіка при.
2) Похилі асимптоти:
Пряма є похилій асимптотой для графіка при.
Найдьонов односторонні межі і асимптоти з високою вірогідністю дозволяють припустити, як виглядає графік даної функції.
Знайти асимптоти графіка функції
Це приклад для самостійного рішення, для зручності обчислення деяких меж можна почленно розділити чисельник на знаменник. І знову, аналізуючи отримані результати, постарайтеся накреслити графік даної функції.
Очевидно, що володарями «справжніх» похилих асимптот є графіки тих дрібно-раціональних функцій, у яких старша ступінь чисельника на одиницю більше старшого ступеня знаменника. Якщо більше - похилій асимптоти вже не буде (наприклад,).
Але в житті відбуваються і інші чудеса.
Будуть і завдання для самостійного рішення, до яких можна подивитися відповіді.
поняття асимптоти
Якщо попередньо побудувати асимптоти кривої, то багатьох випадках побудова графіка функції полегшується.
Доля асимптоти сповнена трагізму. Уявіть собі, яке це: все життя рухатися по прямій до заповітної мети, підійти до неї максимально близько, але так і не досягти її. Наприклад, прагнути з'єднати свій життєвий шлях з шляхом бажаної людини, в якийсь момент наблизитися до нього майже впритул, але навіть не торкнутися його. Або прагнути заробити мільярд, але до досягнення цієї мети і записи в книгу рекордів Гіннеса для свого нагоди не дістає сотих часток цента. І тому подібне. Так і з асимптотой: вона постійно прагне досягти кривої графіка функції, наближається до нього на мінімальну можливу відстань, але так і не стосується його.
Визначення 1. асимптотами називаються такі прямі, до яких як завгодно близько наближається графік функції, коли змінна прагне до плюс нескінченності або до мінус нескінченності.
Визначення 2. Пряма називається асимптотой графіка функції, якщо відстань від змінної точки М графіка функції до цієї прямої прямує до нуля при необмеженому видаленні точки М від початку координат з якої-небудь гілки графіка функції.
Розрізняють три види асимптот: вертикальні, горизонтальні і похилі.
вертикальні асимптоти
Перше, що потрібно дізнатися про вертикальних асимптот: вони паралельні осі Oy .
визначення. пряма x = a є вертикальної асимптотой графіка функції , Якщо точка x = a є точкою розриву другого роду для цієї функції.
З визначення випливає, що пряма x = a є вертикальною асимптотой графіка функції f(x), Якщо виконується хоча б одна з умов:
При цьому функція f(x) Може бути взагалі не визначена відповідно при x ≥ a і x ≤ a .
зауваження:
Приклад 1.Графік функції y\u003d ln x має вертикальну асимптоту x \u003d 0 (тобто збігається з віссю Oy ) На кордоні області визначення, так як межа функції при прагненні ікси до нуля праворуч дорівнює мінус нескінченності:
(Рис. Зверху).
самостійно, а потім подивитися рішення
Приклад 2.Знайти асимптоти графіка функції.
Приклад 3.Знайти асимптоти графіка функції
горизонтальні асимптоти
Перше, що потрібно дізнатися про горизонтальних асимптот: вони паралельні осі Ox .
Якщо (межа функції при прагненні аргументу до плюс або мінус нескінченності дорівнює деякому значенню b), То y = b – горизонтальна асимптота кривої y = f(x ) (Права при ІКСІ, які прагнуть до плюс нескінченності, ліва при ІКСІ, які прагнуть до мінус нескінченності, і двостороння, якщо межі при прагненні ікси до плюс або мінус нескінченності рівні).
Приклад 5.Графік функції
при a \u003e 1 має ліву горизонтальну асімпототу y \u003d 0 (тобто збігається з віссю Ox ), Так як межа функції при прагненні "ікси" до мінус нескінченності дорівнює нулю:
Правою горизонтальної асимптоти у кривої немає, оскільки межа функції при прагненні "ікси" до плюс нескінченності дорівнює нескінченності:
похилі асимптоти
Вертикальні і горизонтальні асимптоти, які ми розглянули вище, паралельні осях координат, тому для їх побудови нам потрібно лише певне число - точка на осі абсцис або ординат, через яку проходить асимптота. Для похилій асимптоти необхідно більше - кутовий коефіцієнт k, Який показує кут нахилу прямої, і вільний член b, Який показує, наскільки пряма знаходиться вище або нижче початку координат. Чи не встигли забути аналітичну геометрію, а з неї - рівняння прямої, помітять, що для похилої асимптоти знаходять рівняння прямої з кутовим коефіцієнтом . Існування похилій асимптоти визначається наступною теоремою, на підставі якої і знаходять названі тільки що коефіцієнти.
Теорема.Для того, щоб крива y = f(x) мала асимптоту y = kx + b , Необхідно і достатньо, щоб існували кінцеві межі k і b розглянутої функції при прагненні змінної x до плюс нескінченності і мінус нескінченності:
(1)
(2)
Знайдені таким чином числа k і b і є коефіцієнтами похилій асимптоти.
У першому випадку (при прагненні ікси до плюс нескінченності) виходить права похила асимптота, у другому (при прагненні ікси до мінус нескінченності) - ліва. Права похила асимптота зображена на рис. знизу.
При знаходженні рівняння похилій асимптоти необхідно враховувати прагнення ікси і до плюс нескінченності, і до мінус нескінченності. У деяких функцій, наприклад, у дрібно-раціональних, ці межі збігаються, однак у багатьох функцій ці межі різні а також може існувати тільки один з них.
При збігу меж при ІКСІ, яка прагне до плюс нескінченності і до мінус нескінченності пряма y = kx + b є двосторонньою асимптотой кривої.
Якщо хоча б один з меж, що визначають асимптоту y = kx + b , Не існує, то графік функції не має похилій асимптоти (але може мати вертикальну).
Неважко бачити, що горизонтальна асимптота y = b є окремим випадком похилої y = kx + b при k = 0 .
Тому якщо в будь-якому напрямку крива має горизонтальну асимптоти, то в цьому напрямку немає похилій, і навпаки.
Приклад 6.Знайти асимптоти графіка функції
Рішення. Функція визначена на всій числовій прямій, крім x \u003d 0, тобто
Тому в точці розриву x \u003d 0 крива може мати вертикальну асимптоту. Дійсно, межа функції при прагненні ікси до нуля зліва дорівнює плюс нескінченності:
отже, x \u003d 0 - вертикальна асимптота графіка даної функції.
Горизонтальної асимптоти графік даної функції не має, так як межа функції при прагненні ікси до плюс нескінченності дорівнює плюс нескінченності:
З'ясуємо наявність похилої асимптоти:
Отримали кінцеві межі k \u003d 2 і b \u003d 0. пряма y = 2x є двосторонньою похилій асимптотой графіка даної функції (рис. усередині прикладу).
Приклад 7.Знайти асимптоти графіка функції
Рішення. Функція має одну точку розриву x \u003d -1. Обчислимо односторонні межі і визначимо вид розриву:
висновок: x \u003d -1 - точка розриву другого роду, тому пряма x \u003d -1 є вертикальною асимптотой графіка даної функції.
Шукаємо похилі асимптоти. Так як дана функція - дрібно-раціональна, межі при і при збігатимуться. Таким чином, знаходимо коефіцієнти для підстановки в рівняння прямої - похилій асимптоти:
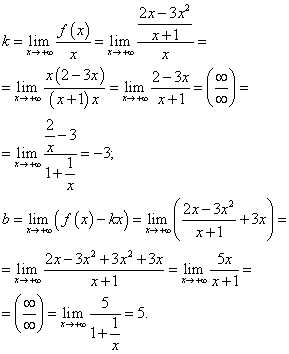
Підставляючи знайдені коефіцієнти в рівняння прямої з кутовим коефіцієнтом, отримуємо рівняння похилій асимптоти:
y = −3x + 5 .
На малюнку графік функції позначений бордовим кольором, а асимптоти - чорним.
Приклад 8.Знайти асимптоти графіка функції
Рішення. Так як дана функція неперервна, її графік не має вертикальних асимптот. Шукаємо похилі асимптоти:
.
Таким чином, графік даної функції має асимптоту y \u003d 0 при і не має асіптоти прі.
Приклад 9.Знайти асимптоти графіка функції
Рішення. Спочатку шукаємо вертикальні асимптоти. Для цього знайдемо область визначення функції. Функція визначена, коли виконується нерівність і при цьому. знак змінної x збігається зі знаком. Тому розглянемо еквівалентну нерівність. З цього отримуємо область визначення функції: 
. Вертикальна асимптота може бути тільки на кордоні області визначення функції. але x \u003d 0 не може бути вертикальної асимптотой, так як функція визначена при x = 0
.
Розглянемо правобічний межа при (лівобічний межа не існує):
.
Крапка x \u003d 2 - точка розриву другого роду, тому пряма x \u003d 2 - вертикальна асимптота графіка даної функції.
Шукаємо похилі асимптоти:
Отже, y = x + 1 - похила асимптота графіка даної функції при. Шукаємо похилу асимптоту при:
Отже, y = −x − 1 - похила асимптота при.
Приклад 10.Знайти асимптоти графіка функції
Рішення. Функція має область визначення 
. Так як вертикальна асимптота графіка цієї функції може бути тільки на кордоні області визначення, знайдемо односторонні межі функції при.
Саме так формулюється типове завдання, і воно передбачає перебування ВСІХ асимптот графіка (вертикальних, похилих / горизонтальних). Хоча, якщо бути більш точним в постановці питання - мова йде про дослідження на наявність асимптот (адже таких може і зовсім не бути).
Почнемо з чогось простого:
приклад 1
Рішення зручно розбити на два пункти:
1) Спочатку перевіряємо, чи є вертикальні асимптоти. Знаменник звертається в нуль при, і відразу зрозуміло, що в даній точці функція терпить нескінченний розрив, А пряма, задана рівнянням, є вертикальною асимптотой графіка функції. Але, перш ніж оформити такий висновок, необхідно знайти односторонні межі: 
Нагадую техніку обчислень, на якій я подібно зупинявся в статті безперервність функції. точки розриву. У вираз під знаком межі замість «ікси» підставляємо. У чисельнику нічого цікавого:
.
А ось в знаменнику виходить нескінченно мале негативне число:
, Воно і визначає долю межі.
Лівобічний межа нескінченний, і, в принципі вже можна винести вердикт про наявність вертикальної асимптоти. Але односторонні межі потрібні не тільки для цього - вони ДОПОМАГАЮТЬ ЗРОЗУМІТИ, ЯКрозташований графік функції і побудувати його кОРЕКТНО. Тому обов'язково обчислимо і правобічний межа: 
висновок: Односторонні межі нескінченні, значить, пряма є вертикальною асимптотой графіка функції при.
перший межа кінцевий, Значить, необхідно «продовжити розмову» і знайти другий межа:
Другий межа теж кінцевий.
Таким чином, наша асимптота:
висновок: Пряма, задана рівнянням є горизонтальною асимптотой графіка функції при.
Для знаходження горизонтальної асимптоти можна користуватися спрощеною формулою:
Якщо існує кінцевий межа, то пряма є горизонтальною асимптотой графіка функції при.
Неважко помітити, що чисельник і знаменник функції одного порядку зростання, А значить, шуканий межа буде кінцевим: 
відповідь:
За умовою не потрібно виконувати креслення, але якщо в самому розпалі дослідження функції, То на чернетці відразу ж робимо начерк: 
Виходячи з трьох знайдених меж, спробуйте самостійно прикинути, як може розташовуватися графік функції. Зовсім важко? Знайдіть 5-6-7-8 точок і відзначте їх на кресленні. Втім, графік даної функції будується за допомогою перетворень графіка елементарної функції, І читачі, уважно розглянули Приклад 21 зазначеної статті легко здогадаються, що це за крива.
приклад 2
Знайти асимптоти графіка функції
Це приклад для самостійного рішення. Процес, нагадую, зручно розбити на два пункти - вертикальні асимптоти і похилі асимптоти. У зразку рішення горизонтальна асимптота Найдьонов за спрощеною схемою.
На практиці найчастіше зустрічаються дрібно-раціональні функції, і після тренування на гіпербола усложним завдання:
приклад 3
Знайти асимптоти графіка функції 
Рішення: Раз, два і готово:
1) Вертикальні асимптоти знаходяться в точках нескінченного розриву, Тому потрібно перевірити, чи звертається знаменник в нуль. вирішимо квадратне рівняння :
Дискримінант позитивний, тому рівняння має два дійсних кореня, і роботи значно додається \u003d) 
З метою подальшого перебування односторонніх меж квадратний тричлен зручно розкласти на множники:
(Для компактного запису «мінус» внесли в першу дужку). Для підстраховки виконаємо перевірку, подумки або на чернетці розкривши дужки.
Перепишемо функцію у вигляді 
Знайдемо односторонні межі в точці: 
І в точці: 
Таким чином, прямі є вертикальними асимптотами графіка даної функції.
2) Якщо подивитися на функцію 
, То абсолютно очевидно, що межа буде кінцевим і у нас горизонтальна асимптота. Покажемо її наявність коротким способом: 
Таким чином, пряма (вісь абсцис) є горизонтальною асимптотой графіка даної функції.
відповідь:
Знайдені межі і асимптоти дають чимало інформації про графік функції. Постарайтеся подумки уявити креслення з урахуванням наступних фактів: 
Схематично зобразіть вашу версію графіка на чернетці.
Звичайно, знайдені межі однозначно не визначають вид графіка, і можливо, ви допустите помилку, але саме вправу надасть неоціненну допомогу в ході повного дослідження функції. Правильна картинка - в кінці уроку.
приклад 4
Знайти асимптоти графіка функції
приклад 5
Знайти асимптоти графіка функції 
Це завдання для самостійного рішення. Обидва графіка знову мають горизонтальними асимптотами, які негайно детектируются за такими ознаками: в Прімері 4 порядок зростання знаменника більше, ніж порядок зростання чисельника, а в Примері 5 чисельник і знаменник одного порядку зростання. У зразку рішення перша функція досліджена на наявність похилих асимптот повним шляхом, а друга - через межу.
Горизонтальні асимптоти, на мою суб'єктивну враженню, зустрічаються помітно частіше, ніж ті, які «по-справжньому нахилені». Довгоочікуваний загальний випадок:
приклад 6
Знайти асимптоти графіка функції 
Рішення: класика жанру:
1) Оскільки знаменник позитивний, то функція неперервна на всій числовій прямій, і вертикальні асимптоти відсутні. ... Чи добре це? Не те слово - відмінно! Пункт №1 закритий.
2) Перевіримо наявність похилих асимптот:
перший межа кінцевий, Тому їдемо далі. В ході обчислення другого межі для усунення невизначеності «нескінченність мінус нескінченність» наводимо вислів до спільного знаменника: 
Другий межа теж кінцевий, Отже, у графіка даної функції існує похила асимптота:
висновок:
Таким чином, при графік функції нескінченно близько наближається до прямої: 
Зауважте, що він перетинає свою похилу асимптоту на початку координат, і такі точки перетину цілком припустимі - важливо, щоб «все було нормально» на нескінченності (власне, мова про асимптоти і заходить саме там).
приклад 7
Знайти асимптоти графіка функції
Рішення: Коментувати особливо нічого, тому оформлю приблизний зразок чистового рішення:
1) Вертикальні асимптоти. Досліджуємо точку. 
Пряма є вертикальною асимптотой для графіка при.
2) Похилі асимптоти: 
Пряма є похилій асимптотой для графіка при.
відповідь: 
Найдьонов односторонні межі і асимптоти з високою вірогідністю дозволяють припустити, як виглядає графік даної функції. Коректний креслення в кінці уроку.
приклад 8
Знайти асимптоти графіка функції
Це приклад для самостійного рішення, для зручності обчислення деяких меж можна почленно розділити чисельник на знаменник. І знову, аналізуючи отримані результати, постарайтеся накреслити графік даної функції.
Очевидно, що володарями «справжніх» похилих асимптот є графіки тих дрібно-раціональних функцій, у яких старша ступінь чисельника на одиницю більше старшого ступеня знаменника. Якщо більше - похилій асимптоти вже не буде (наприклад,).
Але в житті відбуваються і інші чудеса:
приклад 9
Рішення: функція неперервна на всій числовій прямій, значить, вертикальні асимптоти відсутня. Але ось похилі цілком можуть бути. перевіряємо:
Пригадую, як ще в інституті зіткнувся зі схожою функцією і просто не міг повірити, що у неї є похила асимптота. До тих пір, поки не вирахував другий межа:
Строго кажучи, тут дві невизначеності: і, але так чи інакше, потрібно використовувати метод вирішення, який розібраний в прикладах 5-6 статті про межах підвищеної складності. Множимо і ділимо на поєднане вираз, щоб скористатися формулою:
відповідь:
Мабуть, найпопулярніша похила асимптота.
До сих пір нескінченності вдавалося «стригти під одну гребінку», але буває, що у графіка функції дві різні похилі асимптоти при і при:
приклад 10
Дослідити графік функції на наявність асимптот 
Рішення: Подкоренное вираз позитивно, значить, область визначення - будь-який дійсно число, і вертикальних палиць бути не може.
Перевіримо, чи існують похилі асимптоти.
Якщо «ікс» прагне до «мінус нескінченності», то:
(При внесенні «ікси» під квадратний корінь необхідно додати знак «мінус», щоб не втратити негативність знаменника)
Виглядає незвично, але тут невизначеність «нескінченність мінус нескінченність». Множимо чисельник і знаменник на поєднане вираз:
Таким чином, пряма є похилою асимптотой графіка при.
З «плюс нескінченністю» все тривіальніше: 
А пряма - при.
відповідь:
якщо;
, Якщо.
Не утримаюся від графічного зображення: 
Це одна з гілок гіперболи .
Не рідкість, коли потенційна наявність асимптот спочатку обмежена областю визначення функції:
приклад 11
Дослідити графік функції на наявність асимптот
Рішення: очевидно, що 
, Тому розглядаємо тільки праву полуплоскость, де є графік функції.
1) Функція неперервна на інтервалі, а значить, якщо вертикальна асимптота і існує, то це може бути тільки вісь ординат. Досліджуємо поведінку функції поблизу точки справа:
Зверніть увагу, тут НІ невизначеності (На таких випадках акцентувалася увага на початку статті Методи вирішення меж).
Таким чином, пряма (вісь ординат) є вертикальною асимптотой для графіка функції при.
2) Дослідження на похилу асимптоту можна провести за повною схемою, але в статті Правила Лопітал ми з'ясували, що лінійна функція вищого порядку зростання, ніж логарифмічна, отже: 
(Див. Приклад 1 того ж уроку).
Висновок: вісь абсцис є горизонтальною асимптотой графіка функції при.
відповідь:
якщо;
, Якщо.
Креслення для наочності: 
Цікаво, що у начебто схожою функції асимптот немає взагалі (бажаючі можуть це перевірити).
Два заключних прикладу для самостійного вивчення:
приклад 12
Дослідити графік функції на наявність асимптот 
Для перевірки на вертикальні асимптоти спочатку потрібно знайти область визначення функції, А потім обчислити пару односторонніх меж в «підозрілих» точках. Похилі асимптоти теж не виключені, оскільки функція визначена на «плюс» і «мінус» нескінченності.
приклад 13
Дослідити графік функції на наявність асимптот
А тут можуть бути тільки похилі асимптоти, причому напрямки, слід розглянути окремо.
Сподіваюся, ви знайшли потрібну асимптоту \u003d)
Бажаю успіхів!
Рішення і відповіді:
Приклад 2:Рішення
:
. Знайдемо односторонні межі:
пряма є вертикальною асимптотой графіка функції при .
2) Похилі асимптоти.
пряма .
відповідь:
креслення
до Прикладу 3:
Приклад 4:Рішення
:
1) Вертикальні асимптоти. Функція терпить нескінченний розрив в точці . Обчислимо односторонні межі:
Примітка: Нескінченно мале негативне число в парному ступеня одно нескінченно малому позитивному числу: .
пряма є вертикальною асимптотой графіка функції.
2) Похилі асимптоти.
пряма (Вісь абсцис) є горизонтальною асимптотой графіка функції при .
відповідь:
