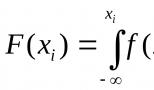Simulering av slumpmässiga händelser. Spelar en kontinuerlig slumpvariabel. Invers funktionsmetod Spela fem möjliga värden av en kontinuerlig slumpvariabel

Definition 24.1.Slumpmässiga siffror nämn möjliga värden r kontinuerlig slumpvariabel R, jämnt fördelat i intervallet (0; 1).

1. Spela en diskret slumpvariabel.

Anta att vi vill spela en diskret slumpvariabel X, det vill säga få en sekvens av dess möjliga värden, med kännedom om distributionslagen X:

X x 1 X 2 … x n

r r 1 R 2 … r sid .

Betrakta en slumpvariabel likformigt fördelad i (0, 1) R och dela intervallet (0, 1) med punkter med koordinater R 1, R 1 + R 2 , …, R 1 + R 2 +… +r sid-1 på P delintervall vars längder är lika med sannolikheterna med samma index.

Sats 24.1. Om varje slumptal som faller in i intervallet tilldelas ett möjligt värde, kommer värdet som spelas att ha en given distributionslag:

X x 1 X 2 … x n

r r 1 R 2 … r sid .

Bevis.

Möjliga värden för den resulterande slumpvariabeln sammanfaller med uppsättningen X 1 , X 2 ,… x n, eftersom antalet intervall är lika P, och när man träffar r j i ett intervall kan en slumpvariabel endast ta ett av värdena X 1 , X 2 ,… x n.

Därför att Rär jämnt fördelad, då är sannolikheten att den faller in i varje intervall lika med dess längd, vilket betyder att varje värde motsvarar sannolikheten p i. Således har den slumpmässiga variabeln som spelas en given distributionslag.

Exempel. Spela 10 värden av en diskret slumpvariabel X, vars distributionslag har formen: X 2 3 6 8

R 0,1 0,3 0,5 0,1

Lösning. Låt oss dela upp intervallet (0, 1) i delintervall: D 1 - (0; 0,1), D 2 - (0,1; 0,4), D 3 - (0,4; 0,9), D 4 – (0,9; 1). Låt oss skriva ut 10 tal från tabellen med slumptal: 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0,34. De första och sjunde siffrorna ligger på intervallet D 1, därför fick den spelade slumpvariabeln i dessa fall värdet X 1 = 2; det tredje, fjärde, åttonde och tionde numret föll i intervallet D 2, vilket motsvarar X 2 = 3; det andra, femte, sjätte och nionde numret låg i intervallet D 3 - i det här fallet X = x 3 = 6; Det fanns inga siffror under det senaste intervallet. Så de möjliga värdena spelade ut Xär: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. Utspela motsatta händelser.

Låt det krävas att spela ut tester, i varje en händelse A visas med känd sannolikhet R. Betrakta en diskret slumpvariabel X, med värdet 1 (om händelsen A hänt) med sannolikhet R och 0 (om A hände inte) med sannolikhet q = 1 – sid. Sedan kommer vi att spela denna slumpmässiga variabel som föreslagits i föregående stycke.

Exempel. Spela 10 utmaningar, var och en med en händelse A visas med sannolikhet 0,3.

Lösning. För en slumpvariabel X med distributionslagen X 1 0

R 0,3 0,7

får vi intervallen D 1 – (0; 0,3) och D 2 – (0,3; 1). Vi använder samma urval av slumptal som i föregående exempel, för vilka siffrorna nr 1, 3 och 7 faller i intervallet D 1, och resten - i intervallet D 2. Därför kan vi anta att händelsen A inträffade i de första, tredje och sjunde försöken, men inträffade inte i de återstående försöken.

3. Spela upp en komplett grupp av händelser.

Om händelser A 1 , A 2 , …, A sid, vars sannolikheter är lika R 1 , R 2 ,… r sid, bilda en komplett grupp, och sedan för lek (det vill säga modellera sekvensen av deras framträdanden i en serie tester), kan du spela en diskret slumpvariabel X med distributionslagen X 1 2 … P, efter att ha gjort detta på samma sätt som i punkt 1. Samtidigt tror vi att

r r 1 R 2 … r sid

Om X tar på sig värdet x i = i, då inträffade händelsen i detta test A i.

4. Spela en kontinuerlig slumpvariabel.

a) Metod för inversa funktioner.

Anta att vi vill spela en kontinuerlig slumpvariabel X, det vill säga få en sekvens av dess möjliga värden x i (i = 1, 2, …, n), att känna till distributionsfunktionen F(x).

Sats 24.2. Om r iär ett slumptal, sedan det möjliga värdet x i spelas kontinuerlig slumpmässig variabel X med en given fördelningsfunktion F(x), motsvarande r i, är roten till ekvationen

F(x i) = r i. (24.1)

Bevis.

Därför att F(x) ökar monotont i intervallet från 0 till 1, då finns det ett (och unikt) värde på argumentet x i, där fördelningsfunktionen tar värdet r i. Detta betyder att ekvation (24.1) har en unik lösning: x i= F -1 (r i), Var F-1 - funktion inverterad till F. Låt oss bevisa att roten till ekvationen (24.1) är ett möjligt värde på den slumpvariabel som övervägs X. Låt oss först anta det x iär det möjliga värdet av någon slumpvariabel x, och vi bevisar att sannolikheten för att x faller in i intervallet ( s, d) är jämställd F(d) – F(c). Ja, på grund av monotoni F(x) och det F(x i) = r i. Sedan

Därför är sannolikheten att x faller in i intervallet ( CD) är lika med ökningen av fördelningsfunktionen F(x) på detta intervall är därför x = X.

Spela 3 möjliga värden av en kontinuerlig slumpvariabel X, jämnt fördelat i intervallet (5; 8).

F(x) = , det vill säga det är nödvändigt att lösa ekvationen. Låt oss välja 3 slumptal: 0,23; 0,09 och 0,56 och ersätt dem i denna ekvation. Låt oss få motsvarande möjliga värden X:

b) Superpositionsmetod.

Om fördelningsfunktionen för den slumpmässiga variabeln som spelas kan representeras som en linjär kombination av två fördelningsfunktioner:

sedan, sedan när X®¥ F(x) ® 1.

Låt oss introducera en extra diskret slumpvariabel Z med distributionslagen

Z 12 . Låt oss välja 2 oberoende slumptal r 1 och r 2 och spela det möjliga

pC 1 C 2

menande Z efter nummer r 1 (se punkt 1). Om Z= 1, så letar vi efter det önskade möjliga värdet X från ekvationen, och om Z= 2, då löser vi ekvationen .

Det kan bevisas att i detta fall är fördelningsfunktionen för den slumpvariabel som spelas lika med den givna fördelningsfunktionen.

c) Ungefärligt spel för en normal stokastisk variabel.

Sedan för R, likformigt fördelat i (0, 1), sedan för summan P oberoende, enhetligt fördelade stokastiska variabler i intervallet (0,1). Sedan, i kraft av den centrala gränssatsen, den normaliserade slumpvariabeln vid P® ¥ kommer att ha en fördelning nära normal, med parametrarna A= 0 och s = 1. I synnerhet erhålls en ganska bra approximation när P = 12:

Så för att spela ut det möjliga värdet av den normaliserade normala slumpvariabeln X, måste du lägga till 12 oberoende slumptal och subtrahera 6 från summan.

Invers funktionsmetod

Anta att vi vill spela en kontinuerlig slumpvariabel X, dvs få en sekvens av dess möjliga värden x i (i= 1,2, ...), känna till distributionsfunktionen F(X).

Sats. Om r i ,-slumptal, sedan möjligt värdex i spelas kontinuerlig slumpvariabel X med en given fördelningsfunktionF(X), motsvarander i , är roten till ekvationen

F(X i)= r i . (»)

Bevis. Låt ett slumpmässigt tal väljas r i (0≤r i <1). Так как в интервале всех возможных зна­чений X distributionsfunktion F(X) monotont ökar från 0 till 1, då finns det i detta intervall, och bara ett, sådant värde på argumentet X i , där fördelningsfunktionen tar värdet r i. Med andra ord, ekvation (*) har en unik lösning

X i = F - 1 (r i),

Var F - 1 - invers funktion y=F(X).

Låt oss nu bevisa att roten X i ekvation (*) är det möjliga värdet för en sådan kontinuerlig slumpvariabel (vi kommer tillfälligt att beteckna den med ξ , och då ska vi se till det ξ=Х). För detta ändamål bevisar vi att sannolikheten för att träffa ξ i ett intervall, till exempel ( Med,d), tillhör intervallet för alla möjliga värden X, lika med ökningen av fördelningsfunktionen F(X) på detta intervall:

R(Med< ξ < d)= F(d)- F(Med).

Faktiskt sedan F(X)- monotont ökande funktion i intervallet av alla möjliga värden X, sedan i detta intervall motsvarar stora värden av argumentet stora värden för funktionen, och vice versa. Därför, om Med <X i < d, Den där F(c)< r i < F(d), och vice versa [det beaktas att på grund av (*) F(X i)=r i ].

Av dessa ojämlikheter följer att om en stokastisk variabel ξ som ingår i intervallet

Med< ξ < d, ξ (**)

sedan den slumpmässiga variabeln R som ingår i intervallet

F(Med)< R< F(d), (***)

och tillbaka. Således är ojämlikheter (**) och (***) ekvivalenta och därför lika sannolika:

R(Med< ξ< d)=P[F(Med)< R< F(d)]. (****)

Eftersom värdet R fördelas jämnt i intervallet (0,1), då är sannolikheten att träffa R i något intervall som hör till intervallet (0,1) är lika med dess längd (se kapitel XI, § 6, anmärkning). Särskilt,

R[F(Med)< R< F(d) ] = F(d) - F(Med).

Därför kan relationen (****) skrivas i formen

R(Med< ξ< d)= F(d) - F(Med).

Så, sannolikheten att träffa ξ i intervallet ( Med,d) är lika med ökningen av fördelningsfunktionen F(X) på detta intervall, vilket betyder att ξ=X. Med andra ord siffrorna X i, definierade av formeln (*), är de möjliga värdena för kvantiteten X s given fördelningsfunktion F(X), Q.E.D.

Regel 1.X i , kontinuerlig slumpvariabel X, känna till dess distributionsfunktion F(X), du måste välja ett slumpmässigt tal r i likställa dess fördelningsfunktioner och lösa för X i , den resulterande ekvationen

F(X i)= r i .

Anmärkning 1. Om det inte är möjligt att lösa denna ekvation explicit, använd grafiska eller numeriska metoder.

Exempel I. Spela 3 möjliga värden av en kontinuerlig slumpvariabel X, fördelade jämnt i intervallet (2, 10).

Lösning. Låt oss skriva fördelningsfunktionen för kvantiteten X, jämnt fördelat i intervallet ( A,b) (se kapitel XI, § 3, exempel):

F(X)= (Ha)/ (b-A).

Enligt villkor, a = 2, b=10, därför,

F(X)= (X- 2)/ 8.

Med hjälp av regeln i detta stycke kommer vi att skriva en ekvation för att hitta möjliga värden X i , för vilket vi likställer fördelningsfunktionen med ett slumptal:

(X i -2 )/8= r i .

Härifrån X i =8 r i + 2.

Låt oss välja tre slumpmässiga tal, till exempel, r i =0,11, r i =0,17, r i=0,66. Låt oss ersätta dessa siffror i ekvationen löst med avseende på X i , Som ett resultat får vi motsvarande möjliga värden X: X 1 =8·0,11+2==2,88; X 2 =1.36; X 3 = 7,28.

Exempel 2. Kontinuerlig slumpvariabel X fördelad enligt den exponentiallag som specificeras av fördelningsfunktionen (parametern λ > 0 är känd)

F(X)= 1 - e - λ X (x>0).

Vi måste hitta en explicit formel för att spela ut de möjliga värdena X.

Lösning. Med hjälp av regeln i detta stycke skriver vi ekvationen

1 - e - λ X i

Låt oss lösa denna ekvation för X i :

e - λ X i = 1 - r i, eller - λ X i = ln(1 - r i).

X i =1 sid(1– r i)/λ .

Slumpmässigt nummer r i innesluten i intervallet (0,1); därför är siffran 1 r i, är också slumpmässigt och tillhör intervallet (0,1). Med andra ord kvantiteterna R och 1 - R jämnt fördelade. Därför att hitta X i Du kan använda en enklare formel:

x i =- ln r i /λ.

Anmärkning 2. Det är känt att (se kapitel XI, §3)

Särskilt,

Det följer att om sannolikhetstätheten är känd f(x), sedan för att spela X det är möjligt istället för ekvationer F(x i)=r i besluta angående x i ekvationen

Regel 2. För att hitta ett möjligt värde X i (kontinuerlig slumpvariabel X, att känna till dess sannolikhetstäthet f(x) måste du välja ett slumpmässigt tal r i och besluta om X i , ekvationen

eller ekvation

Var A- minsta möjliga slutliga värde X.

Exempel 3. Sannolikhetstätheten för en kontinuerlig stokastisk variabel anges Xf(X)=λ (1-λx/2) i intervallet (0; 2/λ); utanför detta intervall f(X)= 0. Vi måste hitta en explicit formel för att spela ut de möjliga värdena X.

Lösning. I enlighet med regel 2, låt oss skriva ekvationen

Efter att ha utfört integrationen och löst den resulterande andragradsekvationen för X i, får vi äntligen

Låt oss först komma ihåg att om en slumpvariabel R fördelas enhetligt i intervallet (0,1), då är dess matematiska förväntan respektive varians lika (se kapitel XII, § 1, anmärkning 3):

M(R)= 1/2, (*)

D(R)= 1/2. (**)

Låt oss göra en summa P oberoende slumpvariabler fördelade jämnt i intervallet (0,1) Rj(j=1, 2, ...,n):

För att normalisera denna summa hittar vi först dess matematiska förväntan och varians.

Det är känt att den matematiska förväntan på summan av slumpvariabler är lika med summan av termernas matematiska förväntningar. Belopp (***) innehåller P termer, vars matematiska förväntan på grund av (*) är lika med 1/2; därför den matematiska förväntan av summan ( *** )

Det är känt att variansen av summan av oberoende slumpvariabler är lika med summan av termernas varianser. Belopp (***) innehåller n oberoende termer, vars spridning, i kraft av (**), är lika med 1/12; därav variansen av summan (***)

Därav standardavvikelsen för summan (***)

Låt oss normalisera beloppet i fråga, för vilket vi subtraherar den matematiska förväntan och dividerar resultatet med standardavvikelsen:

I kraft av den centrala gränssatsen vid p→∞ fördelningen av denna normaliserade slumpvariabel tenderar att vara normal med parametrarna a= 0 och σ=1. Vid final P fördelningen är ungefär normal. I synnerhet när P= 12 får vi en ganska bra och bekväm approximation för beräkningar

Regel. För att spela ut det möjliga värdet x i normal slumpvariabel X med parametrarna a=0 och σ=1 måste du lägga till 12 oberoende slumptal och subtrahera 6 från den resulterande summan:

Exempel, a) Spela 100 möjliga värden av normalvärdet X med parametrarna a=0 och σ=1; b) uppskatta parametrarna för det spelade värdet.

Lösning. a) Låt oss välja 12 slumpmässiga tal från den första raden i tabellen *), addera dem och subtrahera 6 från den resulterande summan; i slutändan har vi

x i=(0,10+0,09+...+0,67) - 6= - 0,99.

På samma sätt, genom att välja de första 12 siffrorna från varje nästa rad i tabellen, hittar vi de återstående möjliga värdena X.

b) Efter att ha utfört beräkningarna får vi de nödvändiga uppskattningarna:

Tillfredsställande betyg: A* nära noll, σ* skiljer sig lite från enhet.

Kommentar. Om du vill spela ett möjligt värde z i, normal slumpvariabel Z med matematiska förväntningar A och standardavvikelse σ , sedan, efter att ha spelat enligt regeln i detta stycke det möjliga värdet xi, hitta önskat möjliga värde med formeln

z i = σx i +a.

Denna formel erhålls från relationen ( z i -a)/σ=x i.

Uppgifter

1. Spela 6 värden av en diskret slumpmässig variabel X, vars distributionslag ges i form av en tabell

Notera. För att vara säker, antag att slumptal valdes: 0,73; 0,75; 0,54; 0,08; 0,28; 0,53. Rep. 10; 10; 10; 2; 3; 22; 10.

2. Spela 4 försök, var och en med en sannolikhet att en händelse inträffar A lika med 0,52.

Notera. För att vara säker, antag att slumptal valdes: 0;28; 0,53; 0,91; 0,89.

Rep. A, , .

3. Sannolikheterna för tre händelser som bildar en komplett grupp ges: R(A 1)=0,20, R(A 2)=0,32, R(A 3)= 0,48. Spela 6 utmaningar, i var och en av de givna händelserna.

Notera. För att vara säker, antag att slumptal valdes: 0,77; 0,19; 0,21; 0,51; 0,99; 0,33.

Rep. A 3,A 1 ,A 2 ,A 2 ,A 3,A 2 .

4. Händelser A och B självständig och samarbetsvillig. Spela 5 utmaningar, var och en med en sannolikhet att en händelse inträffar Aär lika med 0,5 och händelser I- 0,8.

A 1 =AB, för säkerhet, ta slumpmässiga tal: 0,34; 0,41; 0,48; 0,21; 0,57.

Rep. A 1 ,A 2 ,A 2 ,A 1 ,A 3.

5. Händelser A, B, C självständig och samarbetsvillig. Spela 4 test i vart och ett av vilka sannolikheten för att händelser ska inträffa ges: R(A)= 0,4, R(I)= 0,6, R(MED)= 0,5.

Notera. Komponera en komplett grupp av händelser: för säkerhet, anta att slumpmässiga tal är valda: 0,075; 0,907; 0,401; 0,344.

Svar A 1 ,En 8,A 4,A 4.

6. Händelser A Och I beroende och samarbetsvillig. Spela 4 test, som vart och ett har gett sannolikheter: R(A)=0,7, R(I)=0,6, R(AB)=0,4.

Notera. Skapa en komplett grupp av händelser: A 1 =AB, för säkerhet, ta slumpmässiga tal: 0,28; 0,53; 0,91; 0,89.

Rep. A 1 , A 2 , A 4 , A 3 .

7. Spela 3 möjliga värden av en kontinuerlig slumpvariabel X, som fördelas enligt exponentiallagen och specificeras av fördelningsfunktionen F(X)= 1 - e -10 x .

Notera. För tydlighetens skull, antag att slumptal valdes: 0,67; 0,79; 0,91.

Rep. 0,04; 0,02; 0,009.

8. Spela 4 möjliga värden av en kontinuerlig slumpmässig variabel X, fördelade jämnt i intervallet (6,14).

Notera. För tydlighetens skull, antag att slumpmässiga tal valdes: 0,11: 0,04; 0,61; 0,93.

Rep. 6,88; 6,32; 10,88; 13,44.

9. Hitta explicita formler för att spela en kontinuerlig slumpvariabel med superpositionsmetoden X, given fördelningsfunktion

F(x)=1- (1/3)(2е- 2 x +е -3 x:), 0<X<∞.

Rep. x= - (1/2)1п r 2 om r 1 < 2/3; X= - (1/3)1п r 2 om r 1 ≥2/3.

10. Hitta en explicit formel för att spela en kontinuerlig slumpvariabel X, given sannolikhetstäthet f(X)=b/(1 +yxa) 2 i intervallet 0≤ x≤1/(b-a); utanför detta intervall f(x)=0.

Rep. x i= - r i/(b - ar i).

11. Spela 2 möjliga värden av en normal slumpvariabel med parametrarna: a) A=0, σ =1; b) A =2, σ =3.

Notera. För säkerhet, acceptera slumptal (antal hundradelar anges nedan; till exempel motsvarar siffran 74 ett slumptal r 1 =0,74): 74. 10, 88, 82. 22, 88, 57, 07, 40, 15, 25, 70; 62, 88, 08, 78, 73, 95, 16, 05, 92, 21, 22, 30.

Rep. A) x 1 = - 0,22, x 2 = - 0.10; 6) z 1 =1,34, z 2 =2,70.

Kapitel tjugotvå

Låt det krävas att man spelar en kontinuerlig slumpvariabel X, dvs. erhålla en sekvens av dess möjliga värden (i=1, 2, ..., n), genom att känna till fördelningsfunktionen F(x).

Sats. Om är ett slumptal, då är det möjliga värdet av den spelade kontinuerliga slumpvariabeln X med en given fördelningsfunktion F (x), motsvarande , roten av ekvationen.

Regel 1. För att hitta det möjliga värdet, en kontinuerlig slumpvariabel X, som känner till dess fördelningsfunktion F (x), är det nödvändigt att välja ett slumptal, likställa dess fördelningsfunktion och lösa den resulterande ekvationen .

Anteckning 1. Om det inte är möjligt att lösa denna ekvation explicit, tillgrip då grafiska eller numeriska metoder.

Exempel 1. Spela 3 möjliga värden av en kontinuerlig slumpvariabel X, fördelade jämnt i intervallet (2, 10).

Lösning: Låt oss skriva fördelningsfunktionen för värdet X, fördelat enhetligt i intervallet (a, b): .

Enligt villkoret är därför a=2, b=10, .

Med hjälp av regel 1 kommer vi att skriva en ekvation för att hitta möjliga värden, för vilken vi likställer fördelningsfunktionen med ett slumptal:

Härifrån .

Låt oss välja tre slumpmässiga tal, till exempel, . Låt oss ersätta dessa siffror i ekvationen löst med avseende på ; Som ett resultat får vi motsvarande möjliga värden på X: ; ; .

Exempel 2. En kontinuerlig stokastisk variabel X fördelas enligt en exponentiell lag specificerad av fördelningsfunktionen (parametern är känd) (x > 0). Vi måste hitta en explicit formel för att spela ut de möjliga värdena för X.

Lösning: Med hjälp av regeln skriver vi ekvationen.

Låt oss lösa denna ekvation för: , eller .

Slumptalet finns i intervallet (0, 1); därför är talet också slumpmässigt och tillhör intervallet (0,1). Med andra ord är värdena för R och 1-R lika fördelade. Därför, för att hitta det, kan du använda en enklare formel.

Anteckning 2. Det är känt att .

Särskilt, .

Det följer att om sannolikhetstätheten är känd kan man lösa ekvationen för att spela X istället för ekvationer.

Regel 2. För att hitta det möjliga värdet av en kontinuerlig slumpvariabel X, med kunskap om dess sannolikhetstäthet, är det nödvändigt att välja ett slumptal och lösa ekvationen eller ekvationen för det där a är det minsta slutgiltiga värdet av X.

Exempel 3. Sannolikhetstätheten för en kontinuerlig stokastisk variabel X i intervallet anges; utanför detta intervall. Vi måste hitta en explicit formel för att spela ut de möjliga värdena för X.

Lösning: Låt oss skriva ekvationen i enlighet med regel 2.

Efter att ha utfört integrationen och löst den resulterande andragradsekvationen för , vi ska äntligen få det.

18.7 Ungefärligt spel för en normal slumpvariabel

Låt oss först komma ihåg att om en stokastisk variabel R är jämnt fördelad i intervallet (0, 1), så är dess matematiska förväntan respektive varians lika: M(R)=1/2, D(R)=1/12.

Låt oss sammanställa summan av n oberoende, enhetligt fördelade stokastiska variabler i intervallet (0, 1): .

För att normalisera denna summa hittar vi först dess matematiska förväntan och varians.

Det är känt att den matematiska förväntan av summan av slumpvariabler är lika med summan av termernas matematiska förväntningar. Summan innehåller n termer, vars matematiska förväntan, på grund av M(R) = 1/2, är lika med 1/2; därför den matematiska förväntan av summan

Det är känt att variansen av summan av oberoende slumpvariabler är lika med summan av termernas varianser. Summan innehåller n oberoende termer, vars varians, på grund av D(R) = 1/12, är lika med 1/12; därför summans varians

Därav standardavvikelsen för summan

Låt oss normalisera beloppet i fråga, för vilket vi subtraherar den matematiska förväntan och dividerar resultatet med standardavvikelsen: .

I kraft av den centrala gränssatsen tenderar fördelningen av denna normaliserade slumpvariabel att vara normal med parametrarna a = 0 och . För ändligt n är fördelningen ungefär normal. I synnerhet för n=12 får vi en ganska bra och bekväm approximation för beräkningar.

Uppskattningarna är tillfredsställande: nära noll, lite annorlunda än ett.

Lista över använda källor

1. Gmurman V.E. Sannolikhetsteori och matematisk statistik. – M.: Högre skola, 2001.

2. Kalinina V.N., Pankin V.F. Matematik statistik. – M.: Högre skola, 2001.

3. Gmurman V.E. En guide till att lösa problem inom sannolikhetsteori och matematisk statistik. – M.: Högre skola, 2001.

4. Kochetkov E.S., Smerchinskaya S.O., Sokolov V.V. Sannolikhetsteori och matematisk statistik. – M.:FORUM:INFRA-M, 2003.

5. Agapov G.I. Problembok om sannolikhetsteori. – M.: Högre skola, 1994.

6. Kolemaev V.A., Kalinina V.N. Sannolikhetsteori och matematisk statistik. – M.: INFRA-M, 2001.

7. Ventzel E.S. Sannolikhetsteori. – M.: Högre skola, 2001.

Skicka ditt goda arbete i kunskapsbasen är enkelt. Använd formuläret nedan

Studenter, doktorander, unga forskare som använder kunskapsbasen i sina studier och arbete kommer att vara er mycket tacksamma.

Postat på http://www.allbest.ru/

LEKTION 1

Simulering av slumpmässiga händelser med en given distributionslag

Spela en diskret slumpmässig variabel

Låt det vara nödvändigt att spela en diskret slumpvariabel, dvs. erhåll en sekvens av dess möjliga värden x i (i = 1,2,3,...n), med kunskap om distributionslagen för X:

Låt oss beteckna med R en kontinuerlig stokastisk variabel. Värdet på R är jämnt fördelat i intervallet (0,1). Med r j (j = 1,2,...) betecknar vi de möjliga värdena för den slumpmässiga variabeln R. Låt oss dividera intervallet 0< R < 1 на оси 0r точками с координатами на n частичных интервалов.

Då får vi:

Det kan ses att längden på delintervallet med index i är lika med sannolikheten P med samma index. Längd

Sålunda, när ett slumptal r i faller in i intervallet, antar slumpvariabeln X värdet x i med sannolikhet Pi.

Det finns följande teorem:

Om varje slumptal som faller in i intervallet är associerat med ett möjligt värde x i, kommer värdet som spelas att ha en given distributionslag

Algoritm för att spela en diskret slumpvariabel specificerad av distributionslagen

1. Det är nödvändigt att dela upp intervallet (0,1) för 0r-axeln i n delintervall:

2. Välj (till exempel från en tabell med slumptal eller på en dator) ett slumptal r j .

Om r j föll in i intervallet, fick den diskreta slumpvariabeln som spelas ett möjligt värde x i .

Spela en kontinuerlig slumpmässig variabel

Låt det vara nödvändigt att spela en kontinuerlig slumpvariabel X, dvs. få en sekvens av dess möjliga värden x i (i = 1,2,...). I detta fall är fördelningsfunktionen F(X) känd.

Existerar Nästa sats.

Om r i är ett slumptal, så är det möjliga värdet x i för den spelade kontinuerliga slumpvariabeln X med en känd fördelningsfunktion F(X) som motsvarar r i roten till ekvationen

Algoritm för att spela en kontinuerlig slumpvariabel:

1. Du måste välja ett slumptal r i .

2. Jämställ det valda slumptalet med den kända fördelningsfunktionen F(X) och få en ekvation.

3. Lös denna ekvation för x i. Det resulterande värdet x i kommer samtidigt att motsvara slumptalet r i . och den givna distributionslagen F(X).

Exempel. Spela 3 möjliga värden av en kontinuerlig slumpvariabel X, fördelade jämnt i intervallet (2; 10).

Fördelningsfunktionen för X-värdet har följande form:

Som villkor är a = 2, b = 10, därför

I enlighet med algoritmen för att spela en kontinuerlig slumpmässig variabel, likställer vi F(X) till det valda slumptalet r i .. Vi får härifrån:

Ersätt dessa siffror i ekvation (5.3) Vi får motsvarande möjliga värden på x:

Problem med att modellera slumpmässiga händelser med en given distributionslag

1. Det krävs att man spelar 10 värden av en diskret slumpvariabel, dvs. erhålla en sekvens av dess möjliga värden x i (i=1,2,3,...n), med kunskap om distributionslagen X

Låt oss välja ett slumptal r j från tabellen med slumptal: 0,10; 0,12; 0,37; 0,09; 0,65; 0,66; 0,99; 0,19; 0,88; 0,59; 0,78

2. Frekvensen för mottagande av förfrågningar om tjänst är föremål för den exponentiella distributionslagen (), x, parametern l är känd (hädanefter l = 1/t - intensiteten av mottagandet av förfrågningar)

l=0,5 förfrågningar/timme. Bestäm sekvensen av värden för varaktigheten av intervallen mellan mottaganden av ansökningar. Antalet implementeringar är 5. Antal r j: 0,10; 0,12; 0,37; 0,09; 0,65; 0,99;

LEKTION 2

Kösystem

System där det å ena sidan finns massiva förfrågningar om utförandet av någon typ av tjänst, och å andra sidan dessa förfrågningar tillgodoses, kallas kösystem. Varje QS tjänar till att uppfylla flödet av förfrågningar.

QS inkluderar: kravkälla, inkommande flöde, kö, serveringsenhet, utgående flöde av förfrågningar.

SMO är indelade i:

QS med förluster (misslyckanden)

Kö med väntan (obegränsad kölängd)

QS med begränsad kölängd

QS med begränsad väntetid.

Baserat på antalet kanaler eller tjänsteenheter kan QS-system vara enkanaliga eller flerkanaliga.

Efter lokalisering av kravkällan: öppen och stängd.

Efter antal serviceelement per krav: enfas och flerfas.

En av klassificeringsformerna är D. Kendall-klassificeringen - A/B/X/Y/Z

A - bestämmer tidsfördelningen mellan ankomster;

B - bestämmer fördelningen av tjänstetiden;

X - bestämmer antalet tjänstekanaler;

Y - bestämmer systemkapaciteten (kölängd);

Z - bestämmer tjänstens ordning.

När systemkapaciteten är oändlig och servicekön följer först till kvarn-principen, utelämnas Y/Z-delarna. Den första siffran (A) använder följande symboler:

M-fördelningen har en exponentiell lag,

G - frånvaron av några antaganden om serviceprocessen, eller den är identifierad med symbolen GI, vilket betyder en återkommande serviceprocess,

D-deterministisk (fast servicetid),

E n - Erlang nth order,

NM n - hyper-Erlang n:e ordningen.

Den andra siffran (B) använder samma symboler.

Den fjärde siffran (Y) visar buffertkapaciteten, d.v.s. maximalt antal platser i kön.

Den femte siffran (Z) anger metoden för val från kön i ett väntesystem: SP-lik sannolikhet, FF-först in-först ut, LF-sist in-först ut, PR-prioritet.

För uppgifter:

l är det genomsnittliga antalet inkomna ansökningar per tidsenhet

µ - genomsnittligt antal ansökningar per tidsenhet

Kanal 1 belastningsfaktor, eller procentandelen av tid som kanalen är upptagen.

Huvuddragen:

1) Avvisa - sannolikhet för fel - sannolikheten att systemet vägrar service och kravet går förlorat. Detta händer när kanalen eller alla kanaler är upptagna (TFoP).

För en flerkanalig QS P öppen =P n, där n är antalet tjänstekanaler.

För en QS med begränsad kölängd P öppen =P n + l, där l är den tillåtna kölängden.

2) Relativ q och absolut A-systemkapacitet

q= 1-P öppen A=ql

3) Totalt antal krav i systemet

L sys = n - för SMO med misslyckanden, n är antalet kanaler som upptas av service.

För QS med väntetid och begränsad kölängd

L sys = n+L cool

där L cool är det genomsnittliga antalet förfrågningar som väntar på att tjänsten ska börja osv.

Vi kommer att överväga de återstående egenskaperna när vi löser problemen.

Enkanaliga och flerkanaliga kösystem. System med fel.

Den enklaste enkanalsmodellen med ett probabilistiskt ingångsflöde och serviceprocedur är en modell som kännetecknas av en exponentiell fördelning av både varaktigheterna av intervallen mellan mottaganden av krav och servicevaraktigheterna. I det här fallet har distributionstätheten för varaktigheten av intervall mellan mottaganden av förfrågningar formen

Täthet av distribution av tjänstelängder:

Flödena av förfrågningar och tjänster är enkla. Låt systemet arbeta med fel. Denna typ av QS kan användas vid modellering av överföringskanaler i lokala nätverk. Det är nödvändigt att bestämma den absoluta och relativa genomströmningen av systemet. Låt oss föreställa oss detta kösystem i form av en graf (Figur 2), som har två tillstånd:

S 0 - kanalfri (väntar);

S 1 - kanal är upptagen (förfrågan betjänas).

Figur 2. Tillståndsdiagram för en enkanalig QS med fel

Låt oss beteckna tillståndssannolikheterna: P 0 (t) - sannolikheten för det "kanalfria" tillståndet; P 1 (t) - sannolikheten för tillståndet "kanalen upptagen". Med hjälp av den märkta tillståndsgrafen sammanställer vi ett system av Kolmogorovs differentialekvationer för tillståndssannolikheter:

Systemet med linjära differentialekvationer har en lösning som tar hänsyn till normaliseringsvillkoret P 0 (t) + P 1 (t) = 1. Lösningen för detta system kallas ostadig, eftersom den direkt beror på t och ser ut så här:

P 1 (t) = 1 - P 0 (t) (3.4.3)

Det är lätt att verifiera att för en enkanalig QS med fel är sannolikheten P 0 (t) inget annat än den relativa kapaciteten hos systemet q. Po är sannolikheten att kanalen vid tidpunkten t är ledig och en begäran som anländer vid tidpunkten t kommer att betjänas, och därför, för en given tid t, det genomsnittliga förhållandet mellan antalet förfrågningar som betjänas och antalet mottagna. är också lika med Po (t), dvs. q = Po (t).

Efter ett stort tidsintervall (vid) uppnås ett stationärt (stabilt) läge:

Genom att känna till den relativa genomströmningen är det lätt att hitta den absoluta. Absolut genomströmning (A) är det genomsnittliga antalet förfrågningar som ett kösystem kan betjäna per tidsenhet:

Sannolikheten för att vägra att betjäna en begäran kommer att vara lika med sannolikheten för "kanalen upptagen":

Detta värde på P öppen kan tolkas som den genomsnittliga andelen ej inlämnade ansökningar bland de inlämnade.

I de allra flesta fall, i praktiken, är kösystem flerkanaliga, och därför är modeller med n betjäningskanaler (där n>1) av otvivelaktigt intresse. Köprocessen som beskrivs av denna modell kännetecknas av intensiteten av ingångsflödet l, medan inte fler än n klienter (applikationer) kan betjänas parallellt. Den genomsnittliga varaktigheten för service av en begäran är 1/m. In- och utströmmarna är Poisson. Driftssättet för en speciell servicekanal påverkar inte driftsättet för andra servicekanaler i systemet, och varaktigheten av serviceproceduren för varje kanal är en slumpmässig variabel som är föremål för en exponentiell distributionslag. Det slutliga målet med att använda n parallellkopplade tjänstekanaler är att öka (jämfört med ett enkanalssystem) hastigheten på serviceförfrågningar genom att betjäna n klienter samtidigt. Tillståndsdiagrammet för ett flerkanaligt kösystem med fel har den form som visas i figur 4.

Figur 4. Tillståndsdiagram för en flerkanalig QS med fel

S 0 - alla kanaler är gratis;

S 1 - en kanal är upptagen, resten är gratis;

S k - exakt k kanaler är upptagna, resten är gratis;

S n - alla n kanaler är upptagna, resten är gratis.

Kolmogorovs ekvationer för sannolikheterna för systemtillstånd P 0 , ... , P k , ... P n kommer att ha följande form:

De initiala förutsättningarna för att lösa systemet är:

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0.

Systemets stationära lösning har formen:

Formler för beräkning av sannolikheter P k (3.5.1) kallas Erlang-formler.

Låt oss bestämma de probabilistiska egenskaperna för funktionen hos en flerkanalig QS med fel i ett stationärt läge:

1) sannolikhet för misslyckande:

eftersom en begäran avvisas om den kommer vid en tidpunkt då alla n kanalerna är upptagna. Värdet P öppen kännetecknar fullständigheten av att serva det inkommande flödet;

2) sannolikheten att begäran kommer att accepteras för service (det är också den relativa kapaciteten hos systemet q) kompletterar P öppen till en:

3) absolut genomströmning

4) det genomsnittliga antalet kanaler upptagna av tjänsten () är som följer:

Värdet kännetecknar graden av belastning av QS.

Uppgiftertill lektion 2

1. En kommunikationsgren med en kanal tar emot det enklaste flödet av meddelanden med en intensitet på l = 0,08 meddelanden per sekund. Sändningstiden fördelas enligt exp-lagen. Betjäning av ett meddelande sker med intensitet µ=0,1. Meddelanden som anländer vid tidpunkter när den betjänande kanalen är upptagen med att sända ett tidigare mottaget meddelande får ett överföringsfel.

Coeff. Relativ kanalbelastning (sannolikhet för kanalbeläggning)

P avvisa sannolikheten för misslyckande att ta emot ett meddelande

Q relativ kapacitet för internodgrenen

Och kommunikationsgrenens absoluta genomströmning.

2. Kommunikationsgrenen har en kanal och tar emot meddelanden var 10:e sekund. Servicetiden för ett meddelande är 5 sekunder. Meddelandets sändningstiden är fördelad enligt en exponentiell lag. Meddelanden som kommer när kanalen är upptagen nekas service.

Definiera

Rzan - sannolikhet för beläggning av kommunikationskanaler (relativ belastningsfaktor)

Q - relativ genomströmning

A - absolut kapacitet för kommunikationsgrenen

4. Den internodala grenen av det sekundära kommunikationsnätverket har n = 4 kanaler. Flödet av meddelanden som anländer för överföring genom kommunikationsgrenkanalerna har en intensitet = 8 meddelanden per sekund. Den genomsnittliga sändningstiden för ett meddelande är t = 0,1 sekunder. Ett meddelande som anländer vid en tidpunkt då alla n kanalerna är upptagna tar emot ett överföringsfel längs kommunikationsgrenen. Hitta egenskaperna hos SMO:

LEKTION 3

Enkanalssystem med standby

Låt oss nu överväga en enkanalig QS med väntan. Kösystemet har en kanal. Det inkommande flödet av serviceförfrågningar är det enklaste flödet med intensitet. Intensiteten hos tjänsteflödet är lika (dvs i genomsnitt kommer en kontinuerligt upptagen kanal att utfärda betjänade förfrågningar). Varaktigheten av tjänsten är en slumpmässig variabel som omfattas av lagen om exponentiell distribution. Serviceflödet är det enklaste Poisson-flödet av händelser. En begäran som tas emot när kanalen är upptagen står i kö och väntar på service. Denna QS är den vanligaste inom modellering. Med en eller annan grad av approximation kan den användas för att simulera nästan vilken nod som helst i ett lokalt datornätverk (LAN).

Låt oss anta att oavsett hur många förfrågningar som kommer till serveringssystemets ingång, detta system (kö + klienter som betjänas) kan inte tillgodose fler än N-krav (ansökningar), d.v.s. kunder som inte är parkerade tvingas betjänas någon annanstans. System M/M/1/N. Slutligen har källgenererande tjänsteförfrågningar obegränsad (oändligt stor) kapacitet. Tillståndsdiagrammet för QS har i detta fall den form som visas i figur 3

Figur 3. Tillståndsdiagram för en enkanalig QS med väntan (schema för död och reproduktion)

QS-staterna har följande tolkning:

S 0 - "kanalfri";

S 1 - "kanal upptagen" (ingen kö);

S 2 - "kanal upptagen" (en begäran är i kö);

S n - "kanal upptagen" (n -1 applikationer är i kö);

S N - "kanal upptagen" (N - 1 applikationer står i kö).

Den stationära processen i detta system kommer att beskrivas av följande system av algebraiska ekvationer:

där p=lastfaktor

n - tillståndsnummer.

Lösningen på ovanstående ekvationssystem för vår QS-modell har formen:

Initialt sannolikhetsvärde för en QS med begränsad kölängd

För en QS med en oändlig kö Н =? :

P 0 = 1- s (3.4.7)

Det bör noteras att uppfyllandet av stationaritetsvillkoret för en given QS inte är nödvändig, eftersom antalet ansökningar som tas upp till serveringssystemet kontrolleras genom att införa en begränsning av köns längd, som inte kan överstiga (N - 1) och inte av förhållandet mellan intensiteterna för inflödet, dvs inte förhållandet c = l/m.

Till skillnad från enkanalssystemet, som ansågs ovan och med en obegränsad kö, existerar i detta fall en stationär fördelning av antalet förfrågningar för eventuella ändliga värden på lastfaktorn c.

Låt oss bestämma egenskaperna hos en enkanals QS med väntan och en begränsad kölängd lika med (N - 1) (M/M/1/N), såväl som för en enkanals QS med en buffert med obegränsad kapacitet (M/M/1/?). För en QS med en oändlig kö, villkoret med<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) sannolikhet för att avslå en ansökan:

En av de viktigaste egenskaperna hos system där förlust av förfrågningar är möjlig är sannolikheten P förlust för att en godtycklig begäran kommer att gå förlorad. I detta fall sammanfaller sannolikheten att förlora en godtycklig begäran med sannolikheten att vid ett godtyckligt ögonblick är alla vänteplatser upptagna, d.v.s. Följande formel är giltig: Р från k = Р Н

2) relativ systemkapacitet:

För SMO med obegränsatkön q =1, därför att alla förfrågningar kommer att betjänas

3) absolut genomströmning:

4) det genomsnittliga antalet ansökningar i systemet:

L S med obegränsad kö

5) genomsnittlig tid som en applikation stannar i systemet:

För obegränsad kö

6) genomsnittlig vistelsetid för en klient (applikation) i kön:

Med obegränsad kö

7) genomsnittligt antal ansökningar (klienter) i kön (kölängd):

med obegränsad kö

Genom att jämföra uttrycken för den genomsnittliga väntetiden i kön T och och formeln för den genomsnittliga längden på kön L och, samt den genomsnittliga uppehållstiden för förfrågningar i systemet T S och det genomsnittliga antalet förfrågningar i systemet L S, vi ser det

L och =l*T och L s =l* T s

Observera att dessa formler också är giltiga för många kösystem som är mer generella än M/M/1-systemet som övervägs och som kallas Littles formler. Den praktiska betydelsen av dessa formler är att de eliminerar behovet av att direkt beräkna värdena på T och och T s med ett känt värde på värdena L och och L s och vice versa.

Enkanaliga uppgifter SMOmed förväntan, Medväntar ochbegränsad kölängd

1. Givet en enrads QS med obegränsad kölagring. Ansökningar tas emot varje t = 14 sekunder. Den genomsnittliga sändningstiden för ett meddelande är t=10 sekunder. Meddelanden som anländer vid tidpunkter när den betjänande kanalen är upptagen tas emot i kön utan att lämna den innan servicen påbörjas.

Bestäm följande prestandaindikatorer:

2. Internodkommunikationsgrenen, som har en kanal och ett köminne för m=3 väntande meddelanden (N-1=m), tar emot det enklaste meddelandeflödet med en intensitet av l=5 meddelanden. i sekunder Tiden för meddelandeöverföring fördelas enligt en exponentiell lag. Den genomsnittliga sändningstiden för ett meddelande är 0,1 sekunder. Meddelanden som anländer vid tidpunkter när den betjänande kanalen är upptagen med att sända ett tidigare mottaget meddelande och det inte finns något ledigt utrymme i enheten avvisas.

P avvisa - sannolikheten för misslyckande att ta emot ett meddelande

L-system - det genomsnittliga totala antalet meddelanden i kön och sänds längs kommunikationsgrenen

T och - den genomsnittliga tid ett meddelande ligger kvar i kön innan överföringen börjar

T syst - den genomsnittliga totala tiden ett meddelande finns kvar i systemet, bestående av den genomsnittliga väntetiden i kön och den genomsnittliga sändningstiden

Q - relativ genomströmning

A - absolut genomströmning

3. Internodgrenen av det sekundära kommunikationsnätverket, som har en kanal och ett köminne för m = 4 (N-1=4) väntande meddelanden, tar emot det enklaste meddelandeflödet med en intensitet = 8 meddelanden per sekund. Meddelandets sändningstiden är fördelad enligt en exponentiell lag. Den genomsnittliga sändningstiden för ett meddelande är t = 0,1 sekund. Meddelanden som anländer vid tidpunkter när den betjänande kanalen är upptagen med att sända ett tidigare mottaget meddelande och det inte finns något ledigt utrymme i enheten avvisas av kön.

P öppen - sannolikheten för misslyckande att ta emot ett meddelande för överföring över kommunikationskanalen för internodgrenen;

L och - det genomsnittliga antalet meddelanden i kön till kommunikationsgrenen i köns sekundära nätverk;

L-system - det genomsnittliga totala antalet meddelanden i kön och sänds längs kommunikationsgrenen av det sekundära nätet;

T och - den genomsnittliga tid ett meddelande finns kvar i kön innan överföringen börjar;

Rzan - sannolikheten för att kommunikationskanalen är upptagen (relativ kanalbelastningskoefficient);

Q är den relativa kapaciteten för den internodala grenen;

A är den absoluta kapaciteten för den internodala grenen;

4. Internodkommunikationsgrenen, som har en kanal och ett köminne för m=2 väntande meddelanden, tar emot det enklaste meddelandeflödet med en intensitet av l=4 meddelanden. i sekunder Meddelandets överföringstid fördelas enligt en exponentiell lag. Den genomsnittliga sändningstiden för ett meddelande är 0,1 sekunder. Meddelanden som anländer vid tidpunkter när den betjänande kanalen är upptagen med att sända ett tidigare mottaget meddelande och det inte finns något ledigt utrymme i enheten avvisas.

Bestäm följande prestandaindikatorer för kommunikationsgrenen:

P avvisa - sannolikheten för misslyckande att ta emot ett meddelande

L och - genomsnittligt antal meddelanden i kön till kommunikationsgrenen

L-system - det genomsnittliga totala antalet meddelanden i kön och sänds längs kommunikationsgrenen

T och - den genomsnittliga tid ett meddelande ligger kvar i kön innan överföringen börjar

T syst - den genomsnittliga totala tiden ett meddelande finns kvar i systemet, bestående av den genomsnittliga väntetiden i kön och den genomsnittliga sändningstiden

R zan - sannolikhet för beläggning av kommunikationskanaler (relativ kanalbelastningskoefficient c)

Q - relativ genomströmning

A - absolut genomströmning

5. Internodgrenen av det sekundära kommunikationsnätverket, som har en kanal och en obegränsad volymlagringskö av väntande meddelanden, tar emot det enklaste flödet av meddelanden med en intensitet av l = 0,06 meddelanden per sekund. Den genomsnittliga sändningstiden för ett meddelande är t = 10 sekunder. Meddelanden som kommer vid tidpunkter när kommunikationskanalen är upptagen tas emot i kön och lämnar den inte förrän tjänsten börjar.

Bestäm följande prestandaindikatorer för den sekundära nätverkskommunikationsgrenen:

L och - det genomsnittliga antalet meddelanden i kön till kommunikationsgrenen;

L-system - det genomsnittliga totala antalet meddelanden i kön och överförda längs kommunikationsgrenen;

T och - den genomsnittliga tiden ett meddelande stannar i kön;

T syst är den genomsnittliga totala tiden ett meddelande finns kvar i systemet, vilket är summan av den genomsnittliga väntetiden i kön och den genomsnittliga sändningstiden;

Rzan är sannolikheten för att kommunikationskanalen är upptagen (relativ kanalbelastningsfaktor);

Q - relativ kapacitet hos den internodala grenen;

A - absolut kapacitet för den internodala grenen

6. Givet en enrads QS med obegränsad kölagring. Ansökningar tas emot var t = 13:e sekund. Genomsnittlig tid för att skicka ett meddelande

t=10 sekunder. Meddelanden som anländer vid tidpunkter när den betjänande kanalen är upptagen tas emot i kön utan att lämna den innan servicen påbörjas.

Bestäm följande prestandaindikatorer:

L och - genomsnittligt antal meddelanden i kön

L-system - det genomsnittliga totala antalet meddelanden i kön och sänds längs kommunikationsgrenen

T och - den genomsnittliga tid ett meddelande ligger kvar i kön innan överföringen börjar

T syst - den genomsnittliga totala tiden ett meddelande finns kvar i systemet, bestående av den genomsnittliga väntetiden i kön och den genomsnittliga sändningstiden

Rzan - sannolikhet för beläggning (relativ kanalbelastningskoefficient c)

Q - relativ genomströmning

A - absolut genomströmning

7. Den specialiserade diagnostiska posten är en enkanalig QS. Antalet parkeringsplatser för bilar som väntar på diagnostik är begränsat och lika med 3 [(N - 1) = 3]. Om alla parkeringsplatser är upptagna, det vill säga det redan står tre bilar i kön, kommer nästa bil som kommer för diagnos inte att ställas i kön för service. Flödet av bilar som anländer för diagnostik fördelas enligt Poissons lag och har en intensitet = 0,85 (bilar per timme). Fordonsdiagnostiden är fördelad enligt en exponentiell lag och är i genomsnitt 1,05 timmar.

Det krävs för att bestämma de probabilistiska egenskaperna hos en diagnosstation som arbetar i stationärt läge: P 0 , P 1 , P 2 , P 3 , P 4 , P open, q,A, L och, L sys, T och, T sys

LEKTION 4

Flerkanalig QS med väntan, med väntan och begränsad kölängd

Låt oss överväga ett flerkanaligt kösystem med väntan. Denna typ av QS används ofta vid modellering av grupper av LAN-abonnentterminaler som arbetar i interaktivt läge. Köprocessen kännetecknas av följande: in- och utflödena är Poisson med intensiteter respektive; Högst n klienter kan betjänas parallellt. Systemet har n servicekanaler. Den genomsnittliga varaktigheten av tjänsten för en klient är 1/m för varje kanal. Detta system hänvisar också till processen för död och reproduktion.

c=l/nm - förhållandet mellan intensiteten av det inkommande flödet och den totala intensiteten av tjänsten, är systemets belastningsfaktor

(Med<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

där Po är sannolikheten för det fria tillståndet för alla kanaler med en obegränsad kö, k är antalet förfrågningar.

om vi tar c = l / m, så kan P 0 bestämmas för en obegränsad kö:

För en begränsad kö:

där m är kölängden

Med obegränsad kö:

Relativ kapacitet q=1,

Absolut kapacitet A=l,

Genomsnittligt antal upptagna kanaler Z=A/m

Med begränsad kö

1 Internodgrenen i det sekundära kommunikationsnätverket har n = 4 kanaler. Flödet av meddelanden som anländer för överföring genom kommunikationsgrenkanalerna har en intensitet = 8 meddelanden per sekund. Medeltiden t = 0,1 för att sända ett meddelande av varje kommunikationskanal är t/n = 0,025 sekunder. Väntetiden för meddelanden i kön är obegränsad. Hitta egenskaperna hos SMO:

P öppen - sannolikhet för meddelandeöverföringsfel;

Q är den relativa kapaciteten för kommunikationsgrenen;

A är den absoluta genomströmningen av kommunikationsgrenen;

Z - genomsnittligt antal upptagna kanaler;

L och - genomsnittligt antal meddelanden i kön;

T = genomsnittlig väntetid;

T syst - den genomsnittliga totala tiden för meddelanden som stannar i kön och sänds längs kommunikationsgrenen.

2. En mekanisk verkstad av anläggningen med tre stolpar (kanaler) utför reparationer av mindre mekanisering. Flödet av felaktiga mekanismer som anländer till verkstaden är Poisson och har en intensitet = 2,5 mekanismer per dag, den genomsnittliga reparationstiden för en mekanism är fördelad enligt den exponentiella lagen och är lika med = 0,5 dagar. Låt oss anta att det inte finns någon annan verkstad på anläggningen, och därför kan kön av mekanismer framför verkstaden växa nästan obegränsat. Det är nödvändigt att beräkna följande gränsvärden för systemets probabilistiska egenskaper:

Sannolikheter för systemtillstånd;

Genomsnittligt antal ansökningar i kön för service;

Genomsnittligt antal ansökningar i systemet;

Genomsnittlig tid som en applikation står i kö;

Den genomsnittliga varaktigheten av en applikations vistelse i systemet.

3. Internodgrenen av det sekundära kommunikationsnätverket har n=3 kanaler. Flödet av meddelanden som anländer för överföring genom kommunikationsgrenkanalerna har en intensitet av 1 = 5 meddelanden per sekund. Den genomsnittliga sändningstiden för ett meddelande är t=0,1, t/n=0,033 sek. Kölagringen av meddelanden som väntar på överföring kan innehålla upp till m= 2 meddelanden. Ett meddelande som anländer vid en tidpunkt då alla platser i kön är upptagna tar emot ett överföringsfel längs kommunikationsgrenen. Hitta egenskaperna hos QS:en: P öppen - sannolikhet för meddelandeöverföringsfel, Q - relativ genomströmning, A - absolut genomströmning, Z - genomsnittligt antal upptagna kanaler, L och - genomsnittligt antal meddelanden i kön, T so - genomsnittlig väntetid tid, T-system - den genomsnittliga totala tiden ett meddelande finns kvar i kön och sänds längs kommunikationsgrenen.

LEKTION 5

Stängd QS

Låt oss överväga en maskinparksservicemodell, som är en modell av ett slutet kösystem. Hittills har vi endast övervägt kösystem för vilka intensiteten av det inkommande flödet av förfrågningar inte beror på systemets tillstånd. I det här fallet är källan till förfrågningar extern till QS och genererar ett obegränsat flöde av förfrågningar. Låt oss överväga kösystem för vilka det beror på systemets tillstånd, och kravkällan är intern och genererar ett begränsat flöde av förfrågningar. Till exempel servas en maskinpark som består av N maskiner av ett team av R-mekaniker (N > R), och varje maskin kan endast servas av en mekaniker. Här är maskiner källor till krav (förfrågningar om service), och mekaniker är servicekanaler. En defekt maskin, efter service, används för sitt avsedda syfte och blir en potentiell källa till servicekrav. Uppenbarligen beror intensiteten på hur många maskiner som för närvarande är i drift (N - k) och hur många maskiner som servas eller står i kö och väntar på service (k). I den aktuella modellen bör kravkällans kapacitet anses vara begränsad. Det inkommande kravflödet kommer från ett begränsat antal driftmaskiner (N - k), som vid slumpmässiga tillfällen går sönder och kräver underhåll. Dessutom är varje maskin från (N - k) i drift. Genererar ett Poisson-flöde av krav med intensitet X oavsett andra objekt, det totala (totala) inkommande flödet har intensitet. En begäran som kommer in i systemet när minst en kanal är ledig behandlas omedelbart. Om en begäran hittar alla kanaler upptagna med att betjäna andra förfrågningar, lämnar den inte systemet, utan hamnar i en kö och väntar tills en av kanalerna blir ledig. I ett slutet kösystem bildas alltså det inkommande kravflödet från det utgående. Systemtillståndet Sk kännetecknas av det totala antalet förfrågningar som betjänas och i kö lika med k. För det slutna systemet som betraktas är uppenbarligen k = 0, 1, 2, ... , N. Dessutom, om systemet är i tillståndet Sk, är antalet objekt i drift lika med (N - k) . Om är intensiteten i flödet av krav per maskin, då:

Systemet med algebraiska ekvationer som beskriver driften av en sluten slinga QS i stationärt läge är som följer:

När vi löser detta system finner vi sannolikheten för det k:te tillståndet:

Värdet på P 0 ​​bestäms från villkoret för att normalisera de erhållna resultaten med formlerna för P k , k = 0, 1, 2, ... , N. Låt oss bestämma följande probabilistiska egenskaper hos systemet:

Genomsnittligt antal förfrågningar i kö för tjänst:

Genomsnittligt antal förfrågningar i systemet (servering och kö)

genomsnittligt antal mekaniker (kanaler) "tomgång" på grund av arbetsbrist

Tomgångsförhållande för det betjänade objektet (maskinen) i kön

Utnyttjandegrad av anläggningar (maskiner)

Avbrottstid för servicekanaler (mekanik)

Genomsnittlig väntetid för service (väntetid för service i kö)

Stängt QS-problem

1. Låt två ingenjörer med lika produktivitet tilldelas service på tio persondatorer (PC). Flödet av fel (fel) i en dator är Poisson med intensitet = 0,2. PC-underhållstiden följer den exponentiella lagen. Den genomsnittliga tiden för service av en dator av en tekniker är: = 1,25 timmar. Följande alternativ för serviceorganisation är möjliga:

Båda ingenjörerna servar alla tio datorerna, så om en PC misslyckas servas den av en av de fria ingenjörerna, i det här fallet R = 2, N = 10;

Var och en av de två ingenjörerna har fem datorer som tilldelats honom. I detta fall R = 1, N = 5.

Det är nödvändigt att välja det bästa alternativet för att organisera PC-underhåll.

Det är nödvändigt att bestämma alla sannolikheter för tillstånd P k: P 1 - P 10, med hänsyn till att med hjälp av resultaten av beräkningen av P k beräknar vi P 0

LEKTION 6

Trafikberäkning.

Teletrafikteori är en del av köteorin. Grunden till teorin om teletrafik lades av den danske vetenskapsmannen A.K. Erlang. Hans verk publicerades 1909-1928. Låt oss ge viktiga definitioner som används i teorin om teletrafik (TT). Termen "trafik" motsvarar termen "telefonbelastning". Detta hänvisar till den belastning som skapas av flödet av samtal, krav och meddelanden som kommer till QS:ns ingångar. Trafikvolymen är mängden av det totala, integrerade tidsintervallet som missats av en eller annan resurs under vilken denna resurs var upptagen under den analyserade tidsperioden. En arbetsenhet kan betraktas som en andra sysselsättning av en resurs. Ibland kan du läsa om en timmes arbete, och ibland bara sekunder eller timmar. ITU-rekommendationer ger dock trafikvolymdimensionen i erlango-timmar. För att förstå innebörden av en sådan måttenhet måste vi överväga en annan trafikparameter - trafikintensitet. I det här fallet talar de ofta om den genomsnittliga trafikintensiteten (belastningen) på en viss given pool (uppsättning) av resurser. Om vid varje tidpunkt t från ett givet intervall (t 1,t 2) antalet resurser från en given uppsättning upptagen med servicetrafik är lika med A(t), så kommer den genomsnittliga trafikintensiteten att vara

Värdet av trafikintensitet karakteriseras som det genomsnittliga antalet resurser som upptas av trafiken vid ett givet tidsintervall. Enheten för att mäta belastningsintensitet är en Erlang (1 Erl, 1 E), dvs. 1 Erlang är en sådan trafikintensitet som kräver full sysselsättning av en resurs, eller, med andra ord, där resursen utför arbete värt en andra sysselsättning på en sekund. I amerikansk litteratur kan du ibland hitta en annan måttenhet som kallas CCS-Centrum (eller hundra) Calls Second. CCS-numret återspeglar serverns ockupationstid i 100 sekunders intervaller per timme. Den uppmätta intensiteten i CCS kan omvandlas till Erlang med formeln 36CCS=1 Erl.

Trafik som genereras av en källa och uttryckt i timmars sysselsättning är lika med produkten av antalet samtalsförsök c under ett visst tidsintervall T och den genomsnittliga varaktigheten av ett försök t: y = c t (h-z). Trafiken kan beräknas på tre olika sätt:

1) låt antalet samtal c per timme vara 1800, och den genomsnittliga längden av sessionen t = 3 minuter, sedan Y = 1800 samtal. /h. 0,05 h = 90 Earl;

2) låt varaktigheterna t i för alla n ockupationer av utgångarna från en viss bunt fastställas under tiden T, då bestäms trafiken enligt följande:

3) låta antalet samtidigt upptagna utgångar av en viss stråle övervakas med lika intervall under tiden T baserat på observationsresultaten, en stegfunktion av tiden x(t) konstrueras (figur 8).

Figur 8. Prover av samtidigt upptagna strålutgångar

Trafik under tiden T kan uppskattas som medelvärdet av x(t) under den tiden:

där n är antalet sampel av samtidigt upptagna utgångar. Värdet Y är det genomsnittliga antalet samtidigt upptagna strålutgångar under tiden T.

Trafikfluktuationer. Trafiken på sekundära telefonnät fluktuerar kraftigt över tiden. Under arbetsdagen har trafikkurvan två eller till och med tre toppar (Figur 9).

Figur 9. Trafikfluktuationer under dagen

Den timme på dygnet under vilken trafik som observerats under en lång tidsperiod är störst kallas den mest trafikerade timmen (BHH). Kunskapen om trafiken i CNN är fundamentalt viktig, eftersom den bestämmer antalet kanaler (linjer), volymen av utrustning för stationer och noder. Trafiken samma veckodag har säsongsvariationer. Om veckodagen är en förhelg, är NNN för denna dag högre än dagen efter helgdagen. I takt med att antalet tjänster som stöds av nätverket ökar, ökar också trafiken. Därför är det problematiskt att med tillräcklig säkerhet förutse förekomsten av trafiktoppar. Trafiken övervakas noga av nätverksadministration och designorganisationer. Trafikmätningsregler har utvecklats av ITU-T och används av nationella nätförvaltningar för att uppfylla tjänstekvalitetskraven för både abonnenter på deras nät och abonnenter på andra nät som är anslutna till det. Teletrafikteori kan användas för praktiska beräkningar av förluster eller volymen av stations(nod)utrustning endast om trafiken är stillastående (statistiskt stabil). Detta villkor är ungefär uppfyllt av trafiken i CHNN. Mängden last som kommer till den automatiska telefonväxeln per dag påverkar förebyggande och reparation av utrustning. Ojämnheten hos lasten som kommer in i stationen under dagen bestäms av koncentrationskoefficienten

En mer strikt definition av NNN görs enligt följande. ITU Rekommendation E.500 kräver att man analyserar 12 månaders intensitetsdata, väljer de 30 mest hektiska dagarna, hittar de mest hektiska timmarna på dessa dagar och medelvärdesmätningar av intensitetsmätningarna över dessa intervall. Denna beräkning av trafikintensitet (belastning) kallas en normal uppskattning av trafikintensitet i CHN eller nivå A. En strängare uppskattning kan beräknas i medeltal över de 5 mest trafikerade dagarna i den valda 30-dagarsperioden. Detta betyg kallas för höjt betyg eller betyg på nivå B.

Processen att skapa trafik. Som alla användare av telefonnätet vet är inte alla försök att upprätta en förbindelse med den uppringda abonnenten framgångsrika. Ibland måste du göra flera misslyckade försök innan den önskade anslutningen upprättas.

Figur 10. Diagram över händelser vid upprättande av en förbindelse mellan abonnenter

Låt oss överväga möjliga händelser när vi simulerar upprättandet av en förbindelse mellan abonnenter A och B (Figur 10). Statistik över samtal i telefonnät är följande: andelen avslutade samtal är 70-50%, andelen misslyckade samtal är 30-50%. Varje försök från abonnenten tar QS-ingången. Vid lyckade försök (när samtalet har ägt rum) är ockupationstiden för de kopplingsenheter som upprättar förbindelser mellan in- och utgångar längre än vid misslyckade försök. Abonnenten kan när som helst avbryta försök att upprätta en anslutning. Återförsök kan orsakas av följande orsaker:

Numret slogs felaktigt;

Antagande om ett fel i nätverket;

Graden av brådska i samtalet;

Misslyckade tidigare försök;

Att känna till abonnent B:s vanor;

Tvivlar på att slå numret rätt.

Ett nytt försök kan göras beroende på följande omständigheter:

Grader av brådska;

Bedömning av orsakerna till misslyckande;

Att bedöma genomförbarheten av upprepade försök,

Uppskattningar av acceptabelt intervall mellan försöken.

Om du inte försöker igen kan det bero på låg brådska. Det finns flera typer av trafik som genereras av samtal: inkommande (föreslagna) Y n och missade Y n Trafik Y n inkluderar alla lyckade och misslyckade försök, trafik Y n, som är en del av Y n, inkluderar framgångsrika och några misslyckade försök:

Y pr = Y r + Y np,

där Y p är konversationstrafik (användbar) och Y np är trafik som genereras av misslyckade försök. Likheten Yp = Yp är möjlig endast i det ideala fallet om det inte finns några förluster, fel genom att ringa abonnenter och inga svar från anropade abonnenter.

Skillnaden mellan inkommande och överförda laster över en viss tidsperiod blir den förlorade lasten.

Trafikprognos. Begränsade resurser leder till behov av en successiv utbyggnad av station och nätverk. Nätverksadministrationen förutspår en ökning av trafiken under utvecklingsfasen, med hänsyn till att:

Inkomsten bestäms av den del av den överförda trafiken Y p, - kostnaderna bestäms av tjänstekvaliteten med högst trafik;

En stor andel förluster (låg kvalitet) inträffar i sällsynta fall och är typiska för slutet av utvecklingsperioden;

Den största volymen av missad trafik uppstår under perioder då det praktiskt taget inte finns några förluster - om förlusterna är mindre än 10%, svarar inte abonnenterna på dem. Vid planering av utvecklingen av stationer och nätet ska konstruktören svara på frågan om vilka krav som ställs på kvaliteten på tillhandahållandet av tjänster (förluster). För att göra detta är det nödvändigt att mäta trafikförluster enligt de regler som antagits i landet.

Exempel på trafikmätning.

Låt oss först titta på hur du kan visa driften av en QS som har flera resurser som samtidigt betjänar viss trafik. Vi kommer vidare att prata om sådana resurser som servrar som tjänar flödet av applikationer eller krav. Ett av de mest visuella och ofta använda sätten att skildra processen för att betjäna förfrågningar av en pool av servrar är ett Gantt-diagram. Detta diagram är ett rektangulärt koordinatsystem där x-axeln visar tid och y-axeln markerar diskreta punkter som motsvarar poolservrarna. Figur 11 visar ett Gantt-diagram för ett system med tre servrar.

Under de tre första tidsintervallen (vi räknar dem som en andra) är den första och tredje servern upptagen, de kommande två sekunderna - bara den tredje, sedan fungerar den andra i en sekund, sedan den andra och den första i två sekunder , och de sista två sekunderna - bara den första.

Det konstruerade diagrammet låter dig beräkna trafikvolymen och dess intensitet. Diagrammet speglar endast serverad eller missad trafik, eftersom det inte säger något om huruvida förfrågningar kom in i systemet som inte kunde betjänas av servrarna.

Volymen av passerad trafik beräknas som den totala längden av alla segment i Gantt-diagrammet. Volym på 10 sekunder:

Vi associerar med varje tidsintervall, ritat på abskissan, ett heltal lika med antalet servrar som är upptagna i detta enhetsintervall. Detta värde A(t) är den momentana intensiteten. För vårt exempel

A(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Låt oss nu hitta den genomsnittliga trafikintensiteten under en period av 10 sekunder

Således är den genomsnittliga trafikintensiteten som passerar av systemet med tre servrar som är under övervägande 1,5 Erl.

Grundläggande belastningsparametrar

Telefonkommunikation används av olika kategorier av abonnenter, som kännetecknas av:

antal belastningskällor - N,

genomsnittligt antal samtal från en källa under en viss tid (vanligtvis NNN) - c,

den genomsnittliga varaktigheten av en session av växlingssystemet vid betjäning av ett samtal är t.

Belastningsintensiteten blir

Låt oss identifiera olika samtalskällor. Till exempel,

Genomsnittligt antal samtal till CHN från en kontorstelefon;

Genomsnittligt antal samtal från en enskild lägenhetstelefon; slumpmässig händelse masstjänst teletrafik

med räkning - samma från apparaten för kollektivt bruk;

med ma - samma från en myntmaskin;

med sl - samma från en anslutningsledning.

Sedan är det genomsnittliga antalet samtal från en källa:

Det finns ungefärliga uppgifter för det genomsnittliga antalet samtal från en källa i motsvarande kategori:

3,5 - 5, =0,5 - 1, med räkning = 1,5 - 2, med ma =15 - 30, med sl =10 - 30.

Det finns följande typer av anslutningar som, beroende på resultatet av anslutningen, skapar olika telefonbelastningar på stationen:

k р - koefficient som visar andelen anslutningar som slutade i konversation;

k з - anslutningar som inte slutade i konversation på grund av att den uppringda abonnenten var upptagen;

k men - koefficient som uttrycker andelen anslutningar som inte slutade i konversation på grund av att den uppringda abonnenten inte svarade;

k osh - anslutningar som inte slutade i konversation på grund av fel av den som ringer;

k de - samtal som inte slutade i samtal på grund av tekniska skäl.

Under normal nätverksdrift är värdena för dessa koefficienter lika med:

kp = 0,60-0,75; kz = 0,12-0,15; k men =0,08-0,12; k osh =0,02-0,05; k de =0,005-0,01.

Den genomsnittliga varaktigheten av en session beror på typen av anslutningar. Till exempel, om anslutningen avslutades med en konversation, kommer den genomsnittliga varaktigheten av enhetens ockupation t tillstånd att vara lika med

var är varaktigheten för upprättandet av anslutningen;

t komp. - ett samtal som ägde rum;

t - varaktighet för att skicka ett samtal till den uppringda abonnentens telefon;

t r - samtalets varaktighet

där tco är stationens svarssignal;

1.5n - tid för att slå numret till den uppringda abonnenten (n - antal tecken i numret);

t s är den tid som krävs för att upprätta en anslutning genom att byta mekanismer och koppla från anslutningen efter avslutat samtal. Ungefärliga värden för de övervägda kvantiteterna:

t co = 3 sek., tc = 1-2,5 sek., tb = 8-10 sek., t p = 90-130 sek.

Samtal som inte slutar i samtal skapar också telefonbelastning.

Den genomsnittliga tiden för att ockupera enheter när den uppringda abonnenten är upptagen är

där t installationsanslutning bestäms av (4.2.3)

t зз - tid för att lyssna på den upptagna summern, t зз =6 sek.

Den genomsnittliga varaktigheten av enhetens ockupation när den uppringda abonnenten inte svarar är

där t pv - tid för att lyssna på återringningssignalen, t pv = 20 sek.

Om det inte var något samtal på grund av abonnentfel, då i genomsnitt t osh = 30 sek.

Längden på klasser som inte slutade i samtal på grund av tekniska skäl är inte fastställd, eftersom andelen sådana klasser är liten.

Av allt ovanstående följer att den totala belastningen som skapas av en grupp källor bakom CNN är lika med summan av belastningarna av enskilda typer av aktiviteter.

var är en koefficient som tar hänsyn till villkoren som aktier

En automatisk telefonväxel har utformats på ett telefonnät med sjusiffrig numrering, vars struktur abonnenter är som följer:

N-konto = 4000, N ind = 1000, N-tal = 2000, N ma = 400, N sl = 400.

Det genomsnittliga antalet samtal som tas emot från en källa i CHNN är lika med

Med hjälp av formlerna (4.2.3) och (4.2.6) hittar vi lasten

1.10.62826767 sek. = 785,2 hz.

Genomsnittlig lektionslängd t från formeln Y=Nct

t= Y/Nc= 2826767/7800*3,8=95,4 sek.

Ladda uppgift

1. På ett telefonnät med sjusiffrig numrering är en automatisk telefonväxel utformad, vars strukturella sammansättning av abonnenter är som följer:

N uchr =5000, Nind=1500, N-tal =3000, N ma =500, Nsl =500.

Bestäm lasten som anländer till stationen - Y, den genomsnittliga varaktigheten av ockupationen t, om det är känt att

med ind =4, med ind =1, med räkning =2, med ma =10, med sl =12, t r =120 sek., t in =10 sek., k r = 0,6, t s = 1 sek., =1,1 .

Postat på Allbest.ru

Liknande dokument

Begreppet en enhetligt fördelad stokastisk variabel. Multiplikativ kongruent metod. Modellering av kontinuerliga slumpvariabler och diskreta distributioner. Algoritm för simulering av ekonomiska relationer mellan långivaren och låntagaren.

kursarbete, tillagd 2011-03-01


Allmänna begrepp inom köteori. Funktioner hos modellering av kösystem. Ange grafer för QS-system, ekvationer som beskriver dem. Allmänna egenskaper hos typer av modeller. Analys av ett stormarknadskösystem.

kursarbete, tillagd 2009-11-17


Inslag av köteori. Matematisk modellering av kösystem, deras klassificering. Simuleringsmodellering av kösystem. Praktisk tillämpning av teori, problemlösning med matematiska metoder.

kursarbete, tillagt 2011-04-05


Konceptet med en slumpmässig process. Problem med köteorin. Klassificering av kösystem (QS). Probabilistisk matematisk modell. Inverkan av slumpmässiga faktorer på ett objekts beteende. Enkanalig och flerkanalig QS med väntan.

kursarbete, tillagd 2014-09-25


Studie av de teoretiska aspekterna av effektiv konstruktion och drift av ett kösystem, dess huvudelement, klassificering, egenskaper och operativ effektivitet. Modellera ett kösystem med hjälp av GPSS-språket.

kursarbete, tillagt 2010-09-24


Utveckling av teorin om dynamisk programmering, nätverksplanering och produkttillverkning. Komponenter i spelteori i problem med modellering av ekonomiska processer. Inslag av praktisk tillämpning av köteori.

praktiskt arbete, tillagt 2011-08-01


Elementära begrepp om slumpmässiga händelser, kvantiteter och funktioner. Numeriska egenskaper hos slumpvariabler. Typer av distributionsasymmetri. Statistisk bedömning av fördelningen av stokastiska variabler. Lösa problem med strukturell-parametrisk identifiering.

kursarbete, tillagt 2012-06-03


Modellering av köprocessen. Olika kökanaler. Lösning av en enkanals kömodell med fel. Täthet av distribution av tjänstelängd. Bestämning av absolut genomströmning.

test, tillagt 2016-03-15


Funktionella egenskaper hos kösystemet inom vägtransportområdet, dess struktur och huvudelement. Kvantitativa indikatorer på kvaliteten på kösystemets funktion, ordningen och huvudstadierna för deras bestämning.

laboratoriearbete, tillagt 2011-11-03


Att sätta målet för modellering. Identifiering av verkliga föremål. Välja typ av modeller, matematiskt schema. Konstruktion av en kontinuerlig-stokastisk modell. Grundläggande begrepp inom köteori. Definiera flödet av händelser. Konfigurera algoritmer.