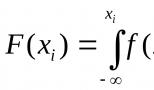Simulasi peristiwa rawak. Memainkan pembolehubah rawak berterusan. Kaedah fungsi songsang Mainkan lima nilai yang mungkin bagi pembolehubah rawak berterusan

Definisi 24.1.Nombor rawak namakan nilai yang mungkin r pembolehubah rawak berterusan R, diedarkan secara seragam dalam selang (0; 1).

1. Memainkan pembolehubah rawak diskret.

Katakan kita mahu memainkan pembolehubah rawak diskret X, iaitu, mendapatkan urutan nilai yang mungkin, mengetahui undang-undang pengedaran X:

X x 1 X 2 … x n

r r 1 R 2 … r p .

Pertimbangkan pembolehubah rawak teragih seragam dalam (0, 1) R dan bahagikan selang (0, 1) dengan titik dengan koordinat R 1, R 1 + R 2 , …, R 1 + R 2 +… +r p-1 pada P selang separa yang panjangnya sama dengan kebarangkalian dengan indeks yang sama.

Teorem 24.1. Jika setiap nombor rawak yang jatuh ke dalam selang diberikan nilai yang mungkin, maka nilai yang dimainkan akan mempunyai undang-undang pengedaran yang diberikan:

X x 1 X 2 … x n

r r 1 R 2 … r p .

Bukti.

Nilai kemungkinan pembolehubah rawak yang terhasil bertepatan dengan set X 1 , X 2 ,… x n, kerana bilangan selang adalah sama P, dan apabila terkena r j dalam selang waktu, pembolehubah rawak boleh mengambil hanya satu daripada nilai X 1 , X 2 ,… x n.

Kerana R diedarkan secara seragam, maka kebarangkalian ia jatuh ke dalam setiap selang adalah sama dengan panjangnya, yang bermaksud bahawa setiap nilai sepadan dengan kebarangkalian p i. Oleh itu, pembolehubah rawak yang dimainkan mempunyai hukum taburan yang diberikan.

Contoh. Mainkan 10 nilai pembolehubah rawak diskret X, undang-undang pengedaran yang mempunyai bentuk: X 2 3 6 8

R 0,1 0,3 0,5 0,1

Penyelesaian. Mari bahagikan selang (0, 1) kepada selang separa: D 1 - (0; 0.1), D 2 - (0.1; 0.4), D 3 - (0.4; 0.9), D 4 – (0.9; 1). Mari kita tulis 10 nombor daripada jadual nombor rawak: 0.09; 0.73; 0.25; 0.33; 0.76; 0.52; 0.01; 0.35; 0.86; 0.34. Nombor pertama dan ketujuh terletak pada selang D 1, oleh itu, dalam kes ini, pembolehubah rawak yang dimainkan mengambil nilai X 1 = 2; nombor ketiga, keempat, kelapan dan kesepuluh jatuh ke dalam selang D 2, yang sepadan dengan X 2 = 3; nombor kedua, kelima, keenam dan kesembilan berada dalam selang D 3 - dalam kes ini X = x 3 = 6; Tiada nombor dalam selang terakhir. Jadi, nilai yang mungkin dimainkan X ialah: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. Melakonkan peristiwa yang bertentangan.

Biarkan ia dikehendaki memainkan ujian, dalam setiap satu acara A muncul dengan kebarangkalian yang diketahui R. Pertimbangkan pembolehubah rawak diskret X, mengambil nilai 1 (jika acara A berlaku) dengan kebarangkalian R dan 0 (jika A tidak berlaku) dengan kebarangkalian q = 1 – hlm. Kemudian kita akan memainkan pembolehubah rawak ini seperti yang dicadangkan dalam perenggan sebelumnya.

Contoh. Main 10 cabaran, setiap satu dengan acara A muncul dengan kebarangkalian 0.3.

Penyelesaian. Untuk pembolehubah rawak X dengan hukum pengagihan X 1 0

R 0,3 0,7

kita memperoleh selang D 1 – (0; 0.3) dan D 2 – (0.3; 1). Kami menggunakan sampel nombor rawak yang sama seperti dalam contoh sebelumnya, yang mana nombor No. 1, 3 dan 7 jatuh ke dalam selang D 1, dan selebihnya - ke dalam selang D 2. Oleh itu, kita boleh menganggap bahawa peristiwa itu A berlaku dalam percubaan pertama, ketiga dan ketujuh, tetapi tidak berlaku dalam percubaan yang selebihnya.

3. Memainkan kumpulan acara yang lengkap.

Jika peristiwa A 1 , A 2 , …, A p, yang kebarangkaliannya adalah sama R 1 , R 2 ,… r p, membentuk kumpulan yang lengkap, kemudian untuk bermain (iaitu, memodelkan urutan penampilan mereka dalam satu siri ujian), anda boleh memainkan pembolehubah rawak diskret X dengan hukum pengagihan X 1 2 … P, setelah melakukan ini dengan cara yang sama seperti dalam perkara 1. Pada masa yang sama, kami percaya bahawa

r r 1 R 2 … r p

Jika X mengambil nilai x i = i, maka dalam ujian ini peristiwa itu berlaku A i.

4. Memainkan pembolehubah rawak berterusan.

a) Kaedah fungsi songsang.

Katakan kita mahu memainkan pembolehubah rawak berterusan X, iaitu, dapatkan urutan nilai yang mungkin x i (i = 1, 2, …, n), mengetahui fungsi pengedaran F(x).

Teorem 24.2. Jika r i ialah nombor rawak, maka nilai yang mungkin x i dimainkan pembolehubah rawak berterusan X dengan fungsi pengedaran tertentu F(x), sepadan r i, ialah punca persamaan

F(x i) = r i. (24.1)

Bukti.

Kerana F(x) meningkat secara monoton dalam selang dari 0 hingga 1, maka terdapat nilai (dan unik) bagi argumen x i, di mana fungsi pengedaran mengambil nilai r i. Ini bermakna persamaan (24.1) mempunyai penyelesaian yang unik: x i= F -1 (r i), Di mana F-1 - fungsi songsang kepada F. Mari kita buktikan bahawa punca persamaan (24.1) ialah nilai yang mungkin bagi pembolehubah rawak yang sedang dipertimbangkan X. Mari kita andaikan dahulu x i ialah nilai yang mungkin bagi beberapa pembolehubah rawak x, dan kami membuktikan bahawa kebarangkalian x jatuh ke dalam selang ( s, d) adalah sama dengan F(d) – F(c). Memang, kerana monotoni F(x) dan itu F(x i) = r i. Kemudian

Oleh itu, Jadi, kebarangkalian x jatuh ke dalam selang ( c,d) adalah sama dengan pertambahan fungsi pengagihan F(x) pada selang ini, oleh itu, x = X.

Mainkan 3 kemungkinan nilai pembolehubah rawak berterusan X, diedarkan secara seragam dalam selang (5; 8).

F(x) = , iaitu perlu menyelesaikan persamaan Mari kita pilih 3 nombor rawak: 0.23; 0.09 dan 0.56 dan gantikannya ke dalam persamaan ini. Mari dapatkan nilai yang mungkin sepadan X:

b) Kaedah superposisi.

Jika fungsi taburan pembolehubah rawak yang dimainkan boleh diwakili sebagai gabungan linear dua fungsi taburan:

kemudian, sejak bila X®¥ F(x) ® 1.

Mari kita perkenalkan pembolehubah rawak diskret tambahan Z dengan hukum pengagihan

Z 12 . Mari pilih 2 nombor rawak bebas r 1 dan r 2 dan bermain yang mungkin

pC 1 C 2

maksudnya Z mengikut nombor r 1 (lihat titik 1). Jika Z= 1, kemudian kita mencari nilai yang mungkin dikehendaki X daripada persamaan, dan jika Z= 2, maka kita selesaikan persamaan .

Dapat dibuktikan bahawa dalam kes ini fungsi taburan pembolehubah rawak yang dimainkan adalah sama dengan fungsi taburan yang diberikan.

c) Anggaran permainan pembolehubah rawak normal.

Memandangkan R, diedarkan secara seragam dalam (0, 1), kemudian untuk jumlahnya P bebas, pembolehubah rawak teragih seragam dalam selang (0,1). Kemudian, berdasarkan teorem had pusat, pembolehubah rawak ternormal pada P® ¥ akan mempunyai taburan hampir kepada normal, dengan parameter A= 0 dan s =1. Khususnya, anggaran yang agak baik diperoleh apabila P = 12:

Jadi, untuk memainkan nilai yang mungkin bagi pembolehubah rawak normal ternormal X, anda perlu menambah 12 nombor rawak bebas dan tolak 6 daripada jumlah itu.

Kaedah fungsi songsang

Katakan kita mahu memainkan pembolehubah rawak berterusan X, iaitu dapatkan urutan nilai yang mungkin x i (i= 1,2, ...), mengetahui fungsi taburan F(X).

Teorem. Jika r i ,-nombor rawak, kemudian nilai yang mungkinx i memainkan pembolehubah rawak berterusan X dengan fungsi taburan yang diberikanF(X), sepadanr i , ialah punca persamaan

F(X i)= r i . (»)

Bukti. Biarkan nombor rawak dipilih r i (0≤r i <1). Так как в интервале всех возможных зна­чений X fungsi pengagihan F(X) monotonik meningkat daripada 0 kepada 1, maka dalam selang ini terdapat, dan hanya satu, nilai hujah sedemikian X i , di mana fungsi pengedaran mengambil nilai r i. Dengan kata lain, persamaan (*) mempunyai penyelesaian yang unik

X i = F - 1 (r i),

di mana F - 1 - fungsi songsang y=F(X).

Mari kita buktikan bahawa akarnya X i persamaan (*) ialah nilai yang mungkin bagi pembolehubah rawak berterusan sedemikian (kami akan menandakannya buat sementara waktu dengan ξ , dan kemudian kami akan memastikannya ξ=Х). Untuk tujuan ini, kami membuktikan bahawa kebarangkalian memukul ξ ke dalam selang waktu, contohnya ( dengan,d), tergolong dalam selang semua nilai yang mungkin X, sama dengan kenaikan fungsi pengedaran F(X) pada selang waktu ini:

R(Dengan< ξ < d)= F(d)- F(Dengan).

Memang sejak F(X)- monotoni meningkatkan fungsi dalam selang semua nilai yang mungkin X, maka dalam selang ini nilai besar argumen sepadan dengan nilai besar fungsi, dan sebaliknya. Oleh itu, jika Dengan <X i < d, Itu F(c)< r i < F(d), dan sebaliknya [diambil kira bahawa disebabkan oleh (*) F(X i)=r i ].

Daripada ketaksamaan ini berikutan bahawa jika pembolehubah rawak ξ terkandung dalam selang

Dengan< ξ < d, ξ (**)

kemudian pembolehubah rawak R terkandung dalam selang

F(Dengan)< R< F(d), (***)

dan kembali. Oleh itu, ketaksamaan (**) dan (***) adalah setara dan, oleh itu, berkemungkinan sama:

R(Dengan< ξ< d)=P[F(Dengan)< R< F(d)]. (****)

Sejak nilai R diedarkan secara seragam dalam selang (0,1), maka kebarangkalian untuk memukul R ke dalam beberapa selang kepunyaan selang (0,1) adalah sama dengan panjangnya (lihat Bab XI, § 6, catatan). khususnya,

R[F(Dengan)< R< F(d) ] = F(d) - F(Dengan).

Oleh itu, hubungan (****) boleh ditulis dalam bentuk

R(Dengan< ξ< d)= F(d) - F(Dengan).

Jadi, kebarangkalian untuk memukul ξ dalam selang waktu ( dengan,d) adalah sama dengan pertambahan fungsi taburan F(X) pada selang ini, yang bermaksud bahawa ξ=X. Dalam erti kata lain, nombor X i, ditakrifkan oleh formula (*), ialah nilai kuantiti yang mungkin X s fungsi pengagihan yang diberikan F(X), Q.E.D.

Peraturan 1.X i , pembolehubah rawak berterusan X, mengetahui fungsi pengedarannya F(X), anda perlu memilih nombor rawak r i samakan fungsi pengedarannya dan selesaikan untuk X i , persamaan yang terhasil

F(X i)= r i .

Catatan 1. Jika tidak dapat menyelesaikan persamaan ini secara eksplisit, maka gunakan kaedah grafik atau berangka.

Contoh I. Mainkan 3 kemungkinan nilai pembolehubah rawak berterusan X, diedarkan secara seragam dalam selang (2, 10).

Penyelesaian. Mari kita tulis fungsi taburan kuantiti X, diedarkan secara seragam dalam selang waktu ( A,b) (lihat Bab XI, § 3, contoh):

F(X)= (Ha)/ (b-A).

Dengan syarat, a = 2, b=10, oleh itu,

F(X)= (X- 2)/ 8.

Menggunakan peraturan perenggan ini, kita akan menulis persamaan untuk mencari nilai yang mungkin X i , yang mana kita menyamakan fungsi pengedaran dengan nombor rawak:

(X i -2 )/8= r i .

Dari sini X i =8 r i + 2.

Mari kita pilih 3 nombor rawak, sebagai contoh, r i =0,11, r i =0,17, r i=0.66. Mari kita gantikan nombor ini ke dalam persamaan yang diselesaikan berkenaan dengan X i , Akibatnya, kami mendapat nilai yang mungkin sepadan X: X 1 =8·0.11+2==2.88; X 2 =1.36; X 3 = 7,28.

Contoh 2. Pembolehubah rawak berterusan X diedarkan mengikut undang-undang eksponen yang ditentukan oleh fungsi pengedaran (parameter λ > 0 diketahui)

F(X)= 1 - e - λ X (x>0).

Kita perlu mencari formula yang jelas untuk memainkan nilai yang mungkin X.

Penyelesaian. Menggunakan peraturan perenggan ini, kami menulis persamaan

1 - e - λ X i

Mari kita selesaikan persamaan ini untuk X i :

e - λ X i = 1 - r i, atau - λ X i = ln(1 - r i).

X i =1p(1– r i)/λ .

Nombor rawak r i disertakan dalam selang (0,1); oleh itu nombor 1 ialah r i, juga rawak dan tergolong dalam selang (0,1). Dalam erti kata lain, kuantiti R dan 1 - R sama rata. Oleh itu, untuk mencari X i Anda boleh menggunakan formula yang lebih mudah:

x i =- ln r i /λ.

Catatan 2. Adalah diketahui bahawa (lihat Bab XI, §3)

khususnya,

Ia berikutan bahawa jika ketumpatan kebarangkalian diketahui f(x), kemudian untuk bermain X ia adalah mungkin dan bukannya persamaan F(x i)=r i memutuskan mengenai x i persamaan

Peraturan 2. Untuk mencari nilai yang mungkin X i (pembolehubah rawak berterusan X, mengetahui ketumpatan kebarangkaliannya f(x) anda perlu memilih nombor rawak r i dan memutuskan mengenai X i , persamaan

atau persamaan

di mana A- nilai akhir terkecil yang mungkin X.

Contoh 3. Ketumpatan kebarangkalian pembolehubah rawak berterusan diberikan Xf(X)=λ (1-λх/2) dalam selang (0; 2/λ); di luar selang ini f(X)= 0. Kita perlu mencari formula eksplisit untuk memainkan nilai yang mungkin X.

Penyelesaian. Selaras dengan peraturan 2, mari kita tulis persamaan

Selepas melakukan pengamiran dan menyelesaikan persamaan kuadratik yang terhasil untuk X i, akhirnya kita dapat

Mari kita ingat dahulu bahawa jika pembolehubah rawak R diedarkan secara seragam dalam selang (0,1), maka jangkaan dan varians matematiknya masing-masing adalah sama (lihat Bab XII, § 1, catatan 3):

M(R)= 1/2, (*)

D(R)= 1/2. (**)

Mari kita buat jumlah P pembolehubah rawak bebas diedarkan secara seragam dalam selang (0,1) R j(j=1, 2, ...,n):

Untuk menormalkan jumlah ini, kita mula-mula mencari jangkaan dan varians matematiknya.

Adalah diketahui bahawa jangkaan matematik jumlah pembolehubah rawak adalah sama dengan jumlah jangkaan matematik istilah. Jumlah (***) mengandungi P istilah, jangkaan matematik setiap satunya disebabkan oleh (*) adalah sama dengan 1/2; oleh itu, jangkaan matematik jumlah ( *** )

Adalah diketahui bahawa varians jumlah pembolehubah rawak bebas adalah sama dengan jumlah varians istilah. Jumlah (***) mengandungi n istilah bebas, serakan setiap satunya, disebabkan oleh (**), bersamaan dengan 1/12; maka varians jumlah (***)

Oleh itu sisihan piawai jumlah (***)

Marilah kita menormalkan jumlah yang sedang dipertimbangkan, yang mana kita menolak jangkaan matematik dan membahagikan hasilnya dengan sisihan piawai:

Berdasarkan teorem had pusat, apabila p→∞ taburan pembolehubah rawak ternormal ini cenderung kepada normal dengan parameter a= 0 dan σ=1. Pada akhir P taburan adalah lebih kurang normal. Khususnya, apabila P= 12 kita memperoleh anggaran yang agak baik dan mudah untuk pengiraan

peraturan. Untuk memainkan nilai yang mungkin x i pembolehubah rawak biasa X dengan parameter a=0 dan σ=1, anda perlu menambah 12 nombor rawak bebas dan tolak 6 daripada jumlah yang terhasil:

contoh, a) Mainkan 100 nilai yang mungkin daripada nilai normal X dengan parameter a=0 dan σ=1; b) menganggarkan parameter nilai yang dimainkan.

Penyelesaian. a) Mari pilih 12 nombor rawak daripada baris pertama jadual *), tambahkan dan tolak 6 daripada jumlah yang terhasil; akhirnya kita ada

x i=(0,10+0,09+...+0,67) - 6= - 0,99.

Begitu juga, dengan memilih 12 nombor pertama daripada setiap baris seterusnya jadual, kita akan mencari nilai yang mungkin selebihnya. X.

b) Selepas melakukan pengiraan, kami memperoleh anggaran yang diperlukan:

Penilaian yang memuaskan: A* menghampiri sifar, σ* berbeza sedikit dengan perpaduan.

Komen. Jika anda ingin memainkan nilai yang mungkin z i, pembolehubah rawak normal Z dengan jangkaan matematik A dan sisihan piawai σ , maka, setelah bermain mengikut peraturan perenggan ini nilai yang mungkin xi, cari nilai kemungkinan yang dikehendaki menggunakan formula

z i =σx i +a.

Formula ini diperoleh daripada hubungan ( z i -a)/σ=x i.

Tugasan

1. Mainkan 6 nilai pembolehubah rawak diskret X, hukum taburan yang diberikan dalam bentuk jadual

Catatan. Untuk memastikan, andaikan nombor rawak telah dipilih: 0.73; 0.75; 0.54; 0.08; 0.28; 0.53. Rep. 10; 10; 10; 2; 3; 22; 10.

2. Main 4 percubaan, setiap satu dengan kebarangkalian sesuatu peristiwa berlaku A bersamaan dengan 0.52.

Catatan. Untuk memastikan, andaikan nombor rawak telah dipilih: 0;28; 0.53; 0.91; 0.89.

Rep. A, , .

3. Kebarangkalian bagi tiga peristiwa membentuk kumpulan lengkap diberi: R(A 1)=0,20, R(A 2)=0,32, R(A 3)= 0,48. Main 6 cabaran, di mana setiap satu daripada acara yang diberikan muncul.

Catatan. Untuk memastikan, andaikan nombor rawak telah dipilih: 0.77; 0.19; 0.21; 0.51; 0.99; 0.33.

Rep. A 3,A 1 ,A 2 ,A 2 ,A 3,A 2 .

4. Peristiwa A dan B berdikari dan bekerjasama. Main 5 cabaran, setiap satu dengan kebarangkalian kejadian berlaku A adalah sama dengan 0.5, dan peristiwa DALAM- 0,8.

A 1 =AB, untuk kepastian, ambil nombor rawak: 0.34; 0.41; 0.48; 0.21; 0.57.

Rep. A 1 ,A 2 ,A 2 ,A 1 ,A 3.

5. Peristiwa A, B, C berdikari dan bekerjasama. Main 4 ujian di mana setiap satu kebarangkalian berlakunya peristiwa diberikan: R(A)= 0,4, R(DALAM)= 0,6, R(DENGAN)= 0,5.

Catatan. Susun kumpulan acara yang lengkap: untuk kepastian, anggap nombor rawak dipilih: 0.075; 0.907; 0.401; 0.344.

Jawapan A 1 ,A 8,A 4,A 4.

6. Peristiwa A Dan DALAM bergantung dan bekerjasama. Main 4 ujian, setiap satunya telah memberikan kebarangkalian: R(A)=0,7, R(DALAM)=0,6, R(AB)=0,4.

Catatan. Buat kumpulan acara yang lengkap: A 1 =AB, untuk kepastian, ambil nombor rawak: 0.28; 0.53; 0.91; 0.89.

Rep. A 1 , A 2 , A 4 , A 3 .

7. Mainkan 3 kemungkinan nilai pembolehubah rawak berterusan X, yang diedarkan mengikut undang-undang eksponen dan ditentukan oleh fungsi pengedaran F(X)= 1 - e -10 x .

Catatan. Untuk kepastian, andaikan nombor rawak telah dipilih: 0.67; 0.79; 0.91.

Rep. 0,04; 0,02; 0,009.

8. Mainkan 4 kemungkinan nilai pembolehubah rawak berterusan X, diedarkan secara seragam dalam selang (6,14).

Catatan. Untuk kepastian, andaikan nombor rawak telah dipilih: 0.11: 0.04; 0.61; 0.93.

Rep. 6,88; 6,32; 10,88; 13,44.

9. Cari formula eksplisit untuk memainkan pembolehubah rawak berterusan menggunakan kaedah superposisi X, fungsi pengagihan yang diberikan

F(x)=1- (1/3)(2е- 2 x +е -3 x:), 0<X<∞.

Rep. x= - (1/2)1п r 2 jika r 1 < 2/3; X= - (1/3)1п r 2 jika r 1 ≥2/3.

10. Cari formula eksplisit untuk memainkan pembolehubah rawak berterusan X, diberi kepadatan kebarangkalian f(X)=b/(1 +kapak) 2 dalam selang 0≤ x≤1/(b-a); di luar selang ini f(x)=0.

Rep. x i= - r i/(b - ar i).

11. Mainkan 2 kemungkinan nilai pembolehubah rawak normal dengan parameter: a) A=0, σ =1; b) A =2, σ =3.

Catatan. Untuk kepastian, terima nombor rawak (bilangan perseratus ditunjukkan di bawah; contohnya, nombor 74 sepadan dengan nombor rawak r 1 =0,74): 74. 10, 88, 82. 22, 88, 57, 07, 40, 15, 25, 70; 62, 88, 08, 78, 73, 95, 16, 05, 92, 21, 22, 30.

Rep. A) x 1 = - 0,22, x 2 = - 0.10; 6) z 1 =1,34, z 2 =2,70.

Bab dua puluh dua

Biarkan ia dikehendaki memainkan pembolehubah rawak berterusan X, i.e. dapatkan urutan nilai yang mungkin (i=1, 2, ..., n), mengetahui fungsi taburan F(x).

Teorem. Jika ialah nombor rawak, maka nilai kemungkinan pembolehubah rawak selanjar X yang dimainkan dengan fungsi taburan F (x), sepadan dengan , ialah punca persamaan.

Peraturan 1. Untuk mencari nilai yang mungkin, pembolehubah rawak berterusan X, mengetahui fungsi taburannya F (x), anda perlu memilih nombor rawak, menyamakan fungsi taburannya dan menyelesaikan persamaan yang terhasil.

Nota 1. Jika tidak mungkin untuk menyelesaikan persamaan ini secara eksplisit, maka gunakan kaedah grafik atau berangka.

Contoh 1. Mainkan 3 nilai yang mungkin bagi pembolehubah rawak berterusan X, diedarkan secara seragam dalam selang (2, 10).

Penyelesaian: Mari kita tulis fungsi taburan bagi nilai X, diedarkan secara seragam dalam selang (a, b): .

Mengikut keadaan, a=2, b=10, oleh itu, .

Menggunakan peraturan 1, kita akan menulis persamaan untuk mencari nilai yang mungkin, yang mana kita menyamakan fungsi taburan kepada nombor rawak:

Dari sini .

Mari kita pilih 3 nombor rawak, sebagai contoh, . Mari kita gantikan nombor ini ke dalam persamaan yang diselesaikan berkenaan dengan ; Akibatnya, kami memperoleh kemungkinan nilai X yang sepadan: ; ; .

Contoh 2. Pembolehubah rawak berterusan X diedarkan mengikut hukum eksponen yang ditentukan oleh fungsi taburan (parameter diketahui) (x > 0). Kita perlu mencari formula eksplisit untuk memainkan kemungkinan nilai X.

Penyelesaian: Dengan menggunakan peraturan, kita tulis persamaan.

Mari selesaikan persamaan ini untuk: , atau .

Nombor rawak terkandung dalam selang (0, 1); oleh itu, nombor itu juga rawak dan tergolong dalam selang (0,1). Dengan kata lain, nilai R dan 1-R diagihkan sama rata. Oleh itu, untuk mencarinya, anda boleh menggunakan formula yang lebih mudah.

Nota 2. Adalah diketahui bahawa .

Secara khususnya, .

Ia berikutan bahawa jika ketumpatan kebarangkalian diketahui, maka untuk memainkan X, bukannya persamaan, seseorang boleh menyelesaikan persamaan .

Peraturan 2. Untuk mencari nilai kemungkinan pembolehubah rawak berterusan X, mengetahui ketumpatan kebarangkaliannya, adalah perlu untuk memilih nombor rawak dan menyelesaikannya persamaan atau persamaan , di mana a ialah nilai terkecil yang mungkin terkecil bagi X.

Contoh 3. Ketumpatan kebarangkalian pembolehubah rawak berterusan X dalam selang diberikan; di luar selang ini. Kita perlu mencari formula eksplisit untuk memainkan kemungkinan nilai X.

Penyelesaian: Mari kita tulis persamaan mengikut peraturan 2.

Selepas melakukan pengamiran dan menyelesaikan persamaan kuadratik yang terhasil untuk , akhirnya kita akan dapat.

18.7 Anggaran permainan pembolehubah rawak biasa

Mari kita ingat dahulu bahawa jika pembolehubah rawak R diedarkan secara seragam dalam selang (0, 1), maka jangkaan dan varians matematiknya masing-masing adalah sama: M(R)=1/2, D(R)=1/12.

Mari kita kumpulkan hasil tambah n pembolehubah rawak teragih seragam dalam selang (0, 1): .

Untuk menormalkan jumlah ini, kita mula-mula mencari jangkaan dan varians matematiknya.

Adalah diketahui bahawa jangkaan matematik jumlah pembolehubah rawak adalah sama dengan jumlah jangkaan matematik istilah. Jumlahnya mengandungi n sebutan, jangkaan matematik setiap satunya, disebabkan oleh M(R) = 1/2, bersamaan dengan 1/2; oleh itu, jangkaan matematik jumlah

Adalah diketahui bahawa varians jumlah pembolehubah rawak bebas adalah sama dengan jumlah varians istilah. Jumlahnya mengandungi n sebutan bebas, varians setiap satunya, disebabkan oleh D(R) = 1/12, adalah sama dengan 1/12; oleh itu, varians jumlah

Oleh itu sisihan piawai jumlah

Mari kita normalkan amaun yang sedang dipertimbangkan, yang mana kita tolak jangkaan matematik dan bahagikan hasilnya dengan sisihan piawai: .

Berdasarkan teorem had pusat, taburan pembolehubah rawak ternormal ini cenderung kepada normal dengan parameter a = 0 dan . Untuk n terhingga, taburan adalah lebih kurang normal. Khususnya, untuk n=12 kita memperoleh anggaran yang agak baik dan mudah untuk pengiraan.

Anggaran adalah memuaskan: hampir kepada sifar, sedikit berbeza daripada satu.

Senarai sumber yang digunakan

1. Gmurman V.E. Teori Kebarangkalian dan Statistik Matematik. – M.: Sekolah Tinggi, 2001.

2. Kalinina V.N., Pankin V.F. perangkaan matematik. – M.: Sekolah Tinggi, 2001.

3. Gmurman V.E. Panduan untuk menyelesaikan masalah dalam teori kebarangkalian dan statistik matematik. – M.: Sekolah Tinggi, 2001.

4. Kochetkov E.S., Smerchinskaya S.O., Sokolov V.V. Teori Kebarangkalian dan Statistik Matematik. – M.:FORUM:INFRA-M, 2003.

5. Agapov G.I. Buku masalah mengenai teori kebarangkalian. – M.: Sekolah Tinggi, 1994.

6. Kolemaev V.A., Kalinina V.N. Teori Kebarangkalian dan Statistik Matematik. – M.: INFRA-M, 2001.

7. Ventzel E.S. Teori kebarangkalian. – M.: Sekolah Tinggi, 2001.

Hantar kerja baik anda di pangkalan pengetahuan adalah mudah. Gunakan borang di bawah

Pelajar, pelajar siswazah, saintis muda yang menggunakan asas pengetahuan dalam pengajian dan kerja mereka akan sangat berterima kasih kepada anda.

Disiarkan di http://www.allbest.ru/

PELAJARAN 1

Simulasi peristiwa rawak dengan undang-undang taburan yang diberikan

Memainkan Pembolehubah Rawak Diskret

Biarkan perlu memainkan pembolehubah rawak diskret, i.e. dapatkan urutan nilai yang mungkin x i (i = 1,2,3,...n), mengetahui hukum taburan X:

Mari kita nyatakan dengan R suatu pembolehubah rawak selanjar. Nilai R diedarkan secara seragam dalam selang (0,1). Dengan r j (j = 1,2,...) kita menandakan nilai yang mungkin bagi pembolehubah rawak R. Mari kita bahagikan selang 0< R < 1 на оси 0r точками с координатами на n частичных интервалов.

Kemudian kita dapat:

Dapat dilihat bahawa panjang selang separa dengan indeks i adalah sama dengan kebarangkalian P dengan indeks yang sama. Panjang

Oleh itu, apabila nombor rawak r i jatuh ke dalam selang, pembolehubah rawak X mengambil nilai x i dengan kebarangkalian P i .

Terdapat teorem berikut:

Jika setiap nombor rawak yang jatuh ke dalam selang dikaitkan dengan nilai yang mungkin x i , maka nilai yang dimainkan akan mempunyai undang-undang taburan yang diberikan

Algoritma untuk memainkan pembolehubah rawak diskret yang ditentukan oleh undang-undang taburan

1. Adalah perlu untuk membahagikan selang (0,1) paksi 0r kepada n separa separa:

2. Pilih (contohnya, daripada jadual nombor rawak, atau pada komputer) nombor rawak r j .

Jika r j jatuh ke dalam selang, maka pembolehubah rawak diskret yang dimainkan mengambil nilai yang mungkin x i .

Memainkan Pembolehubah Rawak Berterusan

Biarkan ia dikehendaki memainkan pembolehubah rawak berterusan X, i.e. dapatkan urutan nilai yang mungkin x i (i = 1,2,...). Dalam kes ini, fungsi taburan F(X) diketahui.

wujud seterusnya teorem.

Jika r i ialah nombor rawak, maka nilai yang mungkin x i bagi pembolehubah rawak berterusan X yang dimainkan dengan fungsi taburan F(X) yang diketahui bersamaan dengan r i ialah punca persamaan.

Algoritma untuk memainkan pembolehubah rawak berterusan:

1. Anda mesti memilih nombor rawak r i .

2. Samakan nombor rawak yang dipilih dengan fungsi taburan F(X) yang diketahui dan dapatkan persamaan.

3. Selesaikan persamaan ini untuk x i. Nilai x i yang terhasil pada masa yang sama akan sepadan dengan nombor rawak r i . dan hukum pengagihan yang diberikan F(X).

Contoh. Mainkan 3 nilai yang mungkin bagi pembolehubah rawak berterusan X, diedarkan secara seragam dalam selang (2; 10).

Fungsi taburan nilai X mempunyai bentuk berikut:

Dengan syarat, a = 2, b = 10, oleh itu,

Selaras dengan algoritma untuk memainkan pembolehubah rawak berterusan, kita menyamakan F(X) dengan nombor rawak yang dipilih r i .. Kita dapat dari sini:

Gantikan nombor-nombor ini ke dalam persamaan (5.3) Kami memperoleh nilai yang mungkin sepadan bagi x:

Masalah memodelkan peristiwa rawak dengan undang-undang taburan yang diberikan

1. Ia dikehendaki memainkan 10 nilai pembolehubah rawak diskret, i.e. dapatkan urutan nilai yang mungkin x i (i=1,2,3,…n), mengetahui hukum taburan X

Mari kita pilih nombor rawak r j daripada jadual nombor rawak: 0.10; 0.12; 0.37; 0.09; 0.65; 0.66; 0.99; 0.19; 0.88; 0.59; 0.78

2. Kekerapan penerimaan permintaan untuk perkhidmatan adalah tertakluk kepada undang-undang pengedaran eksponen (), x, parameter l diketahui (selepas ini l = 1/t - keamatan penerimaan permintaan)

l=0.5 permintaan/jam. Tentukan urutan nilai untuk tempoh selang antara penerimaan permohonan. Bilangan pelaksanaan ialah 5. Bilangan r j: 0.10; 0.12; 0.37; 0.09; 0.65; 0.99;

PELAJARAN 2

Sistem beratur

Sistem di mana, dalam satu pihak, terdapat permintaan besar-besaran untuk prestasi apa-apa jenis perkhidmatan, dan sebaliknya, permintaan ini dipenuhi, dipanggil sistem beratur. Mana-mana QS berfungsi untuk memenuhi aliran permintaan.

QS termasuk: sumber permintaan, aliran masuk, baris gilir, peranti penyajian, aliran keluar permintaan.

SMO dibahagikan kepada:

QS dengan kerugian (kegagalan)

Beratur dengan menunggu (panjang giliran tanpa had)

QS dengan panjang giliran terhad

QS dengan masa menunggu yang terhad.

Berdasarkan bilangan saluran atau peranti perkhidmatan, sistem QS boleh menjadi saluran tunggal atau berbilang saluran.

Mengikut lokasi sumber keperluan: terbuka dan tertutup.

Mengikut bilangan elemen perkhidmatan setiap keperluan: fasa tunggal dan berbilang fasa.

Salah satu bentuk pengelasan ialah pengelasan D. Kendall - A/B/X/Y/Z

A - menentukan pengagihan masa antara ketibaan;

B - menentukan pengagihan masa perkhidmatan;

X - menentukan bilangan saluran perkhidmatan;

Y - menentukan kapasiti sistem (panjang giliran);

Z - menentukan susunan perkhidmatan.

Apabila kapasiti sistem tidak terhingga dan baris gilir perkhidmatan mengikut prinsip siapa cepat dia dapat, bahagian Y/Z akan ditinggalkan. Digit pertama (A) menggunakan simbol berikut:

Taburan M mempunyai undang-undang eksponen,

G-ketiadaan sebarang andaian tentang proses perkhidmatan, atau ia dikenal pasti dengan simbol GI, yang bermaksud proses perkhidmatan berulang,

D- deterministik (masa perkhidmatan tetap),

E n - Pesanan ke- Erlang,

NM n - pesanan ke-n hyper-Erlang.

Digit kedua (B) menggunakan simbol yang sama.

Digit keempat (Y) menunjukkan kapasiti penimbal, i.e. bilangan maksimum tempat dalam baris gilir.

Angka kelima (Z) menunjukkan kaedah pemilihan daripada baris gilir dalam sistem menunggu: SP-kebarangkalian sama, FF-first-in-first out, LF-last-in-first out, PR-priority.

Untuk tugasan:

l ialah purata bilangan permohonan yang diterima setiap unit masa

µ - purata bilangan permintaan yang disampaikan setiap unit masa

Faktor beban saluran 1, atau peratusan masa saluran sibuk.

Ciri-ciri utama:

1) P tolak - kebarangkalian kegagalan - kebarangkalian bahawa sistem akan menolak perkhidmatan dan keperluan hilang. Ini berlaku apabila saluran atau semua saluran sibuk (TFoP).

Untuk QS P berbilang saluran terbuka =P n, dengan n ialah bilangan saluran perkhidmatan.

Untuk QS dengan panjang baris gilir terhad P buka =P n + l, dengan l ialah panjang baris gilir yang dibenarkan.

2) q relatif dan kapasiti sistem mutlak A

q= 1-P buka A=ql

3) Jumlah bilangan keperluan dalam sistem

L sys = n - untuk SMO dengan kegagalan, n ialah bilangan saluran yang diduduki oleh servis.

Untuk QS dengan menunggu dan panjang giliran terhad

L sys = n+L sejuk

dengan L cool ialah purata bilangan permintaan yang menunggu perkhidmatan dimulakan, dsb.

Kami akan mempertimbangkan ciri-ciri yang tinggal semasa kami menyelesaikan masalah.

Sistem beratur satu saluran dan berbilang saluran. Sistem dengan kegagalan.

Model saluran tunggal yang paling mudah dengan aliran input dan prosedur perkhidmatan kemungkinan ialah model yang dicirikan oleh taburan eksponen bagi kedua-dua tempoh selang antara penerimaan keperluan dan tempoh perkhidmatan. Dalam kes ini, ketumpatan pengedaran tempoh selang antara penerimaan permintaan mempunyai borang

Ketumpatan pengagihan tempoh perkhidmatan:

Aliran permintaan dan perkhidmatan adalah mudah. Biarkan sistem berfungsi dengan kegagalan. QS jenis ini boleh digunakan apabila memodelkan saluran penghantaran dalam rangkaian tempatan. Ia adalah perlu untuk menentukan daya pengeluaran mutlak dan relatif sistem. Mari bayangkan sistem beratur ini dalam bentuk graf (Rajah 2), yang mempunyai dua keadaan:

S 0 - saluran percuma (menunggu);

S 1 - saluran sibuk (permintaan sedang diservis).

Rajah 2. Nyatakan graf bagi QS satu saluran dengan kegagalan

Mari kita nyatakan kebarangkalian keadaan: P 0 (t) - kebarangkalian keadaan "bebas saluran"; P 1 (t) - kebarangkalian keadaan "saluran sibuk". Menggunakan graf keadaan berlabel, kami menyusun sistem persamaan pembezaan Kolmogorov untuk kebarangkalian keadaan:

Sistem persamaan pembezaan linear mempunyai penyelesaian dengan mengambil kira keadaan normalisasi P 0 (t) + P 1 (t) = 1. Penyelesaian sistem ini dipanggil tidak mantap, kerana ia secara langsung bergantung pada t dan kelihatan seperti ini:

P 1 (t) = 1 - P 0 (t) (3.4.3)

Adalah mudah untuk mengesahkan bahawa untuk QS satu saluran dengan kegagalan, kebarangkalian P 0 (t) adalah tidak lebih daripada kapasiti relatif sistem q. Sesungguhnya, P 0 ialah kebarangkalian bahawa pada masa t saluran adalah percuma dan permintaan yang tiba pada masa t akan dilayan, dan, oleh itu, untuk masa tertentu t nisbah purata bilangan permintaan yang disampaikan kepada bilangan yang diterima. juga sama dengan P 0 (t), iaitu q = P 0 (t).

Selepas selang masa yang besar (pada), mod pegun (tetap) dicapai:

Mengetahui daya pengeluaran relatif, mudah untuk mencari yang mutlak. Daya pemprosesan mutlak (A) ialah purata bilangan permintaan yang boleh disediakan oleh sistem baris gilir bagi setiap unit masa:

Kebarangkalian penolakan untuk menyampaikan permintaan akan sama dengan kebarangkalian keadaan "saluran sibuk":

Nilai P terbuka ini boleh ditafsirkan sebagai bahagian purata permohonan yang tidak dilayan dalam kalangan yang diserahkan.

Dalam kebanyakan kes, dalam amalan, sistem baris gilir adalah berbilang saluran, dan, oleh itu, model dengan n saluran penyajian (di mana n>1) tidak diragui minatnya. Proses beratur yang diterangkan oleh model ini dicirikan oleh keamatan aliran input l, manakala tidak lebih daripada n pelanggan (aplikasi) boleh disampaikan secara selari. Tempoh purata perkhidmatan satu permintaan ialah 1/m. Aliran input dan output ialah Poisson. Mod pengendalian saluran servis tertentu tidak menjejaskan mod pengendalian saluran servis lain sistem, dan tempoh prosedur servis bagi setiap saluran ialah pembolehubah rawak tertakluk kepada undang-undang pengedaran eksponen. Matlamat utama menggunakan n saluran perkhidmatan bersambung selari adalah untuk meningkatkan (berbanding dengan sistem saluran tunggal) kelajuan permintaan servis dengan memberi perkhidmatan kepada n pelanggan secara serentak. Graf keadaan sistem baris gilir berbilang saluran dengan kegagalan mempunyai bentuk yang ditunjukkan dalam Rajah 4.

Rajah 4. Nyatakan graf bagi QS berbilang saluran dengan kegagalan

S 0 - semua saluran adalah percuma;

S 1 - satu saluran diduduki, selebihnya percuma;

S k - betul-betul k saluran diduduki, selebihnya adalah percuma;

S n - semua n saluran diduduki, selebihnya adalah percuma.

Persamaan Kolmogorov untuk kebarangkalian keadaan sistem P 0 , ... , P k , ... P n akan mempunyai bentuk berikut:

Syarat awal untuk menyelesaikan sistem ialah:

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0.

Penyelesaian pegun sistem mempunyai bentuk:

Formula untuk mengira kebarangkalian P k (3.5.1) dipanggil formula Erlang.

Mari kita tentukan ciri kebarangkalian fungsi QS berbilang saluran dengan kegagalan dalam mod pegun:

1) kebarangkalian kegagalan:

kerana permintaan ditolak jika ia tiba pada masa semua n saluran sibuk. Nilai P buka mencirikan kesempurnaan servis aliran masuk;

2) kebarangkalian bahawa permintaan akan diterima untuk perkhidmatan (ia juga kapasiti relatif sistem q) melengkapkan P terbuka kepada satu:

3) daya pengeluaran mutlak

4) purata bilangan saluran yang diduduki oleh perkhidmatan () adalah seperti berikut:

Nilai mencirikan tahap pemuatan QS.

Tugasanuntuk pelajaran 2

1. Cawangan komunikasi dengan satu saluran menerima aliran mesej yang paling mudah dengan keamatan l = 0.08 mesej sesaat. Masa penghantaran diedarkan mengikut undang-undang exp. Servis satu mesej berlaku dengan intensiti µ=0.1. Mesej yang tiba pada masa saluran siaran sedang sibuk menghantar mesej yang diterima sebelum ini menerima kegagalan penghantaran.

Coeff. Beban saluran relatif (kebarangkalian penghunian saluran)

P menolak kebarangkalian kegagalan menerima mesej

Q kapasiti relatif cawangan internode

Dan daya pengeluaran mutlak cawangan komunikasi.

2. Cawangan komunikasi mempunyai satu saluran dan menerima mesej setiap 10 saat. Masa perkhidmatan untuk satu mesej ialah 5 saat. Masa penghantaran mesej diedarkan mengikut undang-undang eksponen. Mesej yang tiba semasa saluran sibuk dinafikan perkhidmatan.

takrifkan

Rzan - kebarangkalian penghunian saluran komunikasi (faktor beban relatif)

Q - daya pengeluaran relatif

A - kapasiti mutlak cawangan komunikasi

4. Cawangan internode rangkaian komunikasi sekunder mempunyai n = 4 saluran. Aliran mesej yang tiba untuk penghantaran melalui saluran cawangan komunikasi mempunyai intensiti = 8 mesej sesaat. Purata masa penghantaran satu mesej ialah t = 0.1 saat Mesej yang tiba pada masa semua n saluran sedang sibuk menerima kegagalan penghantaran di sepanjang cawangan komunikasi. Cari ciri-ciri SMO:

PELAJARAN 3

Sistem saluran tunggal dengan siap sedia

Sekarang mari kita pertimbangkan QS satu saluran dengan menunggu. Sistem beratur mempunyai satu saluran. Aliran masuk permintaan perkhidmatan adalah aliran paling mudah dengan intensiti. Keamatan aliran perkhidmatan adalah sama (iaitu, secara purata, saluran yang sentiasa sibuk akan mengeluarkan permintaan yang diservis). Tempoh perkhidmatan adalah pembolehubah rawak tertakluk kepada undang-undang taburan eksponen. Aliran perkhidmatan ialah aliran peristiwa Poisson yang paling mudah. Permintaan yang diterima apabila saluran sibuk akan beratur dan menunggu perkhidmatan. QS ini adalah yang paling biasa dalam pemodelan. Dengan satu darjah atau penghampiran yang lain, ia boleh digunakan untuk mensimulasikan hampir mana-mana nod rangkaian komputer tempatan (LAN).

Mari kita anggap bahawa tidak kira berapa banyak permintaan yang tiba pada input sistem penyajian, sistem ini (baris gilir + pelanggan sedang dilayan) tak boleh menampung lebih daripada keperluan-N (aplikasi), iaitu pelanggan yang tidak ditahan terpaksa dilayan di tempat lain. Sistem M/M/1/N. Akhir sekali, permintaan perkhidmatan penjanaan sumber mempunyai kapasiti tanpa had (besar tak terhingga). Graf keadaan QS dalam kes ini mempunyai bentuk yang ditunjukkan dalam Rajah 3

Rajah 3. Nyatakan graf bagi QS satu saluran dengan menunggu (skim kematian dan pembiakan)

Negeri QS mempunyai tafsiran berikut:

S 0 - "bebas saluran";

S 1 - "saluran sibuk" (tiada baris gilir);

S 2 - "saluran sibuk" (satu permintaan berada dalam baris gilir);

S n - "saluran sibuk" (n -1 aplikasi berada dalam baris gilir);

S N - "saluran sibuk" (N - 1 aplikasi berada dalam baris gilir).

Proses pegun dalam sistem ini akan diterangkan oleh sistem persamaan algebra berikut:

di mana p=faktor beban

n - nombor negeri.

Penyelesaian kepada sistem persamaan di atas untuk model QS kami mempunyai bentuk:

Nilai kebarangkalian awal untuk QS dengan panjang baris gilir terhad

Untuk QS dengan baris gilir tak terhingga Н =? :

P 0 =1- s (3.4.7)

Perlu diingatkan bahawa pemenuhan syarat pegun untuk QS tertentu tidak diperlukan, kerana bilangan permohonan yang diterima masuk ke sistem penyajian dikawal dengan memperkenalkan sekatan pada panjang baris gilir, yang tidak boleh melebihi (N - 1) , dan bukan mengikut nisbah antara keamatan aliran input, iaitu bukan nisbah c = l/m.

Tidak seperti sistem saluran tunggal, yang dianggap di atas dan dengan baris gilir tanpa had, dalam kes ini pengagihan pegun bilangan permintaan wujud untuk sebarang nilai terhingga faktor beban c.

Mari kita tentukan ciri-ciri QS saluran tunggal dengan menunggu dan panjang giliran terhad bersamaan dengan (N - 1) (M/M/1/N), serta untuk QS saluran tunggal dengan penimbal kapasiti tanpa had. (M/M/1/?). Untuk QS dengan baris gilir yang tidak terhingga, syarat dengan<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) kebarangkalian penolakan untuk menyampaikan permohonan:

Salah satu ciri sistem yang paling penting di mana kehilangan permintaan adalah mungkin ialah kebarangkalian kehilangan P bahawa permintaan sewenang-wenangnya akan hilang. Dalam kes ini, kebarangkalian kehilangan permintaan sewenang-wenangnya bertepatan dengan kebarangkalian bahawa pada masa yang sewenang-wenangnya semua tempat menunggu telah diduduki, i.e. formula P daripada k = P N adalah sah

2) kapasiti sistem relatif:

Untuk SMO tanpa hadbarisan ke q =1, kerana semua permintaan akan dilayan

3) daya pengeluaran mutlak:

4) purata bilangan aplikasi dalam sistem:

L S dengan baris gilir tanpa had

5) purata masa aplikasi kekal dalam sistem:

Untuk giliran tanpa had

6) purata tempoh penginapan pelanggan (permohonan) dalam baris gilir:

Dengan giliran tanpa had

7) purata bilangan aplikasi (pelanggan) dalam baris gilir (panjang giliran):

dengan baris gilir tanpa had

Membandingkan ungkapan untuk purata masa menunggu dalam baris gilir T och dan formula untuk purata panjang baris gilir L och, serta purata masa kediaman permintaan dalam sistem T S dan purata bilangan permintaan dalam sistem L S, kita lihat itu

L och =l*T och L s =l* T s

Ambil perhatian bahawa formula ini juga sah untuk banyak sistem baris gilir yang lebih umum daripada sistem M/M/1 yang sedang dipertimbangkan dan dipanggil formula Little. Kepentingan praktikal formula ini ialah ia menghapuskan keperluan untuk mengira secara langsung nilai T och dan T s dengan nilai yang diketahui bagi nilai L och dan L s dan sebaliknya.

Tugas saluran tunggal SMOdengan jangkaan, Denganmenunggu danpanjang giliran terhad

1. Diberi QS satu baris dengan storan baris gilir tanpa had. Permohonan diterima setiap t = 14 saat. Purata masa penghantaran satu mesej ialah t=10 saat. Mesej yang tiba pada masa saluran penyajian sibuk diterima dalam baris gilir tanpa meninggalkannya sebelum servis dimulakan.

Tentukan penunjuk prestasi berikut:

2. Cawangan komunikasi internod, yang mempunyai satu saluran dan storan baris gilir untuk m=3 mesej belum selesai (N-1=m), menerima aliran mesej paling mudah dengan keamatan l=5 mesej. dalam saat. Masa penghantaran mesej diedarkan mengikut undang-undang eksponen. Purata masa penghantaran satu mesej ialah 0.1 saat. Mesej yang tiba pada masa saluran siaran sedang sibuk menghantar mesej yang diterima sebelum ini dan tiada ruang kosong dalam pemacu ditolak.

P terbuka - kebarangkalian kegagalan untuk menerima mesej

Sistem L - purata jumlah bilangan mesej dalam baris gilir dan dihantar sepanjang cawangan komunikasi

T o - purata masa mesej kekal dalam baris gilir sebelum penghantaran bermula

T syst - purata jumlah masa mesej kekal dalam sistem, iaitu jumlah purata masa menunggu dalam baris gilir dan purata masa penghantaran

Q - daya pengeluaran relatif

A - daya pengeluaran mutlak

3. Cawangan internod rangkaian komunikasi sekunder, yang mempunyai satu saluran dan storan baris gilir untuk m = 4 (N-1=4) mesej menunggu, menerima aliran mesej paling mudah dengan intensiti = 8 mesej sesaat. Masa penghantaran mesej diedarkan mengikut undang-undang eksponen. Purata masa penghantaran satu mesej ialah t = 0.1 saat. Mesej yang tiba pada masa saluran penyajian sedang sibuk menghantar mesej yang diterima sebelum ini dan tiada ruang kosong dalam pemacu ditolak oleh baris gilir.

P terbuka - kebarangkalian kegagalan untuk menerima mesej untuk penghantaran melalui saluran komunikasi cawangan internode;

L och - purata bilangan mesej dalam baris gilir ke cawangan komunikasi rangkaian sekunder baris gilir;

Sistem L - jumlah purata jumlah mesej dalam baris gilir dan dihantar sepanjang cawangan komunikasi rangkaian sekunder;

T och - purata masa mesej kekal dalam baris gilir sebelum penghantaran bermula;

R zan - kebarangkalian saluran komunikasi sibuk (pekali beban saluran relatif);

Q ialah kapasiti relatif cawangan internodal;

A ialah kapasiti mutlak cawangan internodal;

4. Cawangan komunikasi internod, yang mempunyai satu saluran dan storan baris gilir untuk m=2 mesej menunggu, menerima aliran mesej paling mudah dengan keamatan l=4 mesej. dalam beberapa saat. Masa penghantaran mesej diedarkan mengikut undang-undang eksponen. Purata masa penghantaran satu mesej ialah 0.1 saat. Mesej yang tiba pada masa saluran siaran sedang sibuk menghantar mesej yang diterima sebelum ini dan tiada ruang kosong dalam pemacu ditolak.

Tentukan penunjuk prestasi berikut bagi cawangan komunikasi:

P terbuka - kebarangkalian kegagalan untuk menerima mesej

L och - purata bilangan mesej dalam baris gilir ke cawangan komunikasi

Sistem L - purata jumlah bilangan mesej dalam baris gilir dan dihantar sepanjang cawangan komunikasi

T o - purata masa mesej kekal dalam baris gilir sebelum penghantaran bermula

T syst - purata jumlah masa mesej kekal dalam sistem, iaitu jumlah purata masa menunggu dalam baris gilir dan purata masa penghantaran

R zan - kebarangkalian penghunian saluran komunikasi (pekali beban saluran relatif c)

Q - daya pengeluaran relatif

A - daya pengeluaran mutlak

5. Cawangan internode rangkaian komunikasi sekunder, yang mempunyai satu saluran dan baris gilir penyimpanan volum tanpa had bagi mesej menunggu, menerima aliran mesej yang paling mudah dengan keamatan l = 0.06 mesej sesaat. Purata masa penghantaran satu mesej ialah t = 10 saat. Mesej yang tiba pada masa saluran komunikasi sibuk diterima dalam baris gilir dan tidak meninggalkannya sehingga perkhidmatan bermula.

Tentukan penunjuk prestasi berikut bagi cawangan komunikasi rangkaian sekunder:

L och - purata bilangan mesej dalam baris gilir ke cawangan komunikasi;

Sistem L - jumlah purata jumlah mesej dalam baris gilir dan dihantar di sepanjang cawangan komunikasi;

T och - purata masa mesej kekal dalam baris gilir;

T syst ialah purata jumlah masa mesej kekal dalam sistem, iaitu jumlah purata masa menunggu dalam baris gilir dan purata masa penghantaran;

R zan - kebarangkalian saluran komunikasi sibuk (faktor beban saluran relatif);

Q - kapasiti relatif cawangan internodal;

A - kapasiti mutlak cawangan internodal

6. Diberi QS satu baris dengan storan baris gilir tanpa had. Permohonan diterima setiap t = 13 saat. Purata masa untuk menghantar satu mesej

t=10 saat. Mesej yang tiba pada masa saluran penyajian sibuk diterima dalam baris gilir tanpa meninggalkannya sebelum servis dimulakan.

Tentukan penunjuk prestasi berikut:

L och - purata bilangan mesej dalam baris gilir

Sistem L - purata jumlah bilangan mesej dalam baris gilir dan dihantar sepanjang cawangan komunikasi

T o - purata masa mesej kekal dalam baris gilir sebelum penghantaran bermula

T syst - purata jumlah masa mesej kekal dalam sistem, iaitu jumlah purata masa menunggu dalam baris gilir dan purata masa penghantaran

Rzan - kebarangkalian penghunian (pekali beban saluran relatif c)

Q - daya pengeluaran relatif

A - daya pengeluaran mutlak

7. Pos diagnostik khusus ialah QS saluran tunggal. Bilangan tempat letak kereta untuk kereta yang menunggu diagnostik adalah terhad dan bersamaan dengan 3 [(N - 1) = 3]. Jika semua tempat letak kereta telah diduduki, iaitu, sudah ada tiga kereta dalam barisan, maka kereta seterusnya yang tiba untuk diagnostik tidak akan diletakkan dalam barisan untuk perkhidmatan. Aliran kereta yang tiba untuk diagnostik diedarkan mengikut undang-undang Poisson dan mempunyai keamatan = 0.85 (kereta sejam). Masa diagnostik kenderaan diagihkan mengikut undang-undang eksponen dan purata 1.05 jam.

Ia diperlukan untuk menentukan ciri kebarangkalian stesen diagnostik yang beroperasi dalam mod pegun: P 0 , P 1 , P 2 , P 3 , P 4 , P buka, q,A, L och, L sys, T och, T sys

PELAJARAN 4

QS berbilang saluran dengan menunggu, dengan menunggu dan panjang giliran terhad

Mari kita pertimbangkan sistem beratur berbilang saluran dengan menunggu. QS jenis ini sering digunakan apabila memodelkan kumpulan terminal pelanggan LAN yang beroperasi dalam mod interaktif. Proses beratur dicirikan oleh yang berikut: aliran input dan output ialah Poisson dengan intensiti dan, masing-masing; Tidak lebih daripada n pelanggan boleh dilayan secara selari. Sistem ini mempunyai n saluran perkhidmatan. Tempoh purata perkhidmatan untuk satu pelanggan ialah 1/m untuk setiap saluran. Sistem ini juga merujuk kepada proses kematian dan pembiakan.

c=l/nm - nisbah keamatan aliran masuk kepada jumlah keamatan perkhidmatan, ialah faktor beban sistem

(Dengan<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

di mana P 0 ialah kebarangkalian keadaan bebas semua saluran dengan baris gilir tanpa had, k ialah bilangan permintaan.

jika kita mengambil c = l / m, maka P 0 boleh ditentukan untuk baris gilir tanpa had:

Untuk baris gilir terhad:

di mana m ialah panjang giliran

Dengan baris gilir tanpa had:

Kapasiti relatif q=1,

Kapasiti mutlak A=l,

Purata bilangan saluran yang diduduki Z=A/m

Dengan giliran terhad

1 Cawangan internode rangkaian komunikasi sekunder mempunyai n = 4 saluran. Aliran mesej yang tiba untuk penghantaran melalui saluran cawangan komunikasi mempunyai intensiti = 8 mesej sesaat. Purata masa t = 0.1 untuk menghantar satu mesej oleh setiap saluran komunikasi ialah t/n = 0.025 saat. Masa menunggu untuk mesej dalam baris gilir adalah tidak terhad. Cari ciri-ciri SMO:

P terbuka - kebarangkalian kegagalan penghantaran mesej;

Q ialah kapasiti relatif cawangan komunikasi;

A ialah daya pengeluaran mutlak cawangan komunikasi;

Z - purata bilangan saluran yang diduduki;

L och - purata bilangan mesej dalam baris gilir;

T = purata masa menunggu;

T syst - purata jumlah masa mesej kekal dalam baris gilir dan penghantaran di sepanjang cawangan komunikasi.

2. Bengkel mekanikal loji dengan tiga tiang (saluran) menjalankan pembaikan mekanisasi kecil. Aliran mekanisme rosak yang tiba di bengkel adalah Poisson dan mempunyai intensiti = 2.5 mekanisme sehari, purata masa pembaikan untuk satu mekanisme diagihkan mengikut undang-undang eksponen dan bersamaan dengan = 0.5 hari. Mari kita anggap bahawa tiada bengkel lain di kilang, dan, oleh itu, barisan mekanisme di hadapan bengkel boleh berkembang hampir tanpa had. Ia diperlukan untuk mengira nilai had berikut bagi ciri-ciri kebarangkalian sistem:

Kebarangkalian keadaan sistem;

Purata bilangan aplikasi dalam baris gilir untuk perkhidmatan;

Purata bilangan aplikasi dalam sistem;

Purata tempoh masa aplikasi kekal dalam baris gilir;

Tempoh purata permohonan tinggal dalam sistem.

3. Cawangan internode rangkaian komunikasi sekunder mempunyai n=3 saluran. Aliran mesej yang tiba untuk penghantaran melalui saluran cawangan komunikasi mempunyai keamatan l = 5 mesej sesaat. Purata masa penghantaran satu mesej ialah t=0.1, t/n=0.033 saat Simpanan baris gilir mesej yang menunggu penghantaran boleh mengandungi sehingga m= 2 mesej. Mesej yang tiba pada masa apabila semua tempat dalam baris gilir diduduki menerima kegagalan penghantaran di sepanjang cawangan komunikasi. Cari ciri-ciri QS: P terbuka - kebarangkalian kegagalan penghantaran mesej, Q - daya hantar relatif, A - pemprosesan mutlak, Z - purata bilangan saluran yang diduduki, L och - purata bilangan mesej dalam baris gilir, T jadi - purata menunggu masa, sistem T - purata jumlah masa mesej kekal dalam baris gilir dan dihantar sepanjang cawangan komunikasi.

PELAJARAN 5

Tertutup QS

Mari kita pertimbangkan model servis armada mesin, yang merupakan model sistem baris gilir tertutup. Sehingga kini, kami hanya mempertimbangkan sistem baris gilir yang keamatan aliran masuk permintaan tidak bergantung pada keadaan sistem. Dalam kes ini, sumber permintaan adalah di luar QS dan menjana aliran permintaan tanpa had. Mari kita pertimbangkan sistem baris gilir yang bergantung pada keadaan sistem, dan sumber keperluan adalah dalaman dan menjana aliran permintaan yang terhad. Sebagai contoh, tempat letak mesin yang terdiri daripada mesin N diservis oleh sepasukan mekanik R (N > R), dan setiap mesin boleh diservis oleh hanya seorang mekanik. Di sini, mesin ialah sumber keperluan (permintaan untuk perkhidmatan), dan mekanik ialah saluran perkhidmatan. Mesin yang rosak, selepas diservis, digunakan untuk tujuan yang dimaksudkan dan menjadi sumber keperluan perkhidmatan yang berpotensi. Jelas sekali, keamatan bergantung pada berapa banyak mesin sedang beroperasi (N - k) dan berapa banyak mesin sedang diservis atau berdiri dalam barisan menunggu servis (k). Dalam model yang sedang dipertimbangkan, kapasiti sumber keperluan harus dianggap terhad. Aliran permintaan masuk datang daripada bilangan mesin operasi yang terhad (N - k), yang secara rawak rosak dan memerlukan penyelenggaraan. Selain itu, setiap mesin dari (N - k) sedang beroperasi. Menghasilkan aliran Poisson keperluan dengan keamatan X tanpa mengira objek lain, jumlah (jumlah) aliran masuk mempunyai keamatan. Permintaan yang memasuki sistem apabila sekurang-kurangnya satu saluran percuma diproses serta-merta. Jika permintaan mendapati semua saluran sibuk melayani permintaan lain, maka ia tidak meninggalkan sistem, tetapi masuk ke dalam baris gilir dan menunggu sehingga salah satu saluran menjadi percuma. Oleh itu, dalam sistem beratur tertutup, aliran masuk keperluan terbentuk daripada yang keluar. Keadaan sistem S k dicirikan oleh jumlah bilangan permintaan yang diservis dan dalam baris gilir sama dengan k. Bagi sistem tertutup yang sedang dipertimbangkan, jelas sekali, k = 0, 1, 2, ... , N. Selain itu, jika sistem berada dalam keadaan S k, maka bilangan objek yang beroperasi adalah sama dengan (N - k) . Jika ialah keamatan aliran permintaan bagi setiap mesin, maka:

Sistem persamaan algebra yang menerangkan operasi QS gelung tertutup dalam mod pegun adalah seperti berikut:

Menyelesaikan sistem ini, kita dapati kebarangkalian keadaan k:

Nilai P 0 ditentukan daripada keadaan menormalkan keputusan yang diperoleh menggunakan formula untuk P k , k = 0, 1, 2, ... , N. Mari kita tentukan ciri kebarangkalian sistem berikut:

Purata bilangan permintaan dalam baris gilir untuk perkhidmatan:

Purata bilangan permintaan dalam sistem (menyaji dan beratur)

purata bilangan mekanik (saluran) "terbiar" kerana kekurangan kerja

Nisbah kemalasan objek yang diservis (mesin) dalam baris gilir

Kadar penggunaan kemudahan (mesin)

Nisbah masa henti saluran perkhidmatan (mekanik)

Purata masa menunggu untuk perkhidmatan (masa menunggu untuk perkhidmatan dalam baris gilir)

Masalah QS tertutup

1. Biarkan dua jurutera dengan produktiviti yang sama diperuntukkan untuk menservis sepuluh komputer peribadi (PC). Aliran kegagalan (kepincangan) satu komputer ialah Poisson dengan intensiti = 0.2. Masa penyelenggaraan PC mematuhi undang-undang eksponen. Purata masa untuk menservis satu PC oleh seorang jurutera ialah: = 1.25 jam. Pilihan organisasi perkhidmatan berikut adalah mungkin:

Kedua-dua jurutera menservis kesemua sepuluh komputer, jadi jika PC gagal, ia diservis oleh salah seorang jurutera percuma, dalam kes ini R = 2, N = 10;

Setiap seorang daripada dua jurutera itu menyelenggara lima PC yang diberikan kepadanya. Dalam kes ini R = 1, N = 5.

Ia adalah perlu untuk memilih pilihan terbaik untuk mengatur penyelenggaraan PC.

Adalah perlu untuk menentukan semua kebarangkalian keadaan P k: P 1 - P 10, dengan mengambil kira bahawa menggunakan keputusan pengiraan P k, kita mengira P 0

PELAJARAN 6

Pengiraan trafik.

Teori teletrafik adalah sebahagian daripada teori beratur. Asas teori teletrafik diletakkan oleh saintis Denmark A.K. Erlang. Karya-karya beliau diterbitkan pada tahun 1909-1928. Mari kita berikan definisi penting yang digunakan dalam teori teletrafik (TT). Istilah "lalu lintas" sepadan dengan istilah "beban telefon". Ini merujuk kepada beban yang dicipta oleh aliran panggilan, permintaan dan mesej yang tiba pada input QS. Jumlah trafik ialah amaun jumlah, selang masa integral yang terlepas oleh satu atau sumber lain semasa sumber ini diduduki semasa tempoh masa yang dianalisis. Satu unit kerja boleh dianggap sebagai pekerjaan kedua sumber. Kadangkala anda boleh membaca tentang kerja sejam, dan kadangkala hanya beberapa saat atau jam. Walau bagaimanapun, pengesyoran ITU memberikan dimensi volum trafik dalam erlango-hours. Untuk memahami maksud unit ukuran sedemikian, kita perlu mempertimbangkan parameter trafik yang lain - intensiti trafik. Dalam kes ini, mereka sering bercakap tentang purata intensiti trafik (beban) pada kumpulan tertentu (set) sumber. Jika pada setiap saat masa t daripada selang tertentu (t 1,t 2) bilangan sumber daripada set tertentu yang diduduki dengan trafik servis adalah sama dengan A(t), maka purata intensiti trafik akan

Nilai keamatan trafik dicirikan sebagai purata bilangan sumber yang diduduki oleh trafik servis pada selang masa tertentu. Unit untuk mengukur keamatan beban ialah satu Erlang (1 Erl, 1 E), i.e. 1 Erlang ialah intensiti trafik yang memerlukan penggunaan penuh satu sumber, atau, dalam erti kata lain, di mana sumber itu melaksanakan kerja bernilai satu pekerjaan kedua dalam satu saat. Dalam kesusasteraan Amerika, kadangkala anda boleh menemui satu lagi unit ukuran yang dipanggil CCS-Centrum (atau seratus) Panggilan Kedua. Nombor CCS menggambarkan masa pendudukan pelayan dalam selang 100 saat setiap jam. Keamatan yang diukur dalam CCS boleh ditukar kepada Erlang menggunakan formula 36CCS=1 Erl.

Trafik yang dijana oleh satu sumber dan dinyatakan dalam jam-pekerjaan adalah sama dengan hasil darab bilangan percubaan panggilan c dalam selang masa tertentu T dan purata tempoh satu percubaan t: y = c t (h-z). Trafik boleh dikira dalam tiga cara berbeza:

1) biarkan bilangan panggilan c sejam ialah 1800, dan tempoh purata sesi t = 3 minit, kemudian Y = 1800 panggilan. /h. 0.05 h = 90 Earl;

2) biarkan tempoh t i semua n pekerjaan keluaran sesuatu berkas ditetapkan pada masa T, maka trafik ditentukan seperti berikut:

3) biarkan bilangan keluaran yang diduduki secara serentak bagi rasuk tertentu dipantau pada selang masa yang sama semasa T berdasarkan hasil pemerhatian, fungsi langkah bagi masa x(t) dibina (Rajah 8).

Rajah 8. Sampel keluaran rasuk yang diduduki serentak

Trafik sepanjang masa T boleh dianggarkan sebagai nilai purata x(t) sepanjang masa itu:

di mana n ialah bilangan sampel keluaran yang diduduki serentak. Nilai Y ialah bilangan purata keluaran rasuk yang diduduki serentak semasa masa T.

Turun naik trafik. Trafik pada rangkaian telefon sekunder turun naik dengan ketara dari semasa ke semasa. Pada hari bekerja, lengkung trafik mempunyai dua atau tiga puncak (Rajah 9).

Rajah 9. Turun naik trafik pada siang hari

Jam dalam hari di mana trafik diperhatikan dalam tempoh masa yang panjang adalah paling ketara dipanggil jam paling sibuk (BHH). Pengetahuan tentang trafik dalam CNN pada asasnya penting, kerana ia menentukan bilangan saluran (talian), jumlah peralatan stesen dan nod. Trafik pada hari yang sama dalam minggu mempunyai variasi bermusim. Jika hari dalam seminggu adalah pra-cuti, maka NNN hari ini adalah lebih tinggi daripada hari selepas cuti. Apabila bilangan perkhidmatan yang disokong oleh rangkaian bertambah, begitu juga trafik. Oleh itu, adalah bermasalah untuk meramalkan dengan keyakinan yang mencukupi berlakunya puncak trafik. Trafik dipantau rapi oleh pentadbiran rangkaian dan organisasi reka bentuk. Peraturan pengukuran trafik telah dibangunkan oleh ITU-T dan digunakan oleh pentadbiran rangkaian nasional untuk memenuhi kualiti keperluan perkhidmatan untuk kedua-dua pelanggan rangkaian mereka dan pelanggan rangkaian lain yang disambungkan kepadanya. Teori teletrafik boleh digunakan untuk pengiraan praktikal kerugian atau isipadu peralatan stesen (nod) hanya jika trafik pegun (stabil secara statistik). Keadaan ini lebih kurang berpuas hati dengan lalu lintas di CHNN. Jumlah beban yang memasuki pertukaran telefon automatik setiap hari mempengaruhi pencegahan dan pembaikan peralatan. Ketidaksamaan beban yang memasuki stesen pada siang hari ditentukan oleh pekali kepekatan

Takrifan NNN yang lebih ketat dibuat seperti berikut. Syor ITU E.500 memerlukan analisis 12 bulan data intensiti, memilih 30 hari paling sibuk, mencari waktu paling sibuk pada hari tersebut dan purata ukuran intensiti sepanjang selang ini. Pengiraan intensiti trafik (beban) ini dipanggil anggaran biasa intensiti trafik dalam CHN atau tahap A. Anggaran yang lebih ketat boleh dipuratakan sepanjang 5 hari tersibuk dalam tempoh 30 hari yang dipilih. Gred ini dipanggil gred meningkat atau gred pada tahap B.

Proses mewujudkan trafik. Seperti yang diketahui oleh setiap pengguna rangkaian telefon, tidak semua percubaan untuk mewujudkan sambungan dengan pelanggan yang dipanggil berjaya. Kadangkala anda perlu membuat beberapa percubaan yang tidak berjaya sebelum sambungan yang diingini diwujudkan.

Rajah 10. Gambar rajah peristiwa apabila mewujudkan hubungan antara pelanggan

Mari kita pertimbangkan kemungkinan peristiwa apabila mensimulasikan penubuhan sambungan antara pelanggan A dan B (Rajah 10). Statistik mengenai panggilan dalam rangkaian telefon adalah seperti berikut: bahagian perbualan yang lengkap ialah 70-50%, bahagian panggilan gagal ialah 30-50%. Sebarang percubaan oleh pelanggan mengambil input QS. Dengan percubaan yang berjaya (apabila perbualan telah berlaku), masa pendudukan peranti pensuisan yang mewujudkan sambungan antara input dan output adalah lebih lama daripada percubaan yang tidak berjaya. Pelanggan boleh mengganggu percubaan untuk mewujudkan sambungan pada bila-bila masa. Percubaan semula mungkin disebabkan oleh sebab berikut:

Nombor telah didail dengan salah;

Andaian ralat dalam rangkaian;

Tahap kesegeraan perbualan;

Percubaan sebelumnya yang gagal;

Mengetahui tabiat pelanggan B;

Ragu tentang mendail nombor dengan betul.

Percubaan semula boleh dibuat bergantung pada keadaan berikut:

Tahap segera;

Penilaian sebab kegagalan;

Menilai kebolehlaksanaan percubaan berulang,

Anggaran selang yang boleh diterima antara percubaan.

Kegagalan untuk mencuba semula mungkin disebabkan oleh tahap segera yang rendah. Terdapat beberapa jenis trafik yang dijana melalui panggilan: Y n masuk (cadangan) dan Y n terlepas Trafik Y n termasuk semua percubaan yang berjaya dan tidak berjaya, trafik Y n, yang merupakan sebahagian daripada Y n, termasuk percubaan yang berjaya dan beberapa percubaan yang tidak berjaya.

Y pr = Y r + Y np,

di mana Y p ialah trafik perbualan (berguna), dan Y np ialah trafik yang dijana oleh percubaan yang tidak berjaya. Kesamaan Y p = Y p hanya mungkin dalam kes yang ideal jika tiada kerugian, ralat dengan memanggil pelanggan dan tiada respons daripada pelanggan yang dipanggil.

Perbezaan antara beban yang masuk dan yang dihantar dalam tempoh masa tertentu ialah beban yang hilang.

Ramalan lalu lintas. Sumber yang terhad membawa kepada keperluan untuk pengembangan stesen dan rangkaian secara beransur-ansur. Pentadbiran rangkaian meramalkan peningkatan trafik semasa fasa pembangunan, dengan mengambil kira bahawa:

Pendapatan ditentukan oleh bahagian trafik yang dihantar Y p, - kos ditentukan oleh kualiti perkhidmatan dengan trafik tertinggi;

Sebilangan besar kerugian (kualiti rendah) berlaku dalam kes yang jarang berlaku dan adalah tipikal untuk penghujung tempoh pembangunan;

Jumlah terbesar trafik terlepas berlaku semasa tempoh apabila hampir tiada kerugian - jika kerugian kurang daripada 10%, maka pelanggan tidak bertindak balas kepada mereka. Apabila merancang pembangunan stesen dan rangkaian, pereka bentuk mesti menjawab persoalan apakah keperluan untuk kualiti penyediaan perkhidmatan (kerugian). Untuk melakukan ini, adalah perlu untuk mengukur kerugian trafik mengikut peraturan yang diterima pakai di negara ini.

Contoh pengukuran lalu lintas.

Mula-mula, mari lihat cara anda boleh memaparkan pengendalian QS yang mempunyai beberapa sumber yang memberi perkhidmatan kepada sesetengah trafik secara serentak. Kami akan membincangkan lebih lanjut tentang sumber seperti pelayan yang melayani aliran aplikasi atau keperluan. Salah satu cara yang paling visual dan kerap digunakan untuk menggambarkan proses permintaan servis oleh sekumpulan pelayan ialah carta Gantt. Rajah ini ialah sistem koordinat segi empat tepat dengan paksi-x menggambarkan masa dan paksi-y menandakan titik diskret sepadan dengan pelayan kolam. Rajah 11 menunjukkan carta Gantt untuk sistem tiga pelayan.

Dalam tiga selang masa pertama (kami mengiranya sebagai kedua), pelayan pertama dan ketiga sibuk, dua saat seterusnya - hanya yang ketiga, kemudian yang kedua berfungsi untuk satu saat, kemudian yang kedua dan yang pertama selama dua saat , dan dua saat terakhir - hanya yang pertama.

Gambar rajah yang dibina membolehkan anda mengira isipadu lalu lintas dan keamatannya. Gambar rajah hanya menggambarkan trafik yang dilayan atau terlepas, kerana ia tidak menyatakan apa-apa tentang sama ada permintaan memasuki sistem yang tidak dapat diservis oleh pelayan.

Jumlah trafik yang dilalui dikira sebagai jumlah panjang semua segmen carta Gantt. Kelantangan dalam 10 saat:

Kami mengaitkan dengan setiap selang masa, diplot sepanjang paksi absis, integer sama dengan bilangan pelayan yang diduduki dalam selang unit ini. Nilai A(t) ini ialah keamatan serta-merta. Untuk contoh kita

A(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Mari kita cari purata intensiti trafik dalam tempoh 10 saat

Oleh itu, purata intensiti trafik yang dilalui oleh sistem tiga pelayan yang sedang dipertimbangkan ialah 1.5 Erl.

Parameter beban asas

Komunikasi telefon digunakan oleh pelbagai kategori pelanggan, yang dicirikan oleh:

bilangan sumber beban - N,

purata bilangan panggilan daripada satu sumber dalam masa tertentu (biasanya NNN) - c,

tempoh purata satu sesi sistem pensuisan apabila menservis satu panggilan ialah t.

Keamatan beban akan menjadi

Mari kenal pasti sumber panggilan yang berbeza. Sebagai contoh,

Purata bilangan panggilan ke CHN daripada satu telefon pejabat;

Purata bilangan panggilan daripada satu telefon pangsapuri individu; acara rawak perkhidmatan massa teletrafik

dengan kiraan - sama dari radas untuk kegunaan kolektif;

dengan ma - sama dari satu mesin syiling;

dengan sl - sama dari satu talian penghubung.

Kemudian purata bilangan panggilan daripada satu sumber:

Terdapat data anggaran untuk purata bilangan panggilan daripada satu sumber kategori yang sepadan:

3.5 - 5, =0.5 - 1, dengan kiraan = 1.5 - 2, dengan ma =15 - 30, dengan sl =10 - 30.

Terdapat jenis sambungan berikut, yang, bergantung pada hasil sambungan, menghasilkan beban telefon yang berbeza di stesen:

k р - pekali menunjukkan perkadaran sambungan yang berakhir dengan perbualan;

k з - sambungan yang tidak berakhir dalam perbualan kerana kesibukan pelanggan yang dipanggil;

k tetapi - pekali yang menyatakan perkadaran sambungan yang tidak berakhir dalam perbualan disebabkan oleh tidak membalas pelanggan yang dipanggil;

k osh - sambungan yang tidak berakhir dalam perbualan kerana kesilapan oleh pemanggil;

k mereka - panggilan yang tidak berakhir dengan perbualan atas sebab teknikal.

Semasa operasi rangkaian biasa, nilai pekali ini adalah sama dengan:

k p =0.60-0.75; k z =0.12-0.15; k tetapi =0.08-0.12; k osh =0.02-0.05; k mereka =0.005-0.01.

Tempoh purata sesi bergantung pada jenis sambungan. Contohnya, jika sambungan ditamatkan dengan perbualan, purata tempoh penggunaan peranti t keadaan akan sama dengan

di manakah tempoh penubuhan sambungan;

t comp. - perbualan yang berlaku;

t dalam - tempoh menghantar panggilan ke telefon pelanggan yang dipanggil;

t r - tempoh perbualan

di mana t co ialah isyarat jawapan stesen;

1.5n - masa untuk mendail nombor pelanggan yang dipanggil (n - bilangan aksara dalam nombor);

t s ialah masa yang diperlukan untuk mewujudkan sambungan dengan menukar mekanisme dan memutuskan sambungan selepas tamat perbualan. Nilai anggaran kuantiti yang dipertimbangkan:

t co = 3 saat, t c = 1-2.5 saat, t b = 8-10 saat, t p = 90-130 saat.

Panggilan yang tidak berakhir dalam perbualan juga mewujudkan beban telefon.

Purata masa untuk menduduki peranti apabila pelanggan yang dipanggil sibuk ialah

di mana t sambungan pemasangan ditentukan oleh (4.2.3)

t зз - masa mendengar buzzer sibuk, t зз =6 saat.

Tempoh purata penggunaan peranti apabila pelanggan yang dipanggil tidak menjawab ialah

di mana t pv - masa mendengar isyarat ringback, t pv = 20 saat.

Jika tiada perbualan kerana ralat pelanggan, maka secara purata t osh = 30 saat.

Tempoh kelas yang tidak berakhir dengan perbualan atas sebab teknikal tidak ditentukan, kerana peratusan kelas tersebut adalah kecil.

Daripada semua perkara di atas, ia menunjukkan bahawa jumlah beban yang dicipta oleh sekumpulan sumber di belakang CNN adalah sama dengan jumlah beban jenis aktiviti individu.

di manakah pekali yang mengambil kira terma sebagai saham

Pada rangkaian telefon dengan penomboran tujuh digit, pertukaran telefon automatik telah direka bentuk, komposisi struktur pelanggan adalah seperti berikut:

N akaun = 4000, N ind = 1000, N kiraan = 2000, N ma = 400, N sl = 400.

Purata bilangan panggilan yang diterima daripada satu sumber dalam CHNN adalah sama dengan

Menggunakan formula (4.2.3) dan (4.2.6) kita mencari beban

1.10.62826767 saat z = 785.2 hz.

Purata tempoh pelajaran t daripada formula Y=Nct

t= Y/Nc= 2826767/7800*3.8=95.4 saat.

Muatkan tugas

1. Pada rangkaian telefon dengan penomboran tujuh digit, pertukaran telefon automatik direka bentuk, komposisi struktur pelanggannya adalah seperti berikut:

N uchr =5000, Nind=1500, N kiraan =3000, N ma =500, N sl =500.

Tentukan beban yang tiba di stesen - Y, purata tempoh pekerjaan t, jika diketahui bahawa

dengan ind =4, dengan ind =1, dengan kiraan =2, dengan ma =10, dengan sl =12, t r =120 saat, t dalam =10 saat, k r =0.6, t s =1 saat, =1.1 .

Disiarkan di Allbest.ru

Dokumen yang serupa

Konsep pembolehubah rawak teragih seragam. Kaedah kongruen darab. Pemodelan pembolehubah rawak berterusan dan taburan diskret. Algoritma untuk simulasi hubungan ekonomi antara pemberi pinjaman dan peminjam.

kerja kursus, ditambah 01/03/2011


Konsep umum teori beratur. Ciri-ciri pemodelan sistem beratur. Nyatakan graf sistem QS, persamaan yang menerangkannya. Ciri umum jenis model. Analisis sistem beratur pasar raya.

kerja kursus, ditambah 17/11/2009


Elemen teori beratur. Pemodelan matematik sistem beratur, klasifikasinya. Pemodelan simulasi sistem beratur. Aplikasi praktikal teori, menyelesaikan masalah menggunakan kaedah matematik.

kerja kursus, ditambah 05/04/2011


Konsep proses rawak. Masalah teori beratur. Klasifikasi sistem beratur (QS). Model matematik kebarangkalian. Pengaruh faktor rawak terhadap kelakuan sesuatu objek. QS saluran tunggal dan berbilang saluran dengan menunggu.

kerja kursus, ditambah 25/09/2014


Kajian tentang aspek teori pembinaan dan pengendalian sistem beratur yang berkesan, elemen utamanya, klasifikasi, ciri dan kecekapan operasi. Memodelkan sistem beratur menggunakan bahasa GPSS.

kerja kursus, ditambah 09/24/2010


Pembangunan teori pengaturcaraan dinamik, perancangan rangkaian dan pengurusan pembuatan produk. Komponen teori permainan dalam masalah pemodelan proses ekonomi. Elemen aplikasi praktikal teori beratur.

kerja amali, tambah 01/08/2011


Konsep asas tentang peristiwa rawak, kuantiti dan fungsi. Ciri berangka pembolehubah rawak. Jenis asimetri pengedaran. Penilaian statistik taburan pembolehubah rawak. Menyelesaikan masalah pengenalan struktur-parametrik.

kerja kursus, ditambah 03/06/2012


Memodelkan proses beratur. Pelbagai saluran beratur. Penyelesaian model baris gilir satu saluran dengan kegagalan. Ketumpatan pengagihan tempoh perkhidmatan. Penentuan daya pengeluaran mutlak.

ujian, ditambah 03/15/2016


Ciri-ciri fungsi sistem beratur dalam bidang pengangkutan jalan, struktur dan elemen utamanya. Penunjuk kuantitatif kualiti berfungsi sistem beratur, susunan dan peringkat utama penentuannya.

kerja makmal, tambah 03/11/2011


Menetapkan matlamat pemodelan. Pengenalpastian objek sebenar. Memilih jenis model dan skema matematik. Pembinaan model stokastik berterusan. Konsep asas teori beratur. Tentukan aliran peristiwa. Menyediakan algoritma.