Die Eigenschaften von Grad: Wortlaut, Beweise, Beispiele. Entwicklung der Lektion "Grad mit einem natürlichen Indikator", der die Ziele der Lektion einstellt
Wir haben zuvor darüber gesprochen, was der Grad des Datums ist. Es verfügt über bestimmte Eigenschaften, die zur Lösung von Aufgaben nützlich sind: Sie sind und alle möglichen Indikatoren des Studiums werden in diesem Artikel analysieren. Wir werden auch eindeutig auf den Beispielen zeigen, wie Sie sich in der Praxis erweisen und korrekt anwenden können.
Wir erinnern uns an das Konzept des Grads mit einem natürlichen Indikator, der von uns bereits formuliert ist: Dies ist ein Produkt einer N-Zahl-Anzahl von Multiplizierern, von denen jeder gleich a ist. Wir müssen uns auch daran erinnern, wie man die tatsächlichen Zahlen ordnungsgemäß multipliziert. All dies hilft uns, die folgenden Eigenschaften in dem Umfang mit einem natürlichen Indikator zu formulieren:
Definition 1.
1. Die Haupteigenschaft des Grades: A m · a n \u003d a m + n
Es kann verallgemeinert werden, um: a n 1 · a n 2 · ... · a n k \u003d a n 1 + n 2 + ... + n k.
2. Privateigentum für Grad mit den gleichen Basen: A M: A n \u003d A M - N
3. Eigentum des Arbeitsgrades: (a · b) n \u003d a n · b n
Gleichheit kann erweitert werden: (1 · a 2 · ... · a k) n \u003d a 1 n · a 2 n · ... · a k n
4. Privateigentum in natürlichem Umfang: (A: B) n \u003d a n: b n
5. Wir sind in Grad: (a m) n \u003d a m · n,
Kann verallgemeinert werden, um: ((((((a n 1) n 2) ...) n k \u003d a n 1 · n 2 · ... · n k
6. Vergleichen Sie einen Grad mit Null:
- wenn A\u003e 0, dann mit einem beliebigen natur n, einem n länger als null ist;
- bei A, gleich 0, ist ein N auch Null;
- mit einer.< 0 и таком показателе степени, который будет четным числом 2 · m , a 2 · m будет больше нуля;
- mit einer.< 0 и таком показателе степени, который будет нечетным числом 2 · m − 1 , a 2 · m − 1 будет меньше нуля.
7. Gleichheit a n< b n будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.
8. Ungleichheit A m\u003e a n ist korrekt, sofern M und N natürliche Zahlen sind, M ist größer als n und mehr Null und nicht weniger als eins.
Infolgedessen erhielten wir mehrere Gleichungen; Wenn Sie alle oben genannten Bedingungen beobachten, sind sie identisch. Für jedes der Equals, zum Beispiel für die Haupteigenschaft, können Sie den rechten und linken Teil ändern: a m · a n \u003d a m + n ist derselbe wie ein m + n \u003d a m · a n. In dieser Form wird es häufig zur Vereinfachung der Ausdrücke verwendet.
1. Beginnen wir mit der Grundeigentümer des Grads: Die Gleichheit A m · a n \u003d a m + n ist mit jedem natürlichen M und N und gültig a korrekt. Wie beweisen Sie diese Aussage?
Die Hauptdefinition von Grad mit natürlichen Indikatoren ermöglicht es uns, Gleichheit in das Werk der Multiplizierer umzuwandeln. Wir erhalten einen Datensatz dieses Typs:
Es kann auf reduziert werden ![]() (Erinnern Sie sich an die grundlegenden Eigenschaften der Multiplikation). Infolgedessen erhielten wir den Grad der Anzahl A mit einem natürlichen Indikator M + N. Somit ist ein M + N, das bedeutet, dass die Haupteigenschaft des Grades bedeutet.
(Erinnern Sie sich an die grundlegenden Eigenschaften der Multiplikation). Infolgedessen erhielten wir den Grad der Anzahl A mit einem natürlichen Indikator M + N. Somit ist ein M + N, das bedeutet, dass die Haupteigenschaft des Grades bedeutet.
Wir werden ein bestimmtes Beispiel analysieren, das dies bestätigt.
Beispiel 1.
Also haben wir zwei Grad mit der Basis 2. Ihre natürlichen Indikatoren sind 2 bzw. 3. Wir hatten Gleichheit: 2 2 · 2 3 \u003d 2 2 + 3 \u003d 2 5 Berechnen Sie die Werte, um die Loyalität dieser Gleichheit zu überprüfen.
Führen Sie die notwendigen mathematischen Aktionen aus: 2 2 · 2 3 \u003d (2 · 2) · (2 \u200b\u200b· 2 · 2) \u003d 4 · 8 \u003d 32 und 2 5 \u003d 2 · 2 · 2 · 2 · 2 \u003d 32
Infolgedessen kamen wir heraus: 2 2 · 2 3 \u003d 2 5. Eigentum wird bewiesen.
Aufgrund der Multiplikationseigenschaften können wir eine Verallgemeinerung der Eigenschaft zusammenstellen, die sie in Form von drei und mehr Grad formulieren, in denen Indikatoren natürliche Zahlen sind, und die Basen sind gleich. Wenn Sie die Menge der natürlichen Zahlen n 1, n 2 usw. festlegen, geben wir den Buchstaben K.
a n 1 · a n 2 · ... · a n k \u003d a n 1 + n 2 + ... + n k.
Beispiel 2.
2. Als nächstes müssen wir das folgende Eigentum beweisen, das als Eigentum von Privat- und Inhärenten mit den gleichen Basen bezeichnet wird: Dies ist die Gleichheit AM: AN \u003d AM - N, das für jeden natürlichen M und n (mit m gültig ist) größer n)) und andere von null gültig.
Zunächst einmal erklären, was die Bedeutung der im Wortlaut genannten Bedingungen ist. Wenn wir ein Null nehmen, dann finden wir infolgedessen eine Abteilung für Null, die nicht möglich ist (weil 0 n \u003d 0). In der Bedingung, dass die Zahl M notwendigerweise mehr n hatte, ist es notwendig, dass wir im Rahmen natürlicher Indikatoren des Grades widerstehen können: n von m abziehen, wir bekommen eine natürliche Zahl. Wenn der Zustand nicht respektiert ist, haben wir eine negative Zahl oder Null, und wir werden erneut über das Studium von Grad mit natürlichen Indikatoren hinausgehen.
Jetzt können wir zum Beweis gehen. Von den zuvor untersuchten, erinnern wir uns an die grundlegenden Eigenschaften von Fraktionen und formulieren Gleichheit wie folgt:
ein m-n · a n \u003d a (m - n) + n \u003d a m
Daraus kann abgeleitet werden: ein m-n · a n \u003d a m
Erinnern Sie sich an die Beziehung zwischen Division und Multiplikation. Daraus folgt, dass ein M - n privater Abschlüsse ein M und ein N ist. Dies ist der Nachweis der zweiten Eigenschaft des Grades.
Beispiel 3.
Wir werden spezifische Zahlen für die Klarheit in den Indikatoren ersetzen, und die Grundlage des Grads ist mit π: π 5: π 2 \u003d π 5 - 3 \u003d π 3 bezeichnet
3. Im Folgenden werden wir den Grad der Arbeit analysieren: (a · b) n \u003d a n · b n mit einem beliebigen gültigen A und B und natürlichem N.
Nach der grundlegenden Bestimmung des Grades mit einem natürlichen Indikator können wir die gleiche Gleichheit formulieren:

Erinnern Sie sich an die Multiplikationseigenschaften, schreiben Sie:  . Dies bedeutet das gleiche wie ein N · B N.
. Dies bedeutet das gleiche wie ein N · B N.
Beispiel 4.
2 3 · - 4 2 5 4 \u003d 2 3 4 · - 4 2 5 4
Wenn es drei und mehr Multiplikatoren gibt, erstreckt sich diese Eigenschaft auch auf diesen Fall. Wir stellen die Bezeichnung k für die Anzahl der Multiplikatoren vor und schreiben:
(A 1 · a 2 · ... · a k) n \u003d a 1 n · a 2 n · ... · a k n
Beispiel 5
Mit bestimmten Zahlen erhalten wir folgende treue Gleichheit: (2 · (- 2, 3) · a) 7 \u003d 2 7 · (- 2, 3) 7 · a
4. Danach werden wir versuchen, das Eigentum des Privates zu beweisen: (a: b) n \u003d a n: b n mit einem echten A und B, wenn B nicht 0 ist, und n ist eine natürliche Zahl.
Um zu beweisen, können Sie das bisherige Grad-Eigenschaft verwenden. If (a: b) n · bn \u003d ((a: b) · b) n \u003d a, a (a: b) n · bn \u003d ein, dann stellt sich heraus, dass (A: b) n privat ist, wenn es privat ist ein auf BN.
Beispiel 6.
Berechnen Sie Beispiel: 3 1 2: - 0. 5 3 \u003d 3 1 2 3: (- 0, 5) 3
Beispiel 7.
Beginnen wir gleich aus dem Beispiel: (5 2) 3 \u003d 5 2 · 3 \u003d 5 6
Und jetzt formulieren wir die Gleichheitskette, die die Treue der Gleichheit beweisen: 
Wenn wir im Beispiel haben, gibt es Grad-Grad, dann ist diese Eigenschaft auch für sie fair. Wenn wir natürliche Zahlen p, q, r, s haben, dann ist es wahr:
a p y s \u003d a p · · · · s
Beispiel 8.
Besonderheiten hinzufügen: ((((((5, 2) 3) 2) 5 \u003d (5, 2) 3 · 2 · 5 \u003d (5, 2) 30
6. Eine andere Eigenschaft von Grade mit einer natürlichen Zahl, die wir beweisen müssen, ist die Vergleichseigenschaft.
Mit dem vergleichbaren Grad mit Null beginnen. Warum ein n\u003e 0, sofern und mehr als 0?
Wenn Sie eine positive Zahl zu einem anderen multiplizieren, erhalten wir auch eine positive Zahl. Wenn Sie diese Tatsache kennen, können wir sagen, dass es nicht von der Anzahl der Multiplikatoren abhängt - das Ergebnis der Multiplikation einer beliebigen Anzahl von positiven Zahlen ist die Zahl positiv. Und wie ist der Grad wie nicht das Ergebnis der Multipliziernummern? Dann ist es für jeden Grad A n mit positiver Basis und der natürlichen Indikator wahr.
Beispiel 9.
3 5\u003e 0, (0, 00201) 2\u003e 0 und 34 9 13 51\u003e 0
Es ist auch offensichtlich, dass der Grad mit der Basis gleich Null, sich selbst null ist. In welchem \u200b\u200bMaße haben wir nicht Null gebaut, er wird bleiben.
Beispiel 10.
0 3 \u003d 0 und 0 762 \u003d 0
Wenn die Grundlage des Grads eine negative Zahl ist, ist die Beweise hier etwas komplizierter, da das Konzept der Parität / Seltsamkeit des Indikators wichtig wird. Nehmen Sie, um mit dem Fall zu beginnen, wenn die Figur sogar ist, und wir bezeichnen es 2 · m, wo M eine natürliche Zahl ist.

Erinnern Sie sich, wie korrekt multipliziert negative Zahlen multipliziert: Die Arbeit A · A ist gleich dem Produkt der Module, und daher ist es eine positive Zahl. Dann  Und der Grad A 2 · m ist ebenfalls positiv.
Und der Grad A 2 · m ist ebenfalls positiv.
Beispiel 11.
Zum Beispiel (- 6) 4\u003e 0, (- 2, 2) 12\u003e 0 und - 2 9 6\u003e 0
Und wenn der Indikator des Grads mit einer negativen Base eine ungerade Zahl ist? Bezeichnen es 2 · m - 1.
Dann 
Alle Werke · A, nach den Eigenschaften der Multiplikation, sind auch positiv, ihre Arbeit. Wenn wir es jedoch an die einzige verbleibende Zahl A multiplizieren, ist das Endergebnis negativ.
Dann erhalten wir: (- 5) 3< 0 , (− 0 , 003) 17 < 0 и - 1 1 102 9 < 0
Wie beweist man es?
eIN.< b n – неравенство, представляющее собой произведение левых и правых частей nверных неравенств a < b . Вспомним основные свойства неравенств справедливо и a n < b n .
Beispiel 12.
Zum Beispiel treue Ungleichheiten: 3 7< (2 , 2) 7 и 3 5 11 124 > (0 , 75) 124
8. Wir haben die letzte Immobilie beweisen: Wenn wir zwei Grad haben, deren Grundlagen derselbe und positiv sind, und die Indikatoren sind natürliche Zahlen, dann ist das von ihnen mehr, der Indikator ist geringer als; Und von zwei Grad mit natürlichen Indikatoren und den gleichen Basen, große Einheiten, mehr als der Grad, deren Indikator größer ist.
Wir beweisen diese Anschuldigungen.
Um zu beginnen, müssen wir sicherstellen, dass ein m< a n при условии, что m больше, чем n , и а больше 0 , но меньше 1 .Теперь сравним с нулем разность a m − a n
Ich achle ein N für Klammern ein, woraufhin unser Unterschied das Formular a n · (a m - n - 1) nimmt. Das Ergebnis ist negativ (da das Ergebnis einer Multiplikation einer positiven Zahl negativ ist). In der Tat ist gemäß den anfänglichen Bedingungen M - N\u003e 0, dann ein M-N-1 negativ, und der erste Faktor ist positiv, sowie ein natürlicher Grad mit positiver Basis.
Wir kamen heraus, dass ein M - A n< 0 и a m < a n . Свойство доказано.
Es bleibt, den Nachweis des zweiten Teils der oben formulierten Genehmigung zu führen: ein m\u003e a gilt für m\u003e n und a\u003e 1. Wir zeigen den Unterschied an und fassen die N für Klammern zusammen: (ein M - N - 1). Schiff a n mit A, größeren Einheiten, ergibt ein positives Ergebnis; Und der Unterschied selbst wird aufgrund der Anfangsbedingungen auch positiv sein, und an einem Einheit in\u003e 1 Grad A m - n mehr Einheiten. Es stellt sich heraus, ein M - A n\u003e 0 und ein m\u003e a n, das wir beweisen mussten.
Beispiel 13.
Beispiel mit bestimmten Zahlen: 3 7\u003e 3 2
Die wichtigsten Eigenschaften von Grad mit ganzzahligen Indikatoren
Für Grad mit integeren positiven Indikatoren sind Eigenschaften ähnlich, da ganze positive Zahlen natürlich sind, und daher ist alle oben genannten Gleichheit für sie gültig. Sie eignen sich auch für Fälle, wenn Indikatoren negativ oder gleich Null sind (vorausgesetzt, dass die Basis der Grad des ungleichmäßigen Grades ist).
Somit sind die Eigenschaften von Grad für alle Basen A und B gleich (vorausgesetzt, diese Zahlen sind gültig und nicht gleich 0) und beliebige Indikatoren M und N (vorausgesetzt, sie sind intenger). Wir schreiben sie kurz als Formeln:
Definition 2.
1. ein m · a n \u003d a m + n
2. A m: a n \u003d a m - n
3. (a · b) n \u003d a n · b n
4. (A: b) n \u003d a n: b n
5. (a m) n \u003d a m · n
6. A N.< b n и a − n > B - n unter dem Zustand eines ganzen positiven n, positiven a und b, a< b
7 UHR MORGENS.< a n , при условии целых m и n , m > N und 0.< a < 1 , при a > 1 a m\u003e a n.
Wenn die Basis des Grads Null ist, dann machen die Aufzeichnungen A M und A N nur im Fall von natürlichem und positivem M und N sinnvoll. Infolgedessen erhalten wir, dass das Wortlaut höher ist und bei Fällen mit einem Grad mit Nullbasis, wenn alle anderen Bedingungen beobachtet werden.
Die Beweise dieser Eigenschaften in diesem Fall sind unkompliziert. Wir müssen uns daran erinnern, was ein Abschluss mit einer natürlichen und intenregion, sowie die Eigenschaften von Aktionen mit gültigen Nummern.
Wir werden das Grad-Anwesen in den Grad analysieren und beweisen, dass es für das gesamte Positive und für unentschiedene angemessene Zahlen trifft. Beginnen wir mit dem Nachweis von Gleichungen (AP) q \u003d AP · q, (A - P) q \u003d a (- p) · q, (AP) - q \u003d · · · (- q) und (a - p) - Q \u003d a (- p) · (- q)
Bedingungen: p \u003d 0 oder natürliche Zahl; Q - in ähnlicher Weise.
Wenn die Werte P und Q größer als 0 sind, dann gelang es uns (a p) q \u003d a p · q. Wir haben bereits eine ähnliche Gleichheit erwiesen. Wenn p \u003d 0, dann:
(A 0) q \u003d 1 q \u003d 1 A 0 · q \u003d A 0 \u003d 1
Daher (A 0) q \u003d A 0 · q
Für q \u003d 0 ist alles gleich:
(A p) 0 \u003d 1 a p · 0 \u003d a 0 \u003d 1
Ergebnis: (a p) 0 \u003d a p · 0.
Wenn beide Indikatoren Null sind, dann (A 0) 0 \u003d 1 0 \u003d 1 und A 0 · 0 \u003d A 0 \u003d 1 bedeutet es (A 0) 0 \u003d A 0 · 0.
Erinnern Sie sich an die bewährte Eigenschaft des Privatlands in das Land und notieren Sie sich an:
1 a p q \u003d 1 q a p q
Wenn 1 p \u003d 1 · 1 · ... · 1 \u003d 1 und a p q \u003d a p · q, dann 1 q a p q \u003d 1 a p · q
Wir können diesen Eintrag aufgrund der grundlegenden Multiplikationsregeln in A (- P) · Q konvertieren.
Nur: ein p-q \u003d 1 (a p) q \u003d 1 a p · q \u003d a - (p · q) \u003d a p · (- q).
Und (a - p) - q \u003d 1 a p - q \u003d (a p) q \u003d a p · q \u003d a (- p) · (- q)
Die verbleibenden Eigenschaften des Grades können auf ähnliche Weise nachgewiesen werden, um vorhandene Ungleichheiten umzuwandeln. Wir wohnen nicht detailliert, wir geben nur komplexe Momente an.
Nachweis der vorletzten Eigenschaft: RECALL, A - N\u003e B - N trifft auf alle negativen Werte eines beliebigen positiven A und B zu, vorausgesetzt, dass weniger b.
Dann kann die Ungleichung wie folgt umgewandelt werden:
1 a n\u003e 1bn
Wir schreiben die rechten und linken Teile in Form eines Unterschieds und führen die erforderlichen Transformationen aus:
1 a n - 1 b n \u003d b n - a n a n · b n
Erinnern daran, dass in der Bedingung weniger als B, dann gemäß der Bestimmung des Grades mit einer natürlichen Figur: - a n< b n , в итоге: b n − a n > 0 .
ein N · Bn ergibt letztendlich eine positive Zahl, da seine Multiplizierer positiv sind. Infolgedessen haben wir eine Fraktion B N - a n a n · bn, die letztendlich auch ein positives Ergebnis ergibt. Daher 1 a n\u003e 1 b n von a - n\u003e b - n, den wir beweisen mussten.
Die letzte Eigenschaft von Grade mit ganzzahligen Indikatoren wird dem Anwesen von Grad mit natürlichen Indikatoren erwiesen.
Die wichtigsten Eigenschaften von Grad mit rationalen Indikatoren
In den früheren Artikeln werden wir demontiert, was ein Abschluss mit einem rationalen (fraktionalen) Indikator ist. Ihre Eigenschaften sind die gleichen wie Grad mit Integer-Indikatoren. Wir schreiben:
Definition 3.
1. AM 1 N 1 · AM 2 N 2 \u003d AM 1 N 1 + M 2 N 2 an A\u003e 0, und wenn M 1 N 1\u003e 0 und M 2 N 2\u003e 0, dann bei einem ≥ 0 (Produkteigenschaft Grad mit den gleichen Basen).
2. A M 1 N 1: B M 2 N 2 \u003d A M 1 N 1 - M 2 N 2, falls A\u003e 0 (Privateigentum).
3. A · BMN \u003d AMN · BMN an einem\u003e 0 und b\u003e 0, und wenn m 1 n 1\u003e 0 und m 2 n 2\u003e 0, dann an einem ≥ 0 und (oder) b ≥ 0 (die Eigenschaft von die Arbeit im fraktionalen Grad).
4. A: B M N \u003d A M N: B M N mit A\u003e 0 und B\u003e 0, und wenn M n\u003e 0, dann an einem ≥ 0 und b\u003e 0 (Eigenschaft des privaten Grades).
5. AM 1 N 1 M 2 N 2 \u003d AM 1 N 1 · M 2 N 2 an A\u003e 0, und wenn M 1 N 1\u003e 0 und M 2 N 2\u003e 0, dann bei einem ≥ 0 (Grad in Grad in Grad).
6. A P.< b p при условии любых положительных a и b , a < b и рациональном p при p > 0; Wenn P.< 0 - a p > B p (ein Vergleich von Grade mit gleichen rationalen Indikatoren).
7. A P.< a q при условии рациональных чисел p и q , p > Q bei 0.< a < 1 ; если a > 0 - A p\u003e a q
Um diese Bestimmungen zu beweisen, müssen wir uns daran erinnern, dass eine solche Bruchrate die Eigenschaften der Arithmetikwurzel des N-Grades und die Eigenschaften des Grades mit dem Integer-Indikator sind. Wir werden jede Eigenschaft analysieren.
Je nach der Tatsache, dass es sich um einen Abschluss mit einem fraktionalen Indikator handelt, erhalten wir:
a M 1 N 1 \u003d A M 1 N 1 und A M 2 N 2 \u003d A M 2 N 2, daher ein M 1 N 1 · A M 2 N 2 \u003d A M 1 N 1 · A M 2 N 2
Die Eigenschaften der Wurzel ermöglichen es uns, Gleichheit zurückzuziehen:
a M 1 · M 2 N 1 · N 2 · A M 2 · M 1 N 2 · N 1 \u003d A M 1 · N 2 · A M 2 · N 1 N 1 · N 2
Daraus erzielen wir: ein M 1 · N 2 · A M 2 · N 1 N 1 · N 2 \u003d A M 1 · N 2 + M 2 · N 1 N 1 · N 2
Wir transformieren:
ein M 1 · N 2 · A M 2 · N 1 N 1 · N 2 \u003d A M 1 · N 2 + M 2 · N 1 N 1 · N 2
Der Indikator kann in das Formular geschrieben werden:
m 1 · N 2 + M 2 · N 1 N 1 · N 2 \u003d M 1 · N 2 N 1 · N 2 + M 2 · N 1 N 1 · N 2 \u003d M 1 N 1 + M 2 N 2
Dies ist ein Beweis. Die zweite Immobilie ist absolut gleich erwiesen. Wir schreiben die Kette der Gleichungen:
aM 1 N 1: AM 2 N 2 \u003d AM 1 N 1: AM 2 N 2 \u003d AM 1 · N 2: AM 2 · N 1 N 1 · N 2 \u003d AM 1 · N 2 - M 2 · N 1 N 1 · N 2 \u003d AM 1 · N 2 - M 2 · N 1 N 1 · N 2 \u003d AM 1 · N 2 N 1 · N 2 - M 2 · N 1 N 1 · N 2 \u003d AM 1 N 1 - M 2 N 2.
Beweise für andere Gleichungen:
a · bm n \u003d (a · b) m n \u003d a m · b m n \u003d a m n · b m n \u003d a m n · b m n; (A: b) m n \u003d (A: b) m n \u003d a m: b m n \u003d \u003d a m n: b m n \u003d a m n: b m n; AM 1 N 1 M 2 N 2 \u003d AM 1 N 1 M 2 N 2 \u003d AM 1 N 1 M 2 N 2 \u003d AM 1 M 2 N 1 N 2 \u003d AM 1 · M 2 N 1 N 2 \u003d AM 1 · m 2 N 2 · N 1 \u003d AM 1 · M 2 N 2 · N 1 \u003d AM 1 N 1 · M 2 N 2
Nächste Eigenschaft: Lassen Sie uns das nachweisen, dass für alle Werte A und B größer als 0, falls und weniger B, ein P< b p , а для p больше 0 - a p > B S.
Stellen Sie sich eine rationale Zahl P als m n vor. In diesem Fall ist der M eine Zahl, N -Net. Dann Bedingungen P.< 0 и p > 0 wird sich auf m ausbreiten< 0 и m > 0. Bei m\u003e 0 und a< b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство a m < b m .
Wir verwenden die Eigenschaften der Wurzeln und bringen: a m n< b m n
Berücksichtigung der Positivität der Werte von A und B, umschreiben Sie die Ungleichheit als m n< b m n . Оно эквивалентно a p < b p .
Auf dieselbe Weise bei m< 0 имеем a a m > B M, wir erhalten ein M n\u003e b m n bedeutet ein mn n\u003e b m n und a p\u003e b p.
Wir haben den Nachweis der letzten Immobilie mitbringen. Wir beweisen das für rationale Zahlen p und q, p\u003e q um 0< a < 1 a p < a q , а при a > 0 ist wahr, ein p\u003e a q.
Die rationale Zahlen p und q können zu einem gemeinsamen Nenner führen und Fraktionen m 1 N und M 2 N erhalten
Hier sind M 1 und M 2 Ganzzahlen und n - natürlich. Wenn p\u003e q, dann m 1\u003e m2 (angesichts der Fraktionsvergleichsregel). Dann um 0.< a < 1 будет верно a m 1 < a m 2 , а при a > 1 - Ungleichung a 1 m\u003e a 2 m.
Sie können in folgendem Formular neu geschrieben werden:
ein m 1 n< a m 2 n a m 1 n > Ein m 2 n
Dann können Sie die Umwandlung und am Ende machen:
ein m 1 n< a m 2 n a m 1 n > Ein m 2 n
Summieren: bei p\u003e q und 0< a < 1 верно a p < a q , а при a > 0 - A p\u003e a q.
Die wichtigsten Eigenschaften von Grad mit irrationalen Indikatoren
Alle oben beschriebenen Eigenschaften können auf einen solchen Grad erweitert werden, der einen Grad mit rationalen Indikatoren hat. Dies folgt aus seiner Definition, die wir in einem der vorherigen Artikel gegeben haben. Wir formulieren diese Eigenschaften (Bedingungen: A\u003e 0, B\u003e 0, Indikatoren P und Q - irrationale Zahlen):
Definition 4.
1. a p · a q \u003d a p + q
2. A p: a q \u003d a p - q
3. (a · b) p \u003d a p · b p
4. (a: b) p \u003d a p: b p
5. (a p) q \u003d a p · q
6. A P.< b p верно при любых положительных a и b , если a < b и p – иррациональное число больше 0 ; если p меньше 0 , то a p > B S.
7. A P.< a q верно, если p и q – иррациональные числа, p < q , 0 < a < 1 ; если a > 0, dann ein p\u003e a q.
Somit haben alle Grad, deren Indikatoren P und Q gültige Zahlen sind, die ein\u003e 0 bereitgestellt haben, die gleichen Eigenschaften.
Wenn Sie einen Fehler im Text bemerken, wählen Sie es aus und drücken Sie STRG + ENTER
Lektion zum Thema: "Grad und seine Eigenschaften."
Der Zweck der Lektion:
Um das Wissen der Schüler zusammenzufassen: "Der Grad mit einer natürlichen Figur."
Von Studenten ein bewusstes Verständnis der Bestimmung des Grades, der Eigenschaften, der Fähigkeit, sie anzuwenden, zu erreichen.
Anwenden von Wissen, Können für verschiedene Aufgaben unterrichten.
Erstellen Sie eine Bedingung für die Manifestation der Unabhängigkeit, Ausdauer, geistiger Aktivität, der Liebe zur Mathematik instillieren.
Ausrüstung: Perfektionen, Karten, Tests, Tische.
Die Lektion ist so konzipiert, dass sie Wissen, Student, Student auf den Eigenschaften des Grads mit einem natürlichen Indikator systematisieren und zusammenfassen. Das Material der Lektion bildet mathematisches Wissen bei Kindern und entwickelt Interesse an diesem Thema, dem Horizont im historischen Aspekt.
Fortschritt.
Nachrichtenthemen und Ziele.
Heute haben wir eine allgemeine Lektion zum Thema "Abschluss mit dem natürlichen Indikator und seinen Eigenschaften".
Die Aufgabe unserer Lektion wiederholt das gesamte Material, das übergeht und sich auf die Kontrollarbeit vorbereitet.
Überprüfen Sie Ihre Hausaufgaben.
(Zweck: Überprüfen Sie die Assimilation der Übung in den Grad, die Arbeit und den Grad).
№ 238 (b) №220 (a; d) №216.
Hinter dem Brett 2 Personen mit einzelnen Karten.
a 4 ∙ A 15 A 12 ∙ A 4 a 12: A 4 A 18: A 9 (A 2) 5 (a 4) 8 (und 2. B 3) 6 (A 6 BB 4) 3 ein 0 A 0Mündliche Arbeit.
(Zweck: Wiederholen Sie die Schlüsselpunkte, die den Multiplikat- und Abteilungsalgorithmus-Grad fixieren, den Grad ausüben).
Formulieren Sie die Definition des Grads der Anzahl mit dem natürlichen Indikator.
Aktionen durchführen.
Mit welchem \u200b\u200bWert x Gleichheit wird ausgeführt.
Bestimmen Sie das Anzeichen von Expression ohne Berechnungen.
Vereinfachen.
 ; b) (A 4) 6:
(A 3) 3
; b) (A 4) 6:
(A 3) 3 Brainstorming.
( Zweck : Überprüfen Sie das unterstützende Wissen über Studierende, Gradeigenschaften).
Arbeiten mit Karten, Geschwindigkeit.
 a 6: A 4; A 10: A 3
(A 2) 2;
(a 3) 3; (A 4) 5; (A 0) 2.
a 6: A 4; A 10: A 3
(A 2) 2;
(a 3) 3; (A 4) 5; (A 0) 2. - (2a 2) 2;
(-2a 3) 3; (3a 4) 2; (-2a 2 b) 4.
Die Aufgabe: Vereinfachen Sie den Ausdruck (wir arbeiten in Paaren, die Klasse löst die Aufgabe A, B, B, Check zusammen).
(Zweck: Prüfung der Eigenschaften des Grades mit einem natürlichen Indikator.)
aber)  ; b)
; b)  ; im)
; im) 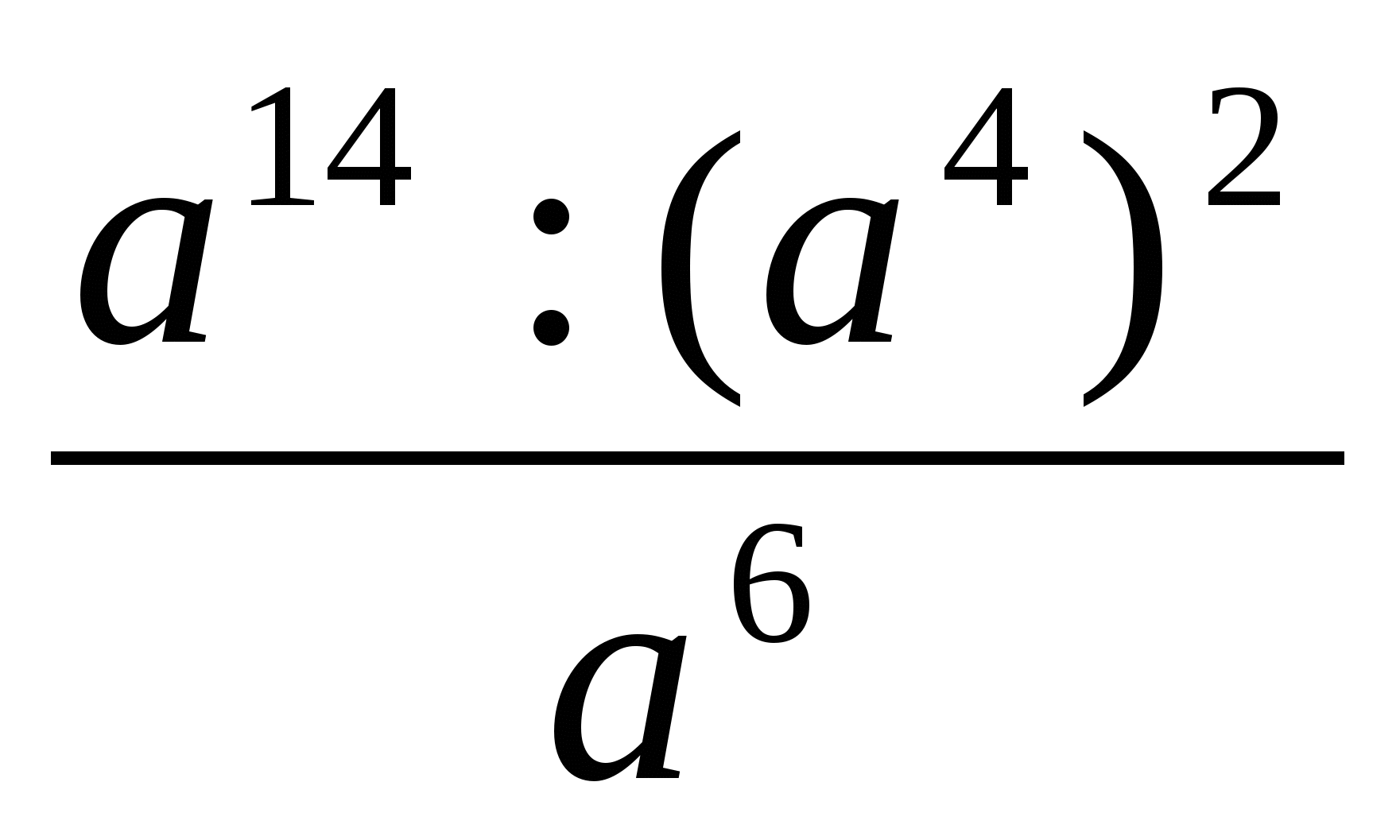
6. Berechnung:
aber) 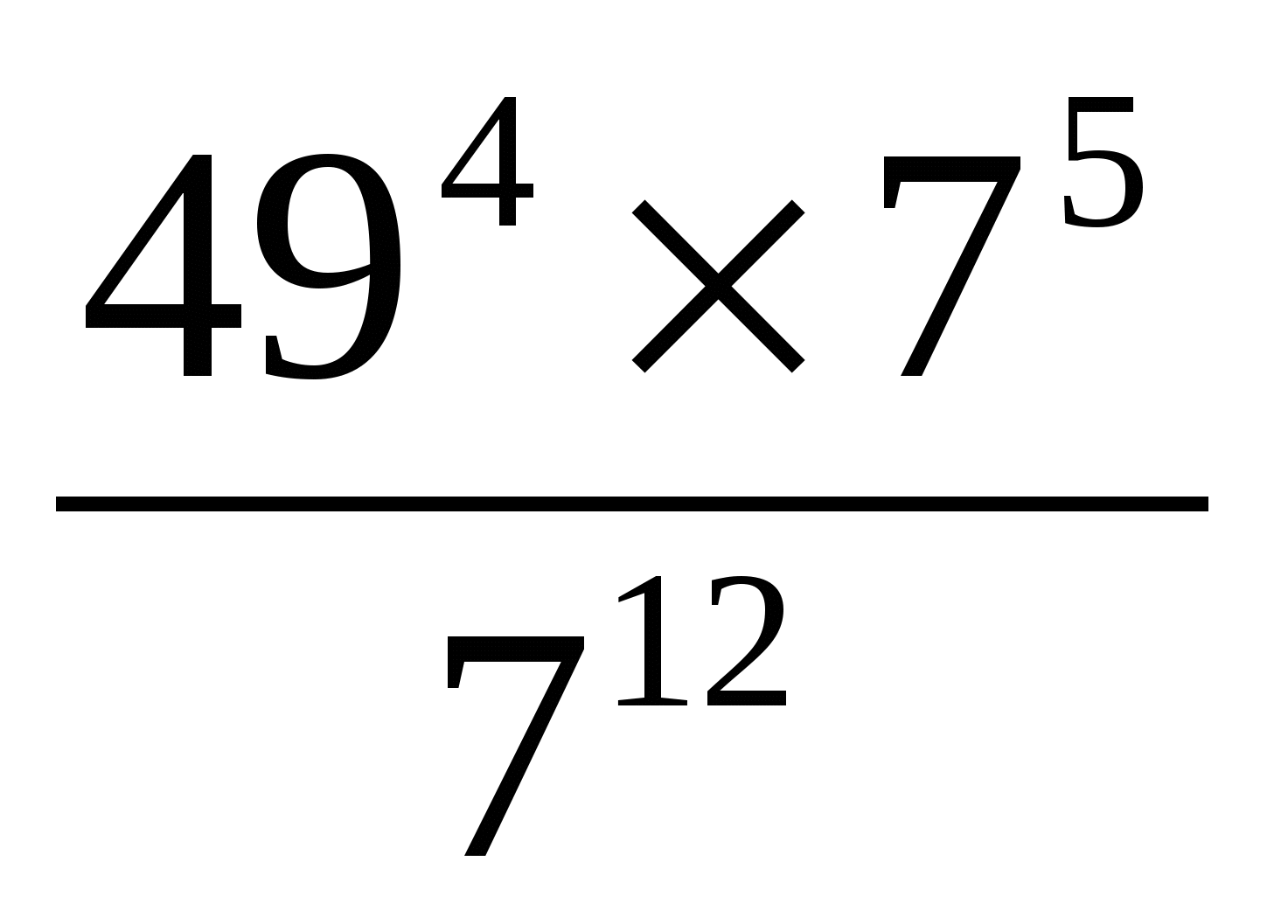 (gemeinsam )
(gemeinsam )
b)  (allein )
(allein )
im)  (allein )
(allein )
d)  (gemeinsam )
(gemeinsam )
e)  (allein ).
(allein ).
7 . Überprüfen Sie sich!
(Zweck: Entwicklung von Elementen der kreativen Aktivitäten von Studenten und Fähigkeiten, um ihre Handlungen zu steuern).
Arbeiten mit Tests, 2 Studenten für den Vorstand, Selbsttest.
І c.


Ausdrücke berechnen.

║ - im.
Vereinfachung der Ausdrücke.

Berechnung.

Ausdrücke berechnen.

D / S Home C / P (auf Karten).
Summieren der Lektion, Erhöhung der Schätzungen.
(Zweck: Damit die Schüler das Ergebnis ihrer Arbeit visuell sehen, entwickelte kognitive Interesse).
Wer begann zuerst den Studium zu studieren?
Wie baue ich ein n ?
In den ENNA-Grad für unsaber erziehen
Es ist notwendig, n zu multiplizieren Zeit
Wenn ein n Einheit - nie
Wenn mehr - dann multiplizierenund auf einem,
ich wiederhole n mal
3) Können wir die Nummer in erhöhen? n Grad, sehr schnell?
Wenn Sie den Mikrocalculator nehmen, nehmen Sie sich
Nummer A. sie erst einmal Punkte
Und dann das Zeichen der "Multiplikation" - auch -
Zeichen "Will" klicken Sie auf so viele Male
wie viele n ohne man zeigt uns
Und die Antwort ist bereit, ohne einen SchulgriffSogar.
4) Listen Sie die Eigenschaften des Grads mit einem natürlichen Indikator auf.
Schätzungen für die Lektion Wir werden nach der Überprüfung der Arbeit mit Karten mit Tests, gegebenen Tests, den Antworten der Studenten, die während der Lektion verantwortlich waren, überprüft werden.
Heute hast du heute gut gearbeitet, danke.
Literatur:
1.A.g.mordkovich algebra-7-Klasse.
2.Didaktische Materialien -7-Klasse.
3.A.G. Mordkovich-Tests - Klasse 7.
Technologisches Kartenlernen.
Klasse 7 Lektion Nr. 38
Thema: ein Verhältnis mit einem natürlichen Indikator
1. Geben Sie eine Wiederholung, Verallgemeinerung und Systematisierung von Wissen über das Thema an, konsolidieren und verbessern Sie die Fähigkeiten der einfachsten Transformationen von Ausdrücken mit Grad mit einem natürlichen Indikator, schaffen Bedingungen für die Überwachung des Ernenns von Wissen und Fähigkeiten.2. Förderung der Bildung von Fähigkeiten, um die Techniken der Verallgemeinerung, Vergleiche, der Zuweisung der Hauptsache anzuwenden, um die Ausbildung von Wissenskenntnissen in eine neue Situation, die Entwicklung einer mathematischen Aussicht, Sprache, Aufmerksamkeit und Erinnerung, die Entwicklung von pädagogische und kognitive Tätigkeit;
3. Um die Erziehung von Interesse an Mathematik, Tätigkeit, Organisation zu fördern, um die Fähigkeit der gegenseitigen und Selbstkontrolle ihrer Aktivitäten zu erziehen, die Bildung einer positiven Motivation der Lehren, Kultur der Kommunikation.
Die grundlegenden Konzepte der pädagogischen Klassen
Der Grad, der Grundlage des Grads, der Indikator, der Grad, der Grad, der Arbeit des Grades, der Abteilung der Grad, der Bau eines Grades in den Grad.
Geplantes Ergebnis
Sie lernen, das Konzept eines Grades zu betreiben, den Sinn der Aufzeichnung der Anzahl in Form eines Grades zu verstehen, um einfache Transformationen von Ausdrücken mit Grad mit einem natürlichen Indikator auszuführen.
Wird die Gelegenheit bekommen, um zu erfahren, wie Sie ganze Ausdrücke umwandeln, die ein Verhältnis mit einem natürlichen Indikator enthalten
Fachkenntnisse
Persönliches Holz:
die Fähigkeit, das Selbstwertgefühl auf der Grundlage des Kriteriums erfolgreicher Lernaktivitäten aufzunehmen.
Kognitives Holz:
die Fähigkeit, in Ihrem Wissenssystem und in Ihrem Wissen zu navigieren: einen neuen von der bereits bekannten mit Hilfe eines Lehrers zu unterscheiden; Finden Sie Antworten auf Fragen mit den in der Lektion aufgenommenen Informationen.
Verallgemeinerung und Systematisierung von Bildungsmaterial, arbeitet mit einem symbolischen Aufzeichnungen des Grads, Austauschs, Wiedergabeinformationen, die zur Lösung einer Lernaufgabe erforderlich sind
Unterabschnitt Holz:
Wenden Sie die Grad-Eigenschaften an die Umwandlung von Ausdrücken mit Grad mit einem natürlichen Indikator an
Regulierungsholz:
Die Fähigkeit, das Ziel in der Lektion mit dem Lehrer zu bestimmen und zu formulieren; Bewerten Sie Ihre Arbeit in der Lektion.Implementieren Sie ein Multiplocontrol und eine Selbststeuerung, wenn Sie Aufgaben ausführen
Kommunizieren WOOD:
In der Lage sein, Ihre Gedanken in Oral und Schreiben aufzuarbeiten, die Rede anderer zu hören und zu verstehen
Metaprivatelines.
Physik, Astronomie, Medizin, tägliches Leben
Art der Lektion
Wiederholungen, Verallgemeinerungen und Anwenden von Wissen und Fähigkeiten.
Arbeitsformen und Arbeitsmethoden
Frontal, Dampfbad, Individuum. Erklärt - illustrativ, verbale, problematische Situation, Werkstatt, gegenseitige Prüfung, Kontrolle
Ressourcenversorgung.
Komponenten UMK Makarycheva Tutorial, Projektor, Bildschirm, Computer, Präsentation, Aufgaben für Studierende, Selbstbewertungs-Blätter
Technologien, die in der Studienstunde verwendet werden
Technologie des semantischen Lesens, des problematischen Lerns, des individuellen und differenzierten Ansatzes, IKT
Kampfstudenten, AufmerksamkeitsmobilisierungGuten nachmittag Leute. Guten Tag, liebe Kollegen! Ich freue mich über alle, die sich in der heutigen offenen Lektion versammelt haben. Jungs, ich möchte mir wünschen, dass Sie fruchtbar in der Lektion arbeiten, denken Sie sorgfältig über die Antworten auf die Fragen, um sich zu beeilen, nicht zu beeilen, Klassenkameraden und ihre Antworten nicht zu unterbrechen, zu respektieren. Und ich wünsche Ihnen auch alles, was alle nur gute Noten bekommen. Viel Erfolg!
Schalten Sie sich in der Geschäftsdrhythmusstunde ein
Überprüfen Sie das Vorhandensein von allem, was für die Arbeit in der Lektion, Genauigkeit der Position der Artikel erforderlich ist. Die Fähigkeit, sich selbst zu organisieren, ist für die Arbeit konfiguriert.
2. Aktualisierung von Referenzwissen und Eintritt in das Thema
3. Mundarbeit
Jungs, jedes von Ihnen ist auf dem Schreibtisch sind geschätzte Blätter.An ihnen werden Sie Ihre Arbeit in der Lektion bewerten. Heute haben Sie heute die Gelegenheit, nicht alleine zu bekommen, sondern zwei Schätzungen: Für die Arbeit in der Lektion und für unabhängige Arbeiten.
Ihre treue, volle Antworten werden auch von "+" bewertet, aber ich werde diese Bewertung in eine andere Spalte einsetzen.
Auf dem Bildschirm sehen Sie die Rebusse, in denen die Schlüsselwörter der heutigen Lektion verschlüsselt werden. Rutschen Sie sie. (Slide 1)
leistung
 wiederholung
wiederholung
 verallgemeinerung
verallgemeinerung
Jungs, Sie erraten die Rebons richtig. Diese Worte: Grad, Wiederholung und Verallgemeinerung. Nun, mit den begabten Wörtern - Anweisungen, geben Sie das Thema der heutigen Lektion an.
Recht. Öffnen Sie das Notebook und notieren Sie die Anzahl und das Thema der Unterrichtswiederholung und eine Verallgemeinerung auf dem Thema "Grad-Eigenschaften mit einem natürlichen Indikator" (Slide 2)
Thema der Lektion, die wir entschlossen haben, und was denken Sie, was wir in der Lektion tun werden, welche Ziele vor Ihnen legen? (Slide 3)
Wiederholen und fassen Sie unser Wissen zu diesem Thema wiederholen und fassen Sie die vorhandenen Lücken, bereiten Sie sich auf das Studium des folgenden Themas "Single" vor.
Jungs, die Eigenschaften des Grads mit einem natürlichen Indikator werden oft beim Ausdruck von Werten mit Expressions-Transformationen verwendet. Die Geschwindigkeit der Berechnungen und Transformationen, die mit den Eigenschaften des Grades mit dem natürlichen Indikator verbunden sind, wird durch die Einführung der Verwendung diktiert.
So werden wir heute Ihr Wissen und Ihre Fähigkeiten auf diesem Thema wiederholen und zusammenfassen. Mündlich müssen Sie eine Reihe von Aufgaben lösen und an die verbale Gruppierung von Eigenschaften erinnern und den Grad mit einem natürlichen Indikator bestimmen.
Epigraph Zu der Lektion, dem Wort des großen russischen Wissenschaftlers M.v. Volonosov ", lassen Sie jemanden versuchen, die Mathematik des Grades auszuschlagen, und er wird sehen, dass sie nicht weit ohne sie gehen werden"
(Slide 4)
Was denkst du ist das Recht auf Wissenschaftler?
Warum brauchen wir Abschlüsse?
Wo haben sie den weit verbreiteten Gebrauch gefunden? (in Physik, Astronomie, Medizin)
Richtig, und jetzt wiederholen wir wieder, was ist der Grad?
Was heißt A undn. In der Umfang aufnehmen?
Welche Maßnahmen können mit Grad durchgeführt werden? (Folien 5 -11)
Und jetzt fassen wir zusammen. Sie haben ein Stück Flugblätter mit Aufgaben .
1. SLEVA zeigte den Beginn der Definitionen des Rechts an, die Definitionen zu beenden. Verbinden Sie die richtigen Anweisungen (Slide 12)
Verbinden Sie die relevanten Teile der Definition.a) Beim Multiplizieren von Grad mit den gleichen Basen ...
1) Die Grundlage des Grades
b) Bei der Trennung von Graden mit den gleichen Basen ....
2) Exponent
c) Nummer A-Anruf
3) Das Produkt von n Multiplizierern, von denen jeder gleich a ist.
d) beim Errichten eines Grads in einem ...
4) ... Die Basis bleibt gleich und die Indikatoren sind gefaltet.
e) der Grad der Nummer A mit einem natürlichen Indikator N, groß 1, genannt
5) ... Die Basis bleibt gleich und die Indikatoren sind variabel.
e)Nummern.anruf
6) Grad.
g)Ausdruck A. n. Anruf
7) ... Die Basis bleibt gleich, und die Indikatoren werden abgezogen.
2. Ändern Sie nun die Blätter mit einem Nachbarn im Schreibtisch, bewerten Sie es und stellen Sie es mit. Diese Bewertung wird dieses Bewertungsblatt einsetzen.
Und jetzt überprüfen wir, ob Sie die Aufgabe richtig abgeschlossen haben.
Gay Rebruses, Wörter definieren - Tipps.
Versuche, das Thema der Lektion zu setzen.
Notieren Sie sich in dem Notebook die Nummer und den Themenstunden.
Fragen beantworten
Partnerarbeit. Lesen Sie die Aufgabe, denken Sie daran.
Verbinden Sie Teile von Definitionen
Exchange-Notebooks.
Führen Sie einen gegenseitigen Test der Ergebnisse aus, setzen Sie die Bewertungen in die Partei an den Nachbarn.
4.pizkultminutka.
Hände angehoben und schockiert -
dies sind Bäume im Wald,
Hände gebogen, Bürsten schütteln -
Der Wind raste das Laub.
An den Seiten der Hand, reibungslos realisierbar -
Vögel südlich so fliegen
Wenn sie sich hinsetzen, werden wir leise zeigen -
Hände gefaltet wie diese!
Aktionen parallel zum Lehrer durchführen
5. Übertragen von erworbenen Kenntnissen, ihrer primären Verwendung bei neuen oder veränderten Bedingungen, um Fähigkeiten zu bilden.
1. Ich biete Ihnen den folgenden Job an: Sie haben auf den Karten der Karte. Sie müssen Aufgaben durchführen, d. H. Notieren Sie eine Antwort in Form eines Abschlusses mit der Basis von C, und Sie erfahren den Namen und den Namen der großen französischen Mathematik, die die allgemein anerkannte Bezeichnung von Grad eingeführt hat. (Slide 14)
5VON 8 : VON 6
(VON 4 ) 3 VON
(VON 4 ) 3
VON 4 VON 5 VON 0
VON 5 VON 3 : VON 6
VON 16 : VON 8
VON 14 VON 8
10.
(VON 3 ) 5
Antwort: Rene Descartes.
Geschichte über Biografien Rene decartet (Folien 15 - 17)
Jungs, und jetzt machen wir die folgende Aufgabe.
2. O. bieten Sie an, welche Antworten richtig sind und was falsch ist. (Slide 18 - 19)
setzen Sie die wahre Antwort in Übereinstimmung mit 1, FALSE - 0.
nach Erhalt eines bestellten Satzes und Nullen erfahren Sie die richtige Antwort und definieren den Namen und den Nachnamen der ersten russischen Frau - Mathematik.
aber) X. 2 x. 3 \u003d X. 5
b.) S. 3 s. 5 s. 8 = s. 16
im) X. 7 : x. 4 \u003d X. 28
d) (c.+ d.) 8 : ( c.+ d.) 7 = c.+ d.
e) (x. 5 ) 6 = x. 30
Wählen Sie ihren Namen aus den vier Namen berühmter Frauen, von denen jede einem Satz von Einheiten und Nullen entspricht:
ADU gegen Lavleys - 11001
Sophie Germain - 10101
Ekaterina Dashkov - 11101
Sophia Kovalevskaya - 11011
Aus der Biographie von Sofia Kovalevskaya (Slide 20)
Führen Sie eine Aufgabe aus, der Nachname und der Name der französischen Mathematik werden bestimmt
Hören Sie, berücksichtigen Sie Folien
Beachten Sie die treue und falsche Antworten, schreiben Sie den resultierenden Code, nach dem der Name der ersten russischen Frau bestimmt ist - Mathematik.
6. Kontrolle und Beurteilung des Wissens Unabhängige Erfüllung von Aufgaben unter der Kontrolle des Lehrers.
Und jetzt musst du den Check machen. Sie haben eine Karte mit Aufgaben unterschiedlicher Farbe. Die Farbe entspricht der Komplexität der Task (auf "3", auf "4", auf "5"), wählen Sie sich selbst, die Aufgabe, auf deren Bewertung Sie aufführen und zur Arbeit fortfahren. (Folie 21)
Auf 3"
1. Stellen Sie sich ein Produkt vor:
aber) ; b) ;
im) ; d) .
2. Führen Sie Folgendes aus:
( m. 3 ) 7 ; ( k. 4 ) 5 ; (2 2 ) 3; (3 2 ) 5 ; ( m. 3 ) 2 ; ( eIN. x. ) y.
Auf "4"
1. Umsetzung in Form eines Grades.
a) H. 5 H. 8 ; Boo. 2 W. 9 ; um 2 6 · 2 4 ; d)m. 2 m. 5 m. 4 ;
e)x. 6 ∙ X. 3 ∙ X. 7 ; e) (-7) 3 ∙ (–7) 2 ∙ (–7) 9 .
2 Stellen Sie sich Privat in Form eines Grads vor:
aber)x. 8 : X. 4 ; b) (-0,5) 10 : (–0,5) 8 ;
c) x. 5 : H. 3 ; d) u. 10 : U. 10 ; D 2. 6 : 2 4 ; e);
auf "5"
1. Füllen Sie die Aktion:
a) A. 4 · aber · aber 3 a b) (7 h. ) 2 c) R. · r. 2 · r. 0
d) S. · von 3 · c d) t · t. 4 · ( t. 2 ) 2 · t. 0
e) (2 3 ) 7 : (2 5 ) 3 g) -h. 3 · (– h. ) 4
h) (r. 2 ) 4 : r. 5 und) (3 4 ) 2 · (3. 2 ) 3 : 3 11
2. Vereinfinden:
aber) x. 3 · ( x. 2) 5 b) ( eIN. 2) 3 · ( eIN. 4 ) 2
b) ( eIN. 3) 2 · eIN. 5 g) ( x. 2) 5 · ( x. 5 )
Selbstständige Arbeit
Aufgaben in Notebooks durchführen
7. Die Ergebnisse der Lektion
Verallgemeinerung der in der Lektion erhaltenen Informationen.Überprüfung der Arbeit, Bewertung. Identifizieren Sie die Schwierigkeiten in der Lektion
8. Reflexion.
Was ist mit dem Konzept des Grades in passiert?XVII. Ein Jahrhundert können wir sich vorhersagen. Versuchen Sie dies dazu, die Frage zu beantworten: Ist es möglich, einen negativen Grad oder ein negatives Grad oder ein fraktioniert zu bauen? Dies ist jedoch das Thema unserer zukünftigen Studie.
Schätzungen für die Lektion
Jungs, unsere Lektion, die ich das nächste Gleichnis beenden möchte.
Gleichnis. Es war ein Sage und um drei Leute zu treffen, die einen Wagen mit Steinen unter der heißen Sonne trugen. Der Sage blieb stehen und fragte jeden in der Frage. Der erste fragte: "Was hast du einen ganzen Tag gemacht?" Und er antwortete mit einem Grinsen, dass die verdammten Steine \u200b\u200bden ganzen Tag fuhren. Der zweite Sage fragte: "Und was hast du den ganzen Tag gemacht", und er antwortete: "Und ich erfüllte mich gewissenhaft meinen Job." Und der dritte lächelte, sein Gesicht beleuchtete Freude und Freude: "Und ich nahm an dem Bau des Tempels teil!"
Jungs, Antwort, was hast du heute in der Lektion gemacht? Machen Sie es einfach im Blech des Selbstwertgefühls. Fahren Sie den Kreis in jeder Spalte, die Anweisung, die sich auf Sie bezieht.
In einem Blatt des Selbstwertgefühls müssen Sie die Phrasen betonen, die die Arbeit des Studenten in der Lektion in drei Richtungen kennzeichnen.
Unsere Lektion ist abgeschlossen. Danke an jeden für die Arbeit in der Lektion!
Fragen beantworten
Bewerten ihre Arbeit in der Lektion.
Hinweis in der Satzkarte und kennzeichnen ihre Arbeit in der Lektion.
algebra 7. Klasse
mathematischer Lehrer
zweig mbootssosh
in S.poletaevo zuva i.p.
Flug 2016.
Gegenstand: « Eigenschaften des Grades mit einem natürlichen Indikator»
ZIEL
- Wiederholung, Verallgemeinerung und Systematisierung des untersuchten Materials zum Thema "Eigenschaften des Grades mit einem natürlichen Indikator".
- Überprüfen Sie das Wissen der Schüler auf diesem Thema.
- Anwendung des Wissens, das bei der Durchführung verschiedener Aufgaben gewonnen wurde.
AUFGABEN
gegenstand :
wiederholen, fassen und systematisieren Sie das Wissen über das Thema zusammen; Erstellen Sie Überwachungsbedingungen (Interconnection) Lernkenntnisse und Fähigkeiten;setzen Sie die Bildung der Motivation der Schüler fort, das Thema zu studieren;
mEDAGERT:
entwickeln Sie einen operativen Denkstil; Fördern Sie den Erwerb der teilnehmenden Kommunikationsfähigkeiten, wenn sie zusammenarbeiten; intensivieren ihr kreatives Denken; P.zur Geburt der Bildung bestimmter Kompetenzen von Studenten, die zu ihrer wirksamen Sozialisierung beitragen werden; Fähigkeiten der Selbstbildung und Selbstbildung.
persönlich:
kultur erziehen, zur Bildung von persönlichen Qualitäten beitragen, die auf eine freundliche, tolerante Einstellung, Menschen, Lebensdauer, ausgerichtet sind; erziehen Sie die Initiative und Unabhängigkeit in Aktivitäten; Bess, um das Bedürfnis nach einem studierenden Thema zu verstehen, um eine erfolgreiche Vorbereitung auf die staatliche endgültige Zertifizierung zu erzielen.
Art der Lektion
verallgemeinerungsstunde und Systematisierung Zun.
Ausrüstung: Computer, Projektor,bildschirm zum Projektion, Board, Verteilungsmaterial.
Software: Windows 7: MS Office 2007 (Erforderliche Anwendung -Steckdose).
Vorbereitungsstufe:
präsentation der "Eigenschaften des Grades mit einem natürlichen Indikator";
handzettel;
schaltungsblatt.
Struktur
Zeit organisieren. Die Einstellung von Zielen und Zielen der Lektion beträgt 3 Minuten.
Aktualisierung, Systematisierung von Referenzwissen - 8 Minuten.
Praktischer Teil -28 Minuten.
Verallgemeinerung, Rücknahme -3-minute.
Hausaufgaben - 1 Minute.
Reflexion - 2 Minuten.
Ideenstunde
Überprüfen Sie in einer interessanten und effektiven Form von Zonenstudenten zu diesem Thema.
Organisation der Lektion. Die Lektion wird in der Klasse 7 durchgeführt. Die Jungs arbeiten paarweise, unabhängig, der Lehrer fungiert als Beobachterberater.
Während der Klassen
Zeit organisieren:
Hallo Leute! Heute haben wir ein ungewöhnliches Lektionsspiel. Jeder von Ihnen ist mit einer großartigen Gelegenheit ausgestattet, um sich selbst auszudrücken, zeigen Sie Ihr Wissen. Vielleicht enthüllen Sie während der Lektion die verborgenen Fähigkeiten, die in der Zukunft für Sie nützlich sein werden.
Jeder hat ein Testblatt und Karten auf dem Tisch, um Aufgaben in ihnen auszuführen. Nehmen Sie in die Hände eines Testblatts, es braucht Sie, damit Sie Ihr Wissen während der Lektion zu schätzen wissen. Unterschreib es.
Also lade ich Sie zu einer Lektion ein!
Jungs, schauen Sie sich den Bildschirm an und hören Sie sich das Gedicht an.
Slide №1.
Multiplizieren und teilen
Grad in dem Grad ...
Eigenschaften, die uns uns vertraut sind
Und vor langer Zeit sind nicht neu.
Fünf einfache Regeln dieser
Jeder in der Klasse antwortete
Aber wenn die Eigenschaften vergessen haben,
Überlegen Sie, Sie haben das Beispiel nicht entschieden!
Und ohne Probleme in der Schule leben
Lady Ich treffe Ihnen:
Willst du nicht vergessen?
Versuchen Sie, nur auswendig zu lernen!
Beantworte die Frage:
1) Welche Maßnahmen werden darin erwähnt?
2) Was denkst du, über das wir heute in der Lektion sprechen werden?
Das Thema unserer Lektion:
"Gradeigenschaften mit einem natürlichen Indikator" (Slide3).
Setzen Sie die Ziele und Ziele der Lektion
In der Lektion wiederholen wir das Material auf dem Thema "Eigenschaften des Grades mit einem natürlichen Indikator".
Mal sehen, wie Sie gelernt haben, sich mit den gleichen Gründen zu multiplizieren und zu teilen, sowie den Grad in den Grad anheben
Aktualisierung von Referenzwissen. Systematisierung des theoretischen Materials.
1) Mundarbeit
Wir werden oral arbeiten
1) Word Die Eigenschaften mit einem natürlichen Indikator.
2) Füllen Sie die Leerzeichen aus: (Slide 4)
1)5 12 : 5 5 =5 7 2) 5 7 ∙ 5 17 = 5 24 3) 5 24 : 125= 5 21 4)(5 0 ) 2 ∙5 24 =5 24
5)5 12 ∙ 5 12 = (5 8 ) 3 6)(3 12 ) 2 = 3 24 7) 13 0 ∙ 13 64 = 13 64
3) Was ist der Wert des Ausdrucks:(Slide5-9)
ein m ∙ a n; (Ein m + n) a m: a n (a m-n); (a m) n; Ein 1; Ein 0.
2) Überprüfung des theoretischen Teils (KARTE SPINITION1)
Und nimm jetzt eine Kartennummer 1 in meinen Händen undfülle die Lücken
1) Wenn ein gerumder Zahlenanzeige, ist der Wert des Grads immer _______________
2) Wenn der Indikator eine ungerade Zahl ist, fällt der Wert des Grads mit dem Zeichen ____ zusammen.
3) Die Arbeit der Gradea n · a k \u003d a n + k
Beim Multiplizieren von Grad mit den gleichen Basen ist es notwendig, ____________ und die Indikatoren von Grad ________ zu begrenzen.
4) Privatgradea n: a k \u003d a n - k
Bei der Trennung von Grad mit den gleichen Basen ist es notwendig, _____ und aus der Abteilung von ____________________________ zu stützen.
5) der Bau eines Grades in den Grad (a n) k \u003d a nk
Wenn der Grad in einem Grad errichtet wird, ist das Fundament _______ notwendig _______ und die Indikatoren von Grad ______.
Überprüfen Sie die Antworten. (Folien 10-13)
Hauptteil
3) Und jetzt öffnen Sie Notebooks, schreiben Sie die Nummer 28.01 14g, coole Arbeit
Spiel "Clapper. » (Folie 14)
Erstellen Sie die Aufgaben in Notizbüchern selbst
Folgen Sie den Schritten: a)h.11 ∙ x ∙ x2 b)h.14 : H.5 c) (und4 ) 3 d) (-)2 .
Vergleichen Sie den Wert der Ausdrücke mit Null: a) (- 5)7 , b) (- 6)18 ,
um 4)11 . ( -4) 8 d) (- 5) 18 ∙ (- 5) 6 , e) - (- 4)8 .
Berechnen Sie den Wert des Ausdrucks:
a) -1 ∙ 3 2, b) (- 1 ∙ 3) 2 c) 1 ∙ (-3) 2, g) - (2 ∙ 3) 2, d) 1 2 ∙ (-3) 2
Wir prüfen, ob die Antwort nicht das Recht ist, eine Baumwolle in den Händen herzustellen.
Berechnen Sie die Anzahl der Punkte und bringen Sie sie auf das Kreditblatt.
4) Und jetzt werden wir Gymnastik für die Augen ausführen, wir werden die Spannung entfernen, und wir werden weiter arbeiten. Folgen Sie sorgfältig der Bewegung von Objekten
Start! (Schlitten 15,16,17,18).
5) Und jetzt werde ich mit der folgenden Art unserer Arbeit fortfahren. (Card2)
Notieren Sie die Antwort in Form eines Grads mit der Basis VON und Sie erfahren den Namen und den Namen der großen französischen Mathematik, die zunächst das Konzept des Nummerns eingeführt hat.
Erraten Sie den Nachnamen der Wissenschaftler Mathematik.
| 1. | VON 5 ∙ S. 3 | 6. | VON 7 : VON 5 |
| 2. | VON 8 : VON 6 | 7. | (VON 4 ) 3 ∙ S. |
| 3, | (VON 4 ) 3 | 8. | VON 4 ∙ VON 5 ∙ S. 0 |
| 4. | VON 5 ∙ S. 3 : VON 6 | 9. | VON 16 : VON 8 |
| 5. | VON 14 ∙ S. 8 | 10. | (VON 3 ) 5 |
ÜBER tVETY: Rene Descartes
| R. | Sch | M. | Yu. | ZU | N. | ABER | T. | E. | D. |
|||||
| VON 8 | VON 5 | VON 1 | VON 40 | VON 13 | VON 12 | VON 9 | VON 15 | VON 2 | VON 22 |
Und jetzt höre ich auf die Botschaft des Schülers über Rene Descartes
Rene Descartes wurde am 21. März 1596 in der kleinen Stadt La Ge in der Turnya geboren. Die Gattung Descartes gehörte zu einem nicht unschuldigen offiziellen Adel. Kindheit Rena im Inhaber verbracht. Im Jahr 1612 wurde decartes die Fertigschule. Er verbrachte achteinhalb Jahre alt. Descartes fand seinen Platz nicht sofort im Leben. Der Adelige von Ursprung, der von einem College in La Flea absolviert, taucht er in das säkulare Leben von Paris und wirft dann alles in der Wissenschaft. Descartes nahm in seinem System einen besonderen Platz in seinem System zur Mathematik, er gilg ihre Prinzipien für die Festlegung der Wahrheit mit einem Modell für andere Wissenschaften. Der beträchtliche Verdienst von Descartes war die Einführung von günstigen Bezeichnungen, die bis heute erhalten wurden: lateinische Buchstaben x, y, z für unbekannte; A, B, C - für Koeffizienten für Grad. Die Interessen von Descartes sind nicht auf Mathematik beschränkt, sondern zählen Mechanik, Optik, Biologie. Im Jahre 1649 zog sich Descartes nach langem Zögern nach Schweden. Diese Entscheidung war für seine Gesundheit tödlich. Nach einem halben Jahr starben Descartes an der Pneumonie.
6) Arbeit an der Tafel:
1. Entscheidet die Gleichung
A) x 4 ∙ (x 5) 2 / x 20: x 8 \u003d 49
B) (T 7 ∙ T 17): (T 0 ∙ T 21) \u003d -125
2. Berechnen Sie den Wert des Ausdrucks:
(5-×) 2 -2x 3 + 3x 2 -4x + x - x 0
a) bei x \u003d -1
b) bei x \u003d 2 unabhängig voneinander
7) Nehmen Sie eine Kartennummer 3. Führen Sie einen Test aus
| Möglichkeit 1 | Option 2. |
| 1. Grad 2 fit17 : 2 5 2 12 2 45 2. Schreiben Sie in Form von Grad (x + y) (x + y) \u003d x 2 + in 2 (x + y) 2 2 (x + y) 3. Ersetzen * Grad zur Gleichheit undfünf · * \u003d A 15. a 10 und 3. (A 7) 5? a) und 12 b) und 5 c) und 35 3 = 8 15 8 12 6.Finden Sie den Wert des Fraci | 1. Abschlüsse 99 : 9 7 9 16 9 63 2. Schreiben Sie in Form von Grad (X-Y) (X-Y) \u003d ... x 2 - 2 (X-y) 2 2 (x-y) 3. Ersetzen * Grad zur Gleichstellungb 9 · * \u003d B 18. b 17. b 1 1. 4. Was ist der Wert des Ausdrucks(von 6) 4? a) mit 10 b) mit 6 c) ab 24 5. Wählen Sie aus den vorgeschlagenen Optionen die, die * in Gleichstellung ersetzt werden kann (*)3 = 5 24 5 21 6.Finden Sie den Wert des Fraci |
Überprüfen Sie die Arbeiten des anderen und legen Sie eine Bewertung an Ihre Kameraden in das Testblatt.
| 1 Option | aber | b. | b. | von | b. | 3 |
| Option 2 | aber | b. | von | von | aber | 4 |
Zusätzliche Aufgaben für starke Studenten
Jede Aufgabe wird separat geschätzt.
Finden Sie den Wert des Ausdrucks:
8) Und jetzt werden wir die Wirksamkeit unserer Lektion ansehen ( Slide 19)
Um dies zu tun, löschen Sie die Aufgabe, die Buchstaben, die den Antworten entsprechen.
Aahustlkrichgnamm.
Den Ausdruck vereinfachen:
| 1. | C 4 ∙ C 3 | 5. | (VON 2 ) 3 ∙ VON 5 |
| 2. | (Von 5) 3 | 6. | VON 6 ∙ VON 5 : VON 10 |
| 3. | Von 11: ab 6 | 7. | (VON 4 ) 3 ∙ S. 2 |
| 4. | Von 5 ∙ von 5: mit |
Chiffre: ABER - Mit 7. IM- Mit 15. G - VON Und - Mit 30. Zu - Mit 9. M - Von 14. N - Mit 13. ÜBER - Ab 12. R - Von 11. VON - Mit 5. T - Von 8. H - Mit 3.
Welches Wort hast du getan? Antwort: Ausgezeichnet! (Folie 20)
Summieren, Bewertung, Markierung (Folie 21)
Seien wir unsere Lektion zusammenfassen sowie erfolgreich wiederholten, zusammengefasst und systematisierten das Wissen über das Thema "Eigenschaften des Grads mit einem natürlichen Indikator".
Nehmen Sie die Kreditwürdige und zählen Sie die Gesamtzahl der Punkte und schreiben Sie sie in die Zeile der abschließenden Beurteilung
Stand, der 29-32 Punkte erzielt hat: Die Bewertung ist
25-28 Punkte: Bewertung - Easy
20-24 Punkte: Bewertung - zufriedenstellend
Ich werde erneut die Richtigkeit der Ausführung von Aufgaben auf den Karten überprüfen, um Ihre Ergebnisse mit den Ergebnissen im Kreditblatt zu verweisen. Schätzungen in der Zeitschrift
Und für aktive Arbeiten in der Unterrichtsunterricht:
Die Jungs bitten Sie, Ihre Aktivität in der Lektion zu bewerten. Modement im Stimmungsblatt.
| Kreditblatt |
||
| Familienname | Auswertung |
|
| 1.Torhesitsetisches Teil. | ||
| 2. Klappenkarte | ||
| 3. testen | ||
| 4. "SIFR" | ||
| Zusätzlicher Teil | ||
| Abschlussnote: | ||
| Emotionale Beurteilung | Über mich | Über eine Lektion |
| Zufrieden | ||
| Unzufrieden | ||
Hausaufgaben (Slide 22)
Machen Sie ein Kreuzworträtsel mit dem Keyword-Grad. In der nächsten Lektion werden wir uns die interessanteste Arbeit ansehen.
№ 567
Liste der verwendeten Quellen
- Lehrbuch "Algebra-Klasse 7".
- Gedicht. http://yandex.ru/yandsearch.
- NICHT. Schurkov. Kultur einer modernen Lektion. M.: Russische Pädagogische Agentur, 1997.
- EIN V. Petrov. Methodische und methodische Grundlagen der personenbezogenen Computerausbildung. Wolgograd. "Änderung", 2001.
- WIE. Belkin. Erfolgssituation. So erstellen Sie es. M.: "Erleuchtung", 1991.
- Informatik und Bildung №3. Betriebsstil denken, 2003




