Was hat das dreieck. Wie heißen die Winkel eines Dreiecks? Beziehungen in einem Dreieck

Wenn drei Punkte, die nicht auf einer Geraden liegen, durch Segmente verbunden werden, erhalten wir ein Dreieck. Eine der Seiten eines Dreiecks wird oft als Basis bezeichnet.

Satz. Die Summe der Winkel eines Dreiecks ist 180 0

Sind alle drei Winkel eines Dreiecks spitz, so heißt das Dreieck spitzwinklig.

Wenn einer der Winkel eines Dreiecks stumpf ist, wird das Dreieck aufgerufen stumpf.

Wenn einer der Winkel eines Dreiecks recht ist, dann heißt das Dreieck rechteckig. Die Seite eines rechtwinkligen Dreiecks, die dem rechten Winkel gegenüberliegt, heißt Hypotenuse, und die anderen beiden Seiten Beine.

In jedem Dreieck liegt der größeren Seite ein größerer Winkel gegenüber; gegenüberliegende gleiche Seiten - gleiche Winkel und umgekehrt. Jede Seite eines Dreiecks ist kleiner als die Summe der beiden anderen Seiten und auch größer als die Differenz der beiden anderen Seiten.

Wenn wir eine der Seiten des Dreiecks fortsetzen, erhalten wir die äußere Ecke. Winkel ABD - extern.

Zeichen der Gleichheit von Dreiecken

Wenn zwei Dreiecke kongruent sind, dann sind die Elemente (Seiten und Winkel) des einen Dreiecks jeweils gleich den Elementen des anderen Dreiecks.

Satz. Zwei Dreiecke sind kongruent, wenn zwei Seiten und der Winkel zwischen ihnen des einen Dreiecks jeweils gleich zwei Seiten und der Winkel zwischen ihnen des anderen sind.

Satz. Zwei Dreiecke sind kongruent, wenn eine Seite und zwei benachbarte Winkel eines Dreiecks gleich einer Seite und zwei benachbarten Winkeln des anderen sind.

Satz. Zwei Dreiecke sind kongruent, wenn drei Seiten des einen Dreiecks jeweils gleich drei Seiten des anderen sind.

Median, Winkelhalbierende und Höhe eines Dreiecks

Die Strecke, die die Spitze eines Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet, heißt Median Dreieck.

Ein Strahl, der vom Scheitelpunkt eines Winkels ausgeht und ihn in zwei gleiche Winkel teilt, wird genannt Winkelhalbierende. Die Winkelhalbierende teilt die gegenüberliegende Seite in Teile, die proportional zu den angrenzenden Seiten sind.

Die Senkrechte, die von der Spitze eines Dreiecks zu der Linie gezogen wird, die die gegenüberliegende Seite enthält, heißt Höhe Dreieck.

Wunderbare Dreieckspunkte. 1) Die Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt.

2) Die Mittelsenkrechten zu den Seiten des Dreiecks schneiden sich in einem Punkt.

3) Die Höhen des Dreiecks (bzw. deren Verlängerungen) schneiden sich in einem Punkt.

4) Die Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt.

Gleichschenkligen Dreiecks

Ein Dreieck heißt gleichschenklig, wenn zwei seiner Seiten gleich sind. Gleiche Seiten werden aufgerufen Seiten, und der Dritte Basis gleichschenkligen Dreiecks.

Ein Dreieck, in dem alle Seiten gleich sind, heißt gleichseitiges Dreieck.

Satz. In einem gleichschenkligen Dreieck sind die Winkel an der Basis gleich.

Satz. In einem gleichschenkligen Dreieck ist die zur Basis gezogene Winkelhalbierende der Median und die Höhe.

Die Wissenschaft der Geometrie sagt uns, was ein Dreieck, ein Quadrat oder ein Würfel ist. In der modernen Welt wird es ausnahmslos von allen in den Schulen studiert. Auch eine Wissenschaft, die direkt untersucht, was ein Dreieck ist und welche Eigenschaften es hat, ist die Trigonometrie. Sie untersucht alle mit Daten verbundenen Phänomene im Detail.Wir werden in unserem Artikel darüber sprechen, was ein Dreieck heute ist. Ihre Typen werden unten beschrieben, ebenso wie einige Theoreme, die sich auf sie beziehen.

Was ist ein Dreieck? Definition

Dies ist ein flaches Polygon. Es hat drei Ecken, was aus seinem Namen hervorgeht. Es hat auch drei Seiten und drei Eckpunkte, von denen die ersten Segmente und die zweiten Punkte sind. Wenn du weißt, welchen zwei Winkeln gleich sind, kannst du den dritten finden, indem du die Summe der ersten beiden von der Zahl 180 subtrahierst.

Was sind Dreiecke?

Sie lassen sich nach verschiedenen Kriterien klassifizieren.

Zunächst werden sie in spitzwinklige, stumpfwinklige und rechteckige unterteilt. Die ersten haben spitze Winkel, dh solche, die weniger als 90 Grad betragen. Bei stumpfen Winkeln ist einer der Winkel stumpf, das heißt einer, der größer als 90 Grad ist, die anderen beiden sind spitz. Zu den spitzen Dreiecken gehören auch gleichseitige Dreiecke. Bei solchen Dreiecken sind alle Seiten und Winkel gleich. Sie sind alle gleich 60 Grad, dies kann leicht berechnet werden, indem die Summe aller Winkel (180) durch drei geteilt wird.

Rechtwinkliges Dreieck

Es ist unmöglich, nicht darüber zu sprechen, was ein rechtwinkliges Dreieck ist.

Eine solche Figur hat einen Winkel von 90 Grad (gerade), dh zwei ihrer Seiten sind senkrecht. Die anderen beiden Winkel sind spitz. Sie können gleich sein, dann wird es gleichschenklig. Der Satz des Pythagoras bezieht sich auf das rechtwinklige Dreieck. Mit seiner Hilfe können Sie die dritte Seite finden, wenn Sie die ersten beiden kennen. Wenn Sie nach diesem Satz das Quadrat des einen Beins zum Quadrat des anderen addieren, erhalten Sie das Quadrat der Hypotenuse. Das Quadrat des Beins kann berechnet werden, indem das Quadrat des bekannten Beins vom Quadrat der Hypotenuse subtrahiert wird. Wenn wir darüber sprechen, was ein Dreieck ist, können wir uns an die Gleichschenkel erinnern. Dies ist eine, bei der zwei der Seiten gleich sind und zwei der Winkel ebenfalls gleich sind.

Was ist das Bein und die Hypotenuse?

Das Bein ist eine der Seiten eines Dreiecks, die einen Winkel von 90 Grad bilden. Die Hypotenuse ist die verbleibende Seite, die dem rechten Winkel gegenüberliegt. Von ihm aus kann eine Senkrechte auf das Bein abgesenkt werden. Das Verhältnis des angrenzenden Beins zur Hypotenuse wird als Kosinus bezeichnet, und das Gegenteil wird als Sinus bezeichnet.

- was sind seine Eigenschaften?

Es ist rechteckig. Seine Beine sind drei und vier, und die Hypotenuse ist fünf. Wenn Sie gesehen haben, dass die Beine dieses Dreiecks gleich drei und vier sind, können Sie sicher sein, dass die Hypotenuse gleich fünf ist. Außerdem kann gemäß diesem Prinzip leicht bestimmt werden, dass das Bein gleich drei ist, wenn das zweite gleich vier ist und die Hypotenuse fünf ist. Um diese Aussage zu beweisen, können Sie den Satz des Pythagoras anwenden. Wenn zwei Beine 3 und 4 sind, dann 9 + 16 \u003d 25, ist die Wurzel von 25 5, dh die Hypotenuse ist 5. Ein ägyptisches Dreieck wird auch als rechtwinkliges Dreieck bezeichnet, dessen Seiten 6, 8 und 10 sind ; 9, 12 und 15 und andere Zahlen mit einem Verhältnis von 3:4:5.

Was könnte noch ein Dreieck sein?

Dreiecke können auch eingeschrieben und umschrieben werden. Die Figur, um die der Kreis beschrieben wird, heißt eingeschrieben, alle ihre Ecken sind Punkte, die auf dem Kreis liegen. Ein umschriebenes Dreieck ist eines, in das ein Kreis einbeschrieben ist. Alle seine Seiten sind an bestimmten Punkten mit ihm in Kontakt.

Wie ist

Die Fläche jeder Figur wird in Quadrateinheiten gemessen (Quadratmeter, Quadratmillimeter, Quadratzentimeter, Quadratdezimeter usw.) Dieser Wert kann je nach Art des Dreiecks auf unterschiedliche Weise berechnet werden. Die Fläche jeder Figur mit Winkeln kann ermittelt werden, indem man ihre Seite mit der aus dem entgegengesetzten Winkel darauf fallenden Senkrechten multipliziert und diese Figur durch zwei teilt. Sie können diesen Wert auch finden, indem Sie die beiden Seiten multiplizieren. Dann multipliziere diese Zahl mit dem Sinus des Winkels zwischen diesen Seiten und teile diese Zahl durch zwei. Wenn Sie alle Seiten eines Dreiecks kennen, aber nicht seine Winkel, können Sie die Fläche auf andere Weise finden. Dazu müssen Sie den halben Umfang finden. Dann subtrahieren Sie abwechselnd verschiedene Seiten von dieser Zahl und multiplizieren Sie die vier erhaltenen Werte. Als nächstes finden Sie die Nummer heraus, die herausgekommen ist. Die Fläche eines einbeschriebenen Dreiecks lässt sich ermitteln, indem man alle Seiten multipliziert und die resultierende Zahl durch die umschriebene Zahl mal vier teilt.

Die Fläche des beschriebenen Dreiecks wird auf diese Weise ermittelt: Wir multiplizieren den halben Umfang mit dem Radius des darin eingeschriebenen Kreises. Wenn dann seine Fläche wie folgt ermittelt werden kann: Wir quadrieren die Seite, multiplizieren die resultierende Zahl mit der Wurzel von drei und teilen diese Zahl dann durch vier. In ähnlicher Weise können Sie die Höhe eines Dreiecks berechnen, in dem alle Seiten gleich sind. Dazu müssen Sie eine davon mit der Wurzel aus drei multiplizieren und diese Zahl dann durch zwei teilen.

Dreieckssätze

Die Hauptsätze, die mit dieser Figur verbunden sind, sind der oben beschriebene Satz des Pythagoras und der Kosinus. Der zweite (Sinus) ist, dass, wenn Sie eine Seite durch den Sinus des ihr gegenüberliegenden Winkels teilen, Sie den Radius des Kreises erhalten können, der darum herum beschrieben wird, multipliziert mit zwei. Der dritte (Kosinus) ist, dass, wenn die Summe der Quadrate der beiden Seiten von ihrem Produkt subtrahiert, mit zwei multipliziert und dem Kosinus des dazwischen liegenden Winkels, das Quadrat der dritten Seite erhalten wird.

Dali-Dreieck – was ist das?

Viele, die mit diesem Konzept konfrontiert sind, denken zunächst, dass dies eine Art Definition in der Geometrie ist, aber das ist überhaupt nicht der Fall. Das Dali-Dreieck ist der gebräuchliche Name für drei Orte, die eng mit dem Leben des berühmten Künstlers verbunden sind. Seine "Spitzen" sind das Haus, in dem Salvador Dali lebte, das Schloss, das er seiner Frau schenkte, und das Museum für surrealistische Gemälde. Bei einem Rundgang durch diese Orte erfahren Sie viel Wissenswertes über diesen weltbekannten, originellen und kreativen Künstler.

Standardnotationen

Dreieck mit Eckpunkten EIN, B und C bezeichnet als (siehe Abb.). Das Dreieck hat drei Seiten:

Die Seitenlängen eines Dreiecks werden durch lateinische Kleinbuchstaben (a, b, c) angegeben:

Das Dreieck hat folgende Winkel:

Die Winkel an den entsprechenden Eckpunkten werden traditionell mit griechischen Buchstaben (α, β, γ) bezeichnet.

Zeichen der Gleichheit von Dreiecken

Ein Dreieck auf der euklidischen Ebene kann eindeutig (bis zur Kongruenz) durch die folgenden Tripletts von Grundelementen definiert werden:

1. a, b, γ (Gleichheit auf zwei Seiten und der dazwischen liegende Winkel);
2. a, β, γ (Seitengleichheit und zwei benachbarte Winkel);
3. a, b, c (Gleichheit auf drei Seiten).

Gleichheitszeichen rechtwinkliger Dreiecke:

1. entlang des Beins und der Hypotenuse;
2. auf zwei Beinen;
3. entlang des Beins und des spitzen Winkels;
4. Hypotenuse und spitzer Winkel.

Einige Punkte im Dreieck sind "gepaart". Beispielsweise gibt es zwei Punkte, von denen aus alle Seiten entweder in einem Winkel von 60° oder in einem Winkel von 120° einsehbar sind. Sie werden gerufen Punkte Torricelli. Es gibt auch zwei Punkte, deren Projektionen an den Seiten an den Ecken eines regelmäßigen Dreiecks liegen. Das - Punkte des Apollonius. Punkte und dergleichen werden genannt Brocard-Punkte.

Direkte

In jedem Dreieck liegen der Schwerpunkt, das Orthozentrum und der Mittelpunkt des umschriebenen Kreises auf derselben Geraden, genannt Euler-Linie.

Die Linie, die durch die Mitte des umschriebenen Kreises und den Lemoine-Punkt verläuft, wird genannt Brokars Achse. Darauf liegen Apollonius-Punkte. Auch die Torricelli-Punkte und der Lemoine-Punkt liegen auf derselben Geraden. Die Basen der äußeren Winkelhalbierenden der Winkel eines Dreiecks liegen auf derselben Geraden, genannt Achse der äußeren Winkelhalbierenden. Die Schnittpunkte der Seitenlinien des Orthodreiecks mit den Seitenlinien des Dreiecks liegen ebenfalls auf derselben Linie. Diese Zeile heißt orthozentrische Achse, sie steht senkrecht auf der Euler-Linie.

Wenn wir einen Punkt auf dem umschriebenen Kreis eines Dreiecks nehmen, liegen seine Projektionen an den Seiten des Dreiecks auf einer geraden Linie, genannt Simsons gerade Linie gegebener Punkt. Simsons Linien von diametral gegenüberliegenden Punkten sind senkrecht.

Dreiecke

• Ein Dreieck mit Eckpunkten an den Basen von Cevianern, die durch einen bestimmten Punkt gezogen werden, wird aufgerufen cevianisches Dreieck dieser Punkt.
• Ein Dreieck mit Ecken in den Projektionen eines gegebenen Punktes auf die Seiten heißt unter der Haut oder Pedaldreieck dieser Punkt.
• Ein Dreieck mit Ecken an den zweiten Schnittpunkten der durch die Ecken gezogenen Linien und dem gegebenen Punkt mit dem umschriebenen Kreis wird aufgerufen cevianisches Dreieck. Ein Cevian-Dreieck ähnelt einem subdermalen Dreieck.

Kreise

• Eingeschriebener Kreis ist ein Kreis, der alle drei Seiten des Dreiecks berührt. Sie ist die Einzige. Der Mittelpunkt des Inkreises wird genannt Im zentrum.
• Umschriebener Kreis- ein Kreis, der durch alle drei Eckpunkte des Dreiecks verläuft. Auch der umschriebene Kreis ist einzigartig.
• Exkreis- ein Kreis, der eine Seite eines Dreiecks tangiert und die Verlängerung der beiden anderen Seiten. In einem Dreieck gibt es drei solcher Kreise. Ihr Radikalzentrum ist das Zentrum des einbeschriebenen Kreises des mittleren Dreiecks, genannt Spiekers Punkt.

Die Mittelpunkte der drei Seiten eines Dreiecks, die Basen seiner drei Höhen und die Mittelpunkte der drei Liniensegmente, die seine Eckpunkte mit dem Orthozentrum verbinden, liegen auf einem einzigen Kreis, der als Dreieck bezeichnet wird Kreis aus neun Punkten oder Eulerscher Kreis. Der Mittelpunkt des Neun-Punkte-Kreises liegt auf der Euler-Linie. Ein Kreis aus neun Punkten berührt einen eingeschriebenen Kreis und drei Exkreise. Der Kontaktpunkt zwischen einem eingeschriebenen Kreis und einem Kreis aus neun Punkten wird genannt Feuerbach Punkt. Wenn wir von jedem Scheitelpunkt aus Dreiecke auf geraden Linien mit Seiten auslegen, Orthesen gleicher Länge wie gegenüberliegende Seiten, dann liegen die resultierenden sechs Punkte auf einem Kreis - Conway kreist. In jedes Dreieck können drei Kreise so eingeschrieben werden, dass jeder von ihnen zwei Seiten des Dreiecks und zwei weitere Kreise berührt. Solche Kreise werden genannt Malfatti-Kreise. Die Mittelpunkte der umschriebenen Kreise der sechs Dreiecke, in die das Dreieck durch Mittellinien unterteilt ist, liegen auf einem Kreis, der als Lamun-Kreis.

Ein Dreieck hat drei Kreise, die zwei Seiten des Dreiecks und den umschriebenen Kreis berühren. Solche Kreise werden genannt halb beschriftet oder Verrier-Kreise. Die Segmente, die die Berührungspunkte der Verrier-Kreise mit dem umschriebenen Kreis verbinden, schneiden sich in einem Punkt, genannt Verrier-Punkt. Er dient als Mittelpunkt der Homothetie, die den umschriebenen Kreis zum Inkreis führt. Die Berührungspunkte der Verrierkreise mit den Seiten liegen auf einer Geraden, die durch den Mittelpunkt des einbeschriebenen Kreises geht.

Die Liniensegmente, die die Tangentenpunkte des einbeschriebenen Kreises mit den Eckpunkten verbinden, schneiden sich in einem Punkt, genannt Gergonne-Punkt, und die Segmente, die die Scheitelpunkte mit den Kontaktpunkten der Exkreise verbinden - in Nagel Punkt.

Ellipsen, Parabeln und Hyperbeln

Eingeschriebener Kegel (Ellipse) und seine Perspektive

Einem Dreieck können unendlich viele Kegelschnitte (Ellipsen, Parabeln oder Hyperbeln) einbeschrieben werden. Wenn wir einem Dreieck einen beliebigen Kegelschnitt einschreiben und die Berührungspunkte mit gegenüberliegenden Eckpunkten verbinden, schneiden sich die resultierenden Linien an einem Punkt, genannt Perspektive Kegel. Für jeden Punkt der Ebene, der nicht auf einer Seite oder auf ihrer Verlängerung liegt, gibt es einen einbeschriebenen Kegelschnitt mit einer Perspektive an diesem Punkt.

Steiners Ellipse umschrieben und Ceviane, die durch ihre Brennpunkte gehen

Eine Ellipse kann in ein Dreieck eingeschrieben werden, das die Seiten in den Mittelpunkten berührt. Eine solche Ellipse heißt Steiner beschriftete Ellipse(seine Perspektive ist der Schwerpunkt des Dreiecks). Die beschriebene Ellipse, die Linien tangiert, die durch Scheitelpunkte parallel zu den Seiten verlaufen, wird aufgerufen umschrieben durch die Steiner-Ellipse. Wenn eine affine Transformation ("Schiefe") das Dreieck in ein reguläres Dreieck übersetzt, dann wird seine eingeschriebene und umschriebene Steiner-Ellipse in einen eingeschriebenen und umschriebenen Kreis übergehen. Cevianer, die durch die Brennpunkte der beschriebenen Steiner-Ellipse (Skutin-Punkte) gezogen werden, sind gleich (Satz von Skutin). Von allen beschriebenen Ellipsen hat die beschriebene Steiner-Ellipse die kleinste Fläche, und von allen eingeschriebenen Ellipsen hat die eingeschriebene Steiner-Ellipse die größte Fläche.

Brocards Ellipse und ihr Perspektor - Lemoine-Punkt

Eine Ellipse mit Brennpunkten an Brokars Punkten wird aufgerufen Brocard-Ellipse. Seine Perspektive ist der Lemoine-Punkt.

Eigenschaften einer einbeschriebenen Parabel

Kiepert-Parabel

Die Perspektiven der eingeschriebenen Parabeln liegen auf der umschriebenen Steiner-Ellipse. Der Fokus einer einbeschriebenen Parabel liegt auf dem umschriebenen Kreis, und die Leitlinie verläuft durch das Orthozentrum. Eine Parabel, die in ein Dreieck eingeschrieben ist, dessen Leitlinie die Euler-Linie ist, wird als Euler-Linie bezeichnet Kiepertsche Parabel. Seine Perspektive ist der vierte Schnittpunkt des umschriebenen Kreises und der umschriebenen Steiner-Ellipse, genannt Steiner Punkt.

Cyperts Übertreibung

Wenn die beschriebene Hyperbel durch den Schnittpunkt der Höhen verläuft, ist sie gleichseitig (dh ihre Asymptoten stehen senkrecht). Der Schnittpunkt der Asymptoten einer gleichseitigen Hyperbel liegt auf einem Kreis aus neun Punkten.

Transformationen

Wenn die Linien, die durch die Scheitelpunkte und einen nicht auf den Seiten liegenden Punkt und ihre Verlängerungen in Bezug auf die entsprechenden Winkelhalbierenden verlaufen, gespiegelt werden, schneiden sich ihre Bilder auch an einem Punkt, der aufgerufen wird isogonal konjugieren die ursprüngliche (wenn der Punkt auf dem umschriebenen Kreis lag, sind die resultierenden Linien parallel). Viele Paare bemerkenswerter Punkte sind isogonal konjugiert: der Mittelpunkt des umschriebenen Kreises und das Orthozentrum, der Schwerpunkt und der Lemoine-Punkt, die Brocard-Punkte. Die Apollonius-Punkte sind isogonal konjugiert zu den Torricelli-Punkten, und das Zentrum des Inkreises ist isogonal konjugiert zu sich selbst. Unter der Wirkung der isogonalen Konjugation gehen gerade Linien in umschriebene Kegelschnitte und umschriebene Kegelschnitte in gerade Linien über. So sind die Kiepert-Hyperbel und die Brocard-Achse, die Enzhabek-Hyperbel und die Euler-Linie, die Feuerbach-Hyperbel und die Mittelpunktslinie des Inkreises isogonal konjugiert. Die umschriebenen Kreise subdermaler Dreiecke isogonal konjugierter Punkte fallen zusammen. Die Brennpunkte der einbeschriebenen Ellipsen sind isogonal konjugiert.

Nimmt man statt eines symmetrischen Cevians ein Cevian, dessen Basis genauso weit von der Seitenmitte entfernt ist wie die Basis des ursprünglichen, so werden sich auch solche Ceviane in einem Punkt schneiden. Die resultierende Transformation wird aufgerufen isotomische Konjugation. Es bildet auch Linien auf umschriebene Kegelschnitte ab. Die Gergonne- und Nagelpunkte sind isotomisch konjugiert. Bei affinen Transformationen gehen isotomisch konjugierte Punkte in isotomisch konjugierte über. Bei der Isotomie-Konjugation geht die beschriebene Steiner-Ellipse in die Gerade im Unendlichen über.

Wenn in die von den Seiten des Dreiecks vom umschriebenen Kreis abgeschnittenen Segmente Kreise eingeschrieben sind, die die Seiten an den Basen der durch einen bestimmten Punkt gezogenen Cevianer berühren, und dann die Berührungspunkte dieser Kreise mit dem umschriebenen verbunden werden Kreis mit gegenüberliegenden Eckpunkten, dann schneiden sich solche Linien in einem Punkt. Die Transformation der Ebene, die den ursprünglichen Punkt an den resultierenden Punkt anpasst, wird aufgerufen isozirkulare Transformation. Die Zusammensetzung der isogonalen und isotomischen Konjugationen ist die Zusammensetzung der isozirkularen Transformation mit sich selbst. Diese Komposition ist eine projektive Transformation, die die Seiten des Dreiecks an Ort und Stelle lässt und die Achse der äußeren Winkelhalbierenden in eine gerade Linie im Unendlichen übersetzt.

Wenn wir die Seiten des Cevian-Dreiecks an einem Punkt fortsetzen und ihre Schnittpunkte mit den entsprechenden Seiten nehmen, liegen die resultierenden Schnittpunkte auf einer geraden Linie, genannt trilinear polar Startpunkt. Orthozentrische Achse - trilinearer Pol des Orthozentrums; die trilineare Polare des Zentrums des einbeschriebenen Kreises ist die Achse der äußeren Winkelhalbierenden. Die trilinearen Polare der auf dem umschriebenen Kegelschnitt liegenden Punkte schneiden sich in einem Punkt (beim umschriebenen Kreis ist dies der Lemoine-Punkt, bei der umschriebenen Steiner-Ellipse der Schwerpunkt). Die Zusammensetzung der isogonalen (oder isotomischen) Konjugation und der trilinearen Polarität ist eine Dualitätstransformation (wenn der Punkt isogonal (isotomisch) konjugiert zum Punkt liegt, dann liegt die trilineare Polarität des Punktes isogonal (isotomisch) konjugiert zum Punkt liegt auf der trilinearen Polare des Punktes ).

Würfel

Beziehungen in einem Dreieck

Notiz: dabei sind , , die Längen der drei Seiten des Dreiecks und , , die diesen drei Seiten jeweils gegenüberliegenden Winkel (Gegenwinkel).

Dreiecksungleichung

Bei einem nicht entarteten Dreieck ist die Summe der Längen seiner beiden Seiten größer als die Länge der dritten Seite, bei einem entarteten Dreieck ist sie gleich. Mit anderen Worten, die Längen der Seiten eines Dreiecks hängen durch die folgenden Ungleichungen zusammen:

Die Dreiecksungleichung ist eines der Axiome der Metrik.

Dreieckswinkelsummensatz

Sinussatz

wobei R der Radius des um das Dreieck umschriebenen Kreises ist. Aus dem Satz folgt, dass wenn a< b < c, то α < β < γ.

Kosinussatz

Tangentensatz

Andere Verhältnisse

Metrische Verhältnisse in einem Dreieck sind angegeben für:

Dreiecke lösen

Die Berechnung unbekannter Seiten und Winkel eines Dreiecks auf der Grundlage bekannter Seiten wurde historisch als "Dreieckslösungen" bezeichnet. In diesem Fall werden die obigen allgemeinen trigonometrischen Theoreme verwendet.

Fläche eines Dreiecks

Für die Fläche gelten folgende Ungleichungen:

Berechnung der Fläche eines Dreiecks im Raum mit Vektoren

Die Eckpunkte des Dreiecks seien an den Punkten , , .

Wir führen den Flächenvektor ein. Die Länge dieses Vektors entspricht der Fläche des Dreiecks und ist entlang der Normalen zur Ebene des Dreiecks gerichtet:

Seien , wobei , , die Projektionen des Dreiecks auf die Koordinatenebenen sind. Dabei

und ebenfalls

Die Fläche des Dreiecks ist .

Eine Alternative besteht darin, die Seitenlängen (mit dem Satz des Pythagoras) zu berechnen und dann die Heron-Formel zu verwenden.

Dreieckssätze

Dreieck . Spitze, stumpfe und rechtwinklige Dreiecke.

Die Beine und die Hypotenuse. Gleichschenkliges und gleichseitiges Dreieck.

Die Summe der Winkel eines Dreiecks.

Die äußere Ecke des Dreiecks. Zeichen der Gleichheit von Dreiecken.

Wunderbare Linien und Punkte in einem Dreieck: Höhen, Seitenhalbierende,

Winkelhalbierende, Median e Senkrechte, Orthozentrum,

Schwerpunkt, Mittelpunkt des umschriebenen Kreises, Mittelpunkt des einbeschriebenen Kreises.

Satz des Pythagoras. Das Seitenverhältnis eines beliebigen Dreiecks.

Dreieck ist ein Polygon mit drei Seiten (oder drei Ecken). Die Seiten eines Dreiecks werden oft mit kleinen Buchstaben bezeichnet, die den Großbuchstaben entsprechen, die gegenüberliegende Ecken bezeichnen.

Wenn alle drei Winkel spitz sind ( Abb. 20), dann dies spitzwinkliges Dreieck . Wenn eine der Ecken stimmt(C, Abb.21), das ist rechtwinkliges Dreieck; Seitenein, beinen rechten Winkel bilden, nennt man Beine; SeiteCgegenüber dem rechten Winkel heißt Hypotenuse. Wenn einer von stumpfe Winkel ( B, Abb.22), das ist Stumpfes Dreieck.


Dreieck ABC (Abb. 23) - gleichschenklig, wenn zwei seine Seiten sind gleichein= C); diese gleichen Seiten heißen seitlich, wird der Dritte angerufen Basis Dreieck. Dreieck ABC (Abb. 24) - gleichseitig, wenn alle seine Seiten sind gleichein = B = C). Im Allgemeinen ( ein ≠ B ≠ C) wir haben skaliert Dreieck .

Grundlegende Eigenschaften von Dreiecken. In jedem Dreieck:

1. Der größeren Seite steht ein größerer Winkel gegenüber und umgekehrt.

2. Gleichen Winkeln liegen gleiche Seiten gegenüber und umgekehrt.

Insbesondere alle Winkel in gleichseitig Dreieck sind gleich.

3. Die Summe der Winkel eines Dreiecks ist 180 º .

Aus den letzten beiden Eigenschaften folgt, dass jeder Winkel gleichseitig ist

Dreieck ist 60 º.

4. Fortsetzung einer der Seiten des Dreiecks (AC, Abb. 25), wir bekommen extern

Winkel BCD . Der Außenwinkel eines Dreiecks ist gleich der Summe der Innenwinkel,

nicht damit verwandt :BCD=A+B.

5. Beliebig Seite eines Dreiecks ist kleiner als die Summe der beiden anderen Seiten und mehr

ihre Unterschiede (ein < B + C, ein > B – C;B < ein + C, B > ein – C;C < ein + B,C > ein – B).

Zeichen der Gleichheit von Dreiecken.

Dreiecke sind kongruent, wenn sie jeweils gleich sind:

ein ) zwei Seiten und der Winkel zwischen ihnen;

B ) zwei Ecken und die daran angrenzende Seite;

c) drei Seiten.

Zeichen der Gleichheit rechtwinkliger Dreiecke.

Zwei rechteckig Dreiecke sind kongruent, wenn eine der folgenden Bedingungen zutrifft:

1) ihre Beine sind gleich;

2) das Bein und die Hypotenuse eines Dreiecks sind gleich dem Bein und der Hypotenuse des anderen;

3) die Hypotenuse und der spitze Winkel eines Dreiecks sind gleich der Hypotenuse und dem spitzen Winkel des anderen;

4) das Bein und der angrenzende spitze Winkel eines Dreiecks sind gleich dem Bein und dem angrenzenden spitzen Winkel des anderen;

5) das Bein und der gegenüberliegende spitze Winkel eines Dreiecks sind gleich dem Bein und gegenüber dem spitzen Winkel des anderen.

Wunderbare Linien und Punkte in einem Dreieck.

Höhe Dreieck istaufrecht,von jedem Scheitelpunkt auf die gegenüberliegende Seite fallen gelassen ( oder seine Fortsetzung). Diese Seite heißtdie Basis des Dreiecks . Die drei Höhen eines Dreiecks schneiden sich immeran einer Stellenamens Orthozentrum Dreieck. Das Orthozentrum eines spitzen Dreiecks (PunktÖ , Abb. 26) befindet sich innerhalb des Dreiecks undOrthozentrum eines stumpfen Dreiecks (PunktÖ , Abb.27) – außen; Der Orthomittelpunkt eines rechtwinkligen Dreiecks fällt mit der Spitze des rechten Winkels zusammen.

Median - Das Sektion , die jeden Eckpunkt eines Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet. Drei Seitenhalbierende eines Dreiecks (AD , BE , CF , Abb.28) schneiden sich in einem Punkt Ö , die immer innerhalb des Dreiecks liegt und sein sein Schwerpunkt. Dieser Punkt teilt jeden Median 2:1 von oben.

Bisektor - Das halbierendes Segment Ecke von oben nach oben Schnittpunkt mit der Gegenseite. Drei Winkelhalbierende eines Dreiecks (AD , BE , CF , Abb.29) schneiden sich in einem Punkt Oh, immer in einem Dreieck liegen und Sein eingeschriebener Kreismittelpunkt(siehe Abschnitt „Beschriftetund umschriebene Polygone).

Die Winkelhalbierende teilt die gegenüberliegende Seite in Teile, die proportional zu den angrenzenden Seiten sind ; zum Beispiel in Abb. 29 AE : CE = AB : BC .

Mittlere Senkrechte ist eine vom Mittelwert gezogene Senkrechte Segmentpunkte (Seiten). Drei senkrechte Winkelhalbierende des Dreiecks ABC(KO , MO , NO , Abb.30 ) schneiden sich in einem Punkt O, das ist Center umschriebener Kreis (Punkte K , M , N die Mittelpunkte der Seiten eines Dreiecks ABC).

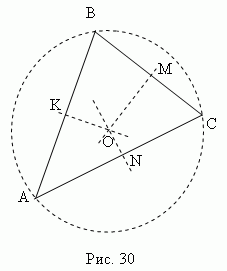
In einem spitzwinkligen Dreieck liegt dieser Punkt innerhalb des Dreiecks; in stumpf - draußen; im Rechteck - in der Mitte der Hypotenuse. Orthozentrum, Schwerpunkt, Mittelpunkt des umschriebenen Kreises und Mittelpunkt des einbeschriebenen Kreises fallen nur in einem gleichseitigen Dreieck zusammen.

Satz des Pythagoras. In einem rechtwinkligen Dreieck das Quadrat der LängeDie Hypotenuse ist gleich der Summe der Quadrate der Beinlängen.

Der Beweis des Satzes von Pythagoras folgt offensichtlich aus Abb.31. Betrachten Sie ein rechtwinkliges Dreieck ABC mit Beinen ein, b und Hypotenuse C.

Lass uns ein Quadrat bauen AKMB unter Verwendung der Hypotenuse AB als Seite. DannVerlängern Sie die Seiten eines rechtwinkligen Dreiecks ABC also um ein quadrat zu bekommen CDEF , dessen Seite gleich ista+b.Nun ist klar, dass die Fläche ein Quadrat ist CDEF ist ( a+b) 2 . Andererseits diese die Fläche ist gleich der Summe Bereiche vier rechtwinklige dreiecke und Quadrat AKMB , das heißt

C 2 + 4 (ab / 2) = C 2 + 2 ab,

von hier,

C 2 + 2 ab= (a+b) 2 ,

und schließlich haben wir:

C 2 =ein 2 +b 2 .

Das Seitenverhältnis eines beliebigen Dreiecks.

Im allgemeinen Fall (für ein beliebiges Dreieck) gilt:

C 2 =ein 2 +b 2 – 2ab· cos C,

wo C - Winkel zwischen den Seitenein und B .

Wie heißen die Winkel eines Dreiecks? Die Antwort kann davon abhängen, wie viele Ecken sich an der Spitze des Dreiecks befinden.

Wenn ein Dreieck nur einen Winkel hat, kann es mit einem Buchstaben nach dem Namen des Scheitelpunkts bezeichnet werden.

Beispielsweise hat im Dreieck MKF (Abbildung 1) jede Ecke nur einen Winkel. Daher kann jede der Ecken mit einem Buchstaben bezeichnet werden, mit dem Namen des Scheitelpunkts, von dem die Strahlen ausgehen, die diese Ecke bilden:

Bild 1

M-Winkel, K-Winkel und F-Winkel.

Es gibt ein spezielles Zeichen, um einen Winkel zu bezeichnen: ∠

Die Notation ∠M wird als "Winkel M" gelesen.

Jede der Ecken des Dreiecks MKF kann auch als drei Buchstaben bezeichnet werden. In diesem Fall sollte der Scheitelpunkt im Namen der Ecke in der Mitte liegen.

Winkel M kann auch als Winkel KMF oder Winkel FMK bezeichnet werden,

∠K - ∠MKF oder ∠FKM,

∠F - ∠MFK oder ∠KFM.

Figur 2

In den in Abbildung 2 gezeigten Dreiecken können nur die Winkel an den Eckpunkten A und D mit einem Buchstaben benannt werden: ∠A und ∠D.

Es gibt drei Ecken am Scheitelpunkt B, also muss jede dieser Ecken mit drei Buchstaben benannt werden: ∠ABC, ∠CBD und ∠ABD.

Ebenso können Scheitelecken C nur mit drei Buchstaben benannt werden: ∠ACB, ∠BCD und ∠ACD. Es ist unmöglich, einen dieser Winkel ∠C zu nennen.

Figur 3

Jede der Ecken der in Abbildung 3 gezeigten Dreiecke kann nur mit drei Buchstaben benannt werden.

Winkel des Dreiecks ABO: ∠ABO, ∠BAO, ∠AOB.

Winkel des Dreiecks BOC: ∠BOC, ∠OBC, ∠BCO.

Winkel des Dreiecks OCD: ∠OCD, ∠COD, ∠CDO.

Winkel des Dreiecks AOD: ∠AOD, ∠ADO, ∠OAD.

Winkel des Dreiecks ABC: ∠ABC, ∠BAC, ∠BCA.

Winkel des Dreiecks BCD: ∠BCD, ∠CBD, ∠BDC.

Winkel des Dreiecks ACD: ∠ACD, ∠CAD, ∠ADC.

Winkel des Dreiecks ABD: ∠ABD, ∠BAD, ∠ADB.