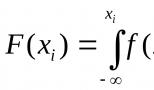Одной плоскости имеют общую. Три различные плоскости имеют общую точку. Вернр ли, что данные плоскости имеют общую прямую? Объясните. Взаимное расположение плоскостей
Аксиомы стереометрии.
А1.Через любые три точки, не лежащие на данной прямой, проходит плоскость, и притом только одна;
Сл.1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна;
Сл.2. Через две пересекающиеся прямые проходит плоскость, и притом только одна;
Сл.3. Через две параллельные прямые проходит плоскость, и притом только одна.
А2.Если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости ;
А3.Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Основные фигуры стереометрии – точки (А, В, С…) , прямые (а, b, c…) , плоскости ( …) , многогранники и тела вращения.
Под секущей плоскостью объемной фигуры будем понимать плоскость, по обе стороны которой имеются точки данной фигуры.
За меру расстояния между точкой, прямой и плоскостью будем принимать длину их общего перпендикуляра.
2. Взаимное расположение прямых в пространстве.
В пространстве две прямые могут быть параллельными, пересекаться или скрещиваться .
| 1А | Опр.Параллельными прямыми в пространстве называются прямые, которые лежат в одной плоскости и не пересекаются. По сл. 3.Через две параллельные прямые проходит плоскость, и притом только одна. | |
| 1Б | Т 1 (о транзитивности). Две прямые, параллельные третьей, параллельны между собой. | |
| 2А | По сл.2.Через две пересекающиеся прямые проходит плоскость, и притом только одна | |
| 3А | Опр. Две прямые называются скрещивающимися , если они не лежат в одной плоскости. | |
| Т 2 (Признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то такие прямые являются скрещивающимися. | ||
| 3Б | Опр.Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми. | |
| 3В | Опр. Общим перпендикуляром двух скрещивающихся прямых называется отрезок, имеющий концы на данных прямых и перпендикулярный к ним (расстояние между скрещивающимися прямыми). |
- Взаимное расположение прямых и плоскостей в пространстве.
В пространстве прямая и плоскость могут быть параллельными, пересекаться или прямая целиком может лежать в плоскости .
| 1А | Опр.Прямая называется параллельной плоскости , если она параллельна любой прямой, лежащей в этой плоскости. | |
| 1Б | Т 3 (Признак параллельности прямой и плоскости) . Прямая, не лежащая в плоскости, параллельна плоскости, если она параллельна какой-нибудь прямой лежащей в этой плоскости. | |
| 2А | Опр. Прямая называется перпендикулярной плоскости , если она перпендикулярна к любой пересекающимся прямым, лежащим в этой плоскости. | |
| 2Б | Т 4 (признак перпендикулярности прямой и плоскости) Если прямая, пересекающая с плоскость, перпендикулярна к каким-нибудь двум пересекающимся прямым, лежащим в этой плоскости, то она перпендикулярна и ко всякой третьей прямой лежащей в этой плоскости. | |
| 2В | Т 5 (о двух параллельных прямых, перпендикулярных третьей). Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости. | |
| 2Г | Опр. Углом между прямой и плоскостью называется угол, между данной прямой и её проекцией на плоскость. | |
| 2Д | Опр.Всякая иная прямая, отличная от перпендикуляра и пересекающая плоскость, называется наклонной к этой плоскости (рис. см. ниже). Опр.Проекцией наклонной на плоскость называется отрезок, соединяющий основание перпендикуляра и наклонной. Т 6 (о длине перпендикуляра и наклонной). 1) Перпендикуляр, проведённый к плоскости короче наклонной к этой плоскости; 2) Равным наклонным соответствуют равные проекции; 3) Из двух наклонных больше та, проекция которой больше. | |
| 2Е | Т 7 (о трёх перпендикулярах). Прямая, проведённая на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и самой наклонной. Т 8 (обратная). Прямая, проведённая на плоскости через основание наклонной и перпендикулярно ей, перпендикулярна и проекции наклонной на данню плоскость. | |
| 3А | По аксиоме 2.Если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости |
- Взаимное расположение плоскостей в пространстве.
В пространстве плоскости могут быть параллельными или пересекаться.
| 1А | Опр. Две плоскости называются параллельными , если они не пересекаются. | |
| Т 9 (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. | ||
| 1Б | Т 10 Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения параллельны (свойство параллельных плоскостей 1). | |
| 1В | Т 11 Отрезки параллельных прямых, заключенных между параллельными плоскостями, равны (свойство параллельных плоскостей 2). | |
| 2А | По аксиоме 3 . Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (плоскости пересекаются по прямой ). | |
| 2Б | Т 12 (признак перпендикулярности плоскостей). Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. | |
| 2В | Опр.Двугранным углом называется фигура, образованная двумя полуплоскостями, исходящими из одной прямой. Плоскость, перпендикулярная ребру двугранного угла, пересекает его грани по двум лучам. Угол, образованный этими лучами называется линейным углом двугранного угла. За меру двугранного угла принимается мера соответствующего ему линейного угла. |
В планиметрии плоскость является одной из основных фигур, поэтому, очень важно иметь ясное представление о ней. Эта статья создана с целью раскрытия этой темы. Сначала дано понятие плоскости, ее графическое представление и показаны обозначения плоскостей. Далее плоскость рассматривается вместе с точкой, прямой или другой плоскостью, при этом возникают варианты из взаимного расположения в пространстве. Во втором и третьем и четвертом пункте статьи как раз разобраны все варианты взаимного расположения двух плоскостей, прямой и плоскости, а также точки и плоскости, приведены основные аксиомы и графические иллюстрации. В заключении даны основные способы задания плоскости в пространстве.
Навигация по странице.
Плоскость – основные понятия, обозначения и изображение.
Простейшими и основными геометрическими фигурами в трехмерном пространстве являются точка, прямая и плоскость. Мы уже имеем представление о точке и прямой на плоскости . Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.
Точки и прямые в пространстве обозначаются также как и на плоскости – большими и маленькими латинскими буквами соответственно. Например, точки А и Q , прямые а и d . Если заданы две точки, лежащие на прямой, то прямую можно обозначить двумя буквами, соответствующими этим точкам. К примеру, прямая АВ или ВА проходит через точки А и В . Плоскости принято обозначать маленькими греческими буквами, например, плоскости , или .
При решении задач возникает необходимость изображать плоскости на чертеже. Плоскость обычно изображают в виде параллелограмма или произвольной простой замкнутой области.

Плоскость обычно рассматривается вместе с точками, прямыми или другими плоскостями, при этом возникают различные варианты их взаимного расположения. Переходим к их описанию.
Взаимное расположение плоскости и точки.
Начнем с аксиомы: в каждой плоскости имеются точки. Из нее следует первый вариант взаимного расположения плоскости и точки – точка может принадлежать плоскости. Другими словами, плоскость может проходить через точку. Для обозначения принадлежности какой-либо точки какой-либо плоскости используют символ «». Например, если плоскость проходит через точку А , то можно кратко записать .
Следует понимать, что на заданной плоскости в пространстве имеется бесконечно много точек.
Следующая аксиома показывает, сколько точек в пространстве необходимо отметить, чтобы они определяли конкретную плоскость: через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. Если известны три точки, лежащие в плоскости, то плоскость можно обозначить тремя буквами, соответствующими этим точкам. Например, если плоскость проходит через точки А , В и С , то ее можно обозначить АВС .
Сформулируем еще одну аксиому, которая дает второй вариант взаимного расположения плоскости и точки: имеются по крайней мере четыре точки, не лежащие в одной плоскости. Итак, точка пространства может не принадлежать плоскости. Действительно, в силу предыдущей аксиомы через три точки пространства проходит плоскость, а четвертая точка может как лежать на этой плоскости, так и не лежать. При краткой записи используют символ «», который равносилен фразе «не принадлежит».
К примеру, если точка А не лежит в плоскости , то используют краткую запись .

Прямая и плоскость в пространстве.
Во-первых, прямая может лежать в плоскости. В этом случае, в плоскости лежат хотя бы две точки этой прямой. Это устанавливается аксиомой: если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. Для краткой записи принадлежности некоторой прямой данной плоскости пользуются символом «». Например, запись означает, что прямая а лежит в плоскости .

Во-вторых, прямая может пересекать плоскость. При этом прямая и плоскость имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости. При краткой записи пересечение обозначаю символом «». К примеру, запись означает, что прямая а пересекает плоскость в точке М . При пересечении плоскости некоторой прямой возникает понятие угла между прямой и плоскостью .

Отдельно стоит остановиться на прямой, которая пересекает плоскость и перпендикулярна любой прямой, лежащей в этой плоскости. Такую прямую называют перпендикулярной к плоскости. Для краткой записи перпендикулярности используют симовл «». Для более глубокого изучения материала можете обратиться к статье перпендикулярность прямой и плоскости .

Особую значимость при решении задач, связанных с плоскостью, имеет так называемый нормальный вектор плоскости . Нормальным вектором плоскости является любой ненулевой вектор, лежащий на прямой, перпендикулярной этой плоскости.

В-третьих, прямая может быть параллельна плоскости, то есть, не иметь в ней общих точек. При краткой записи параллельности используют символ «». Например, если прямая а параллельна плоскости , то можно записать . Рекомендуем подробнее изучить этот случай, обратившись к статье параллельность прямой и плоскости .

Следует сказать, что прямая, лежащая в плоскости, делит эту плоскость на две полуплоскости. Прямая в этом случае называется границей полуплоскостей. Любые две точки одной полуплоскости лежат по одну сторону от прямой, а две точки разных полуплоскостей лежат по разные стороны от граничной прямой.
Взаимное расположение плоскостей.
Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.
Две плоскости в пространстве могут пересекаться. Пересечением двух плоскостей является прямая линия, что устанавливается аксиомой: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае возникает понятие угла между пересекающимися плоскостями . Отдельный интерес представляет случай, когда угол между плоскостями равен девяноста градусам. Такие плоскости называют перпендикулярными. О них мы поговорили в статье перпендикулярность плоскостей .
Наконец, две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек. Рекомендуем ознакомиться со статьей параллельность плоскостей , чтобы получить полное представление об этом варианте взаимного расположения плоскостей.

Способы задания плоскости.
Сейчас мы перечислим основные способы задания конкретной плоскости в пространстве.
Во-первых, плоскость можно задать, зафиксировав три не лежащие на одной прямой точки пространства. Этот способ основан на аксиоме: через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
Если в трехмерном пространстве зафиксирована и задана плоскость с помощью указания координат трех ее различных точек, не лежащих на одной прямой, то мы можем написать уравнение плоскости, проходящей через три заданные точки .

Два следующих способа задания плоскости являются следствием из предыдущего. Они основаны на следствиях из аксиомы о плоскости, проходящей через три точки:
- через прямую и не лежащую на ней точку проходит плоскость, притом только одна (смотрите также статью уравнение плоскости, проходящей через прямую и точку);
- через две пересекающиеся прямые проходит единственная плоскость (рекомендуем ознакомиться с материалом статьи уравнение плоскости, проходящей через две пересекающиеся прямые).


Четвертый способ задания плоскости в пространстве основан на определении параллельных прямых . Напомним, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Таким образом, указав две параллельные прямые в пространстве, мы определим единственную плоскость, в которой эти прямые лежат.
Если в трехмерном пространстве относительно прямоугольной системы координат задана плоскость указанным способом, то мы можем составить уравнение плоскости, проходящей через две параллельные прямые .


В курсе средней школы на уроках геометрии доказывается следующая теорема: через фиксированную точку пространства проходит единственная плоскость, перпендикулярная к данной прямой. Таким образом, мы можем задать плоскость, если укажем точку, через которую она проходит, и прямую, перпендикулярную к ней.
Если в трехмерном пространстве зафиксирована прямоугольная система координат и задана плоскость указанным способом, то можно составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой .

Вместо прямой, перпендикулярной к плоскости, можно указать один из нормальных векторов этой плоскости. В этом случае есть возможность написать
Тема «Аксиомы стереометрии и следствия из них». Вариант 2 . 1.Что можно сказать о взаимном расположении двух плоскостей, которые имеют три общиеточки, не лежащие на одной прямой? а) Пересекаются; б) ничего сказать нельзя; в) не пересекаются; г) совпадают; д) имеют три общие точки.
2. Какое из следующих утверждений верно? а) Если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; б) прямая, лежащая в плоскости треугольника, пересекает две его стороны; в) любые две плоскости имеют только одну общую точку; г) через две точки проходит плоскость и притом только одна; д) прямая лежит в плоскости данного треугольника, если она пересекает две прямые, содержащие стороны треугольника.
3. Могут ли две различные плоскости иметь только две общие точки? а) Никогда; б) могу, но при дополнительных условиях; в) всегда имеют; г) нельзя ответить на вопрос; д) другой ответ.
4. Точки K, L, M лежат на одной прямой, точка N не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось? а) 1; б) 2; в) 3; г) 4; д) бесконечно много.
5. Выберите верное утверждение. а) Через любые три точки проходит плоскость, и притом только одна; б) если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости; в) если две плоскости имеют общую точку, то они не пересекаются; г) через прямую и точку, лежащую на ней, проходит плоскость, и притом только одна; д) через две пересекающиеся прямые плоскость провести нельзя.
6. Назовите общую прямую плоскостей PBM и MAB. а) PM; б) AB; в) PB; г) BM; д) определить нельзя.
7. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Что можно сказать о взаимном положении прямых а, b и c? а) Все прямые лежат в разных плоскостях; б) прямые а и b лежат в одной плоскости; в) все прямые лежат в одной плоскости; г) ничего сказать нельзя; д) прямая с совпадает с одной из прямых: или с а, или с b.
8. Прямые а и b пересекаются в точке О. A € a, B € b, Y € AB. Выберите верное утверждение. а) Точки O и Y не лежат в одной плоскости; б) прямые OY и a параллельны; в) прямые a, b и точка Y лежат в одной плоскости; г) точки O и Y совпадают; д) точки Y и A совпадают.
Вариант 2.1.Что можно сказать о взаимном расположении двух плоскостей, которые имеют три общие точки, не лежащие на одной прямой?
а) Пересекаются; б) ничего сказать нельзя; в) не пересекаются; г) совпадают; д) имеют три общие точки.
2. Какое из следующих утверждений верно?
а) Если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; б) прямая, лежащая в плоскости треугольника, пересекает две его стороны; в) любые две плоскости имеют только одну общую точку; г) через две точки проходит плоскость и притом только одна; д) прямая лежит в плоскости данного треугольника, если она пересекает две прямые, содержащие стороны треугольника.
3. Могут ли две различные плоскости иметь только две общие точки?
а) Никогда; б) могу, но при дополнительных условиях; в) всегда имеют; г) нельзя ответить на вопрос; д) другой ответ.
4. Точки K, L, M лежат на одной прямой, точка N не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось?
а) 1; б) 2; в) 3; г) 4; д) бесконечно много.
5. Выберите верное утверждение.
а) Через любые три точки проходит плоскость, и притом только одна; б) если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости; в) если две плоскости имеют общую точку, то они не пересекаются; г) через прямую и точку, лежащую на ней, проходит плоскость, и притом только одна; д) через две пересекающиеся прямые плоскость провести нельзя.
6. Назовите общую прямую плоскостей PBM и MAB.
а) PM; б) AB; в) PB; г) BM; д) определить нельзя.
7. Какую из перечисленных плоскостей пересекает прямая РМ (рис.1)?
а) DD1C; б) D1PM; в) B1PM; г) ABC; д) CDA.
В1 С1
8.Две плоскости пересекаются по прямой с. Точка М лежит только в одной из плоскостей. Что можно сказать о взаимном положении точки М и прямой с?
а) Никакого вывода сделать нельзя; б) прямая с проходит через точку М; в) точка М лежит на прямой с; г) прямая с не проходит через точку М; д) другой ответ.
9. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Что можно сказать о взаимном положении прямых а, b и c?
а) Все прямые лежат в разных плоскостях; б) прямые а и b лежат в одной плоскости; в) все прямые лежат в одной плоскости; г) ничего сказать нельзя; д) прямая с совпадает с одной из прямых: или с а, или с b.
10. Прямые а и b пересекаются в точке О. A € a, B € b, Y € AB. Выберите верное утверждение.
а) Точки O и Y не лежат в одной плоскости; б) прямые OY и a параллельны; в) прямые a, b и точка Y лежат в одной плоскости; г) точки O и Y совпадают; д) точки Y и A совпадают.
лучи АВ и АС перпендикулярны его ребру? 2.Верно ли, что линейный угол ВАС двугранного угла, если лучи АВ и АС лежат в гранях двугранного угла? 3. Верно ли, что угол ВАС - линейный угол двугранного угла, если лучи АВ и АС перпендекулярны его ребру, а точки Е и С лежат на гранях угла? 4. Линейный угол двугранного угла равен 80 градусов. Найдется ли в одной из граней угла прямая, перпендикулярная другой грани? 5. Угол АВС - линейный угол двугранного угла с ребром альфа. Перпендекулярна ли прямая альфа плоскости АВС? Верно ли, что все прямые, перпендекулярные данной плоскости и пересекающие данную прямую, лежат в одной плоскости.
Три плоскости могут не иметь ни одной общей точки (если по крайней мере две из них параллельны, а также если прямые их пересечения параллельны), могут иметь бесчисленное множество общих точек (если все они проходят через одну прямую) или иметь только
одну общую точку. В первом случае система уравнений
не имеет решений, во втором имеет бесчисленное множество решений, в третьем - только одно решение. Для исследования удобнее всего применить определители (§ 183, 190), но можно обойтись и средствами элементарной алгебры.
Пример 1. Плоскости

не имеют общих точек, так как плоскости (1) и (2) параллельны (§ 125). Система уравнений несовместна (уравнения (1) и (2) противоречат друг другу).
Пример 2. Исследовать, есть ли общие точки у трех плоскостей

Ищем решение системы (4)-(6). Исключив 2 из (4) и (5), получаем исключив 2 из (4) и (6), получаем Эти два уравнения несовместны. Значит, три плоскости не имеют общих точек. Так как среди них нет параллельных плоскостей, то три прямые, по которым плоскости попарно пересекаются, параллельны.
Пример 3. Исследовать, есть ли общие точки у плоскостей
Поступая, как в примере 2, получим оба раза т. е. фактически не два, а одно уравнение. Оно имеет бесчисленное множество решений. Значит, три