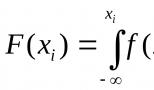Использование л. Амплитудно-фазовая характеристика (годограф Найквиста) Использование л.а.ч.х. и фазовых частотных характеристик для анализа устойчивости системы

Это геометрическое место точек, которые описывает конец вектора частотной передаточной функции, при изменении частоты от -∞ до +∞. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка.

От АФХ порождаются все другие частотные зависимости:

U (w) - четная (для замкнутых САР P (w));
V (w) - нечетная;
A (w) - четная (АЧХ);
j(w) - нечетная (ФЧХ);
ЛАЧХ & ЛФЧХ - используются наиболее часто.

Логарифмические частотные характеристики.

Логарифмические частотные характеристики (ЛЧХ) включают в себя построенные отдельно на одной плоскости логарифмическую амплитудную характеристику (ЛАЧХ) и логарифмическую фазовую характеристику (ЛФЧХ). Построение ЛАЧХ & ЛФЧХ производится по выражениям:

L (w) = 20 lg |W (j w)| = 20 lg A (w), [дБ];

j(w) = arg(W (j w)), [рад].

Величина L (w) выражается в децибелах . Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один Бел соответствует увеличению мощности в 10 раз, 2 Бела – в 100 раз, 3 Бела – в 1000 раз и т.д. Децибел равен одной десятой части Бела.

Примеры АФЧХ, АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ для типовых динамических звеньев приведены в таблице 2.

Таблица 2. Частотные характеристики типовых динамических звеньев.

Принципы автоматического регулирования

По принципу управления САУ можно разбить на три группы:

С регулированием по внешнему воздействию - принцип Понселе (применяется в незамкнутых САУ).
С регулированием по отклонению - принцип Ползунова-Уатта (применяется в замкнутых САУ).
С комбинированным регулированием. В этом случае САУ содержит замкнутый и разомкнутый контуры регулирования.

Принцип управления по внешнему возмущению

В структуре обязательны датчики возмущения. Система описывается передаточной функцией разомкнутой системы: x (t ) = g (t ) - f (t ).

Достоинства:

Можно добиться полной инвариантности к определенным возмущениям.
Не возникает проблема устойчивости системы, т.к. нет ОС.

Недостатки:

Большое количество возмущений требует соответствующего количества компенсационных каналов.
Изменения параметров регулируемого объекта приводят к появлению ошибок в управлении.
Можно применять только к тем объектам, чьи характеристики четко известны.

Принцип управления по отклонению

Система описывается передаточной функцией разомкнутой системы и уравнением замыкания: x (t ) = g (t ) - y (t ) W oc (t ). Алгоритм работы системы заключен в стремлении свести ошибку x (t ) к нулю.

Достоинства:

ООС приводит к уменьшению ошибки не зависимо от факторов ее вызвавших (изменений параметров регулируемого объекта или внешних условий).

Недостатки:

В системах с ОС возникает проблема устойчивости.
В системах принципиально невозможно добиться абсолютной инвариантности к возмущениям. Стремление добиться частичной инвариантности (не 1-ыми ОС) приводит к усложнению системы и ухудшению устойчивости.

Комбинированное управление

Комбинированное управление заключено в сочетании двух принципов управления по отклонению и внешнему возмущению. Т.е. сигнал управления на объект формируется двумя каналами. Первый канал чувствителен к отклонению регулируемой величины от задания. Второй формирует управляющее воздействие непосредственно из задающего или возмущающего сигнала.

x (t ) = g (t ) - f (t ) - y (t )Woc (t )

Достоинства:

Наличие ООС делает систему менее чувствительной к изменению параметров регулируемого объекта.
Добавление канала(ов), чувствительного к заданию или к возмущению, не влияет на устойчивость контура ОС.

Недостатки:

Каналы, чувствительные к заданию или к возмущению, обычно содержат дифференцирующие звенья. Их практическая реализация затруднена.
Не все объекты допускают форсирование.

Анализ устойчивости САР

Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Устойчивость является одним из главных требований, предъявляемых к автоматическим системам.

Понятие устойчивости можно распространить и на случай движения САР:

невозмущенное движение,
возмущенное движение.

Движение любой СУ описывается с помощью дифференциального уравнения, которое в общем случае описывает 2 режима работы системы:

Режим установившегося состояния

Режим движения

При этом общее решение в любой системе можно записать в виде:

Вынужденная составляющая определяется входным воздействием на вход СУ. Этого состояния система достигает по окончании переходных процессов.

Переходная составляющая определяется решением однородного дифференциального уравнения вида:

Коэффициенты a 0 ,a 1 ,…a n включают в себя параметры системы => изменение любого коэффициента дифференциального уравнения приводит к изменению целого ряда параметров системы.

Решение однородного дифференциального уравнения

где постоянные интегрирования, а – корни характеристического уравнения следующего вида:

Характеристическое уравнение представляет собой знаменатель передаточной функции приравненный к нулю.

Корни характеристического уравнения могут быть вещественными, комплексно-сопряженными и комплексными, что определяется параметрами системы.

Чтобы оценивать устойчивость систем, разработан ряд критериев устойчивости

Все критерии устойчивости делятся на 3 группы:

Корневые

- алгебраические

Критерий устойчивости Найквиста сформулирован и обоснован в 1932 году американским физиком Х. Найквистом. Критерий устойчивости Найквиста наиболее широко используется в инженерной практике по следующим причинам:

- устойчивость системы в замкнутом состоянии исследуют по частотной передаточной функции ее разомкнутой части W p (jw), а эта функция, чаще всего, состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из условий устойчивости;

- для исследования устойчивости можно использовать экспериментально полученные частотные характеристики наиболее сложных элементов системы (объекта управления, исполнительных органов), что повышает точность полученных результатов;

- устойчивость системы можно исследовать по логарифмическим частотным характеристикам, построение которых не сложно;

- достаточно просто определяются запасы устойчивости системы;

- удобно использовать для оценки устойчивости САР с запаздыванием.

Критерий устойчивости Найквиста дает возможность оценивать устойчивость САР по АФЧХ ее разомкнутой части. При этом различают три случая применения критерия Найквиста.

1.Разомкнутая часть САР устойчива. Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой части системы (годограф Найквиста) при изменении частоты w от 0 до +¥ не охватывала точку с координатами [-1, j 0]. На рис. 4.6 приведены основные возможные ситуации:

1. - замкнутая система абсолютно устойчива;

2. - САР условно устойчива, т.е. устойчива только в некотором диапазоне изменения коэффициента передачи k ;

3. - САР находится на границе устойчивости;

4. - САР неустойчива.

Рис. 4.6. Годографы Найквиста, когда разомкнутая часть САР устойчива

2. Разомкнутая часть САР находится на границе устойчивости. В этом случае, характеристическое уравнение имеет нулевые или чисто мнимые корни, а у остальных корней вещественные части отрицательны.

Для устойчивости замкнутой системы , если разомкнутая часть системы находится на границе устойчивости необходимо и достаточно, чтобы АФЧХ разомкнутой части системы при изменении w от 0 до +¥, дополненная на участке разрыва дугой бесконечно большого радиуса не охватывала точку с координатами [-1, j 0]. При наличии ν нулевых корней АФЧХ разомкнутой части системы при w =0 дугой бесконечно большого радиуса перемещается от положительной вещественной полуоси на угол градусов по часовой стрелке, как показано на рис. 4.7.

Рис. 4.7. Годографы Найквиста при наличии нулевых корней

Если имеется пара чисто мнимых корней w i = , то АФЧХ при частоте w i дугой бесконечно большого радиуса перемещается на угол 180° по часовой стрелке, что отражено на рис. 4.8.

Рис. 4.8. Годограф Найквиста при наличии пары чисто мнимых корней

3. Разомкнутая часть системы неустойчива , т.е. характеристическое уравнение имеет l корней с положительной вещественной частью. В этом случае, для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты w от 0 до +¥ АФЧХ разомкнутой части САР охватывала точку

[-1, j 0) l /2 раз в положительном направлении (против часовой стрелки).

При сложной форме годографа Найквиста удобнее применять другую формулировку критерия Найквиста, предложенную Я.З. Цыпкиным, используя правила переходов. Переход АФЧХ разомкнутой части системы при увеличении w отрезок вещественной оси от -1 до -¥ сверху вниз считается положительным (рис. 4.9), а снизу вверх отрицательным. Если АФЧХ начинается на данном отрезке при w =0 или заканчивается при w =¥ , то считается, что АФЧХ совершает пол перехода.

Рис. 4.9. Переходы годографа Найквиста через отрезок P(w ) от -¥ до -1

Замкнутая система устойчива , если разность между числом положительных и отрицательных переходов годографа Найквиста через отрезок вещественной оси от -1 до -¥ равно l/2, где l – число корней характеристического уравнения с положительной вещественной частью.

Условие задания.

Пользуясь критерием устойчивости Михайлова, Найквиста определить устойчивость одноконтурной системы управления, имеющую в разомкнутом состоянии передаточную функцию вида

в формулу проставить значения К, а, b и с по варианту.

W(s) =, (1)

Построить годографы Михайлова и Найквиста. Определить частоту среза системы.

Определить критическое значение коэффициента усиления системы.

Решение.

Задачи анализа и синтеза систем управления решаются с помощью такого мощного математического аппарата, каким является операционное исчисление (преобразование) Лапласа. Задачи анализа и синтеза систем управления решаются с помощью такого мощного математического аппарата, каким является операционное исчисление (преобразование) Лапласа. Общее решение операторного уравнения представляет собой сумму слагаемых, определяемых значениями корней характеристического полинома (многочлена):

D (s) = d s n d n ) .

Построение годографа Михайлова.

А) Выписываем характеристический многочлен для замкнутой системы, описываемой уравнением (1)

D (s) = 50 + (25s+1)(0,1s+1)(0,01s+1) = 50+(625+50s+1)(0,001+0,11s+1) =0,625+68,85+630,501+50,11s+51.

Корни многочлена D (s) могут быть: нулевыми; вещественными (отрицательными, положительными); мнимыми (всегда парными, сопряженными) и комплексными сопряженными.

Б) Преобразуем к виду s→ ωj

D ()=0,625+68,85+630,501+50,11+51=0,625ω-68,85jω- 630,501ω+50,11jω+51

ω – частота сигнала, j = (1) 1/2 – мнимая единица. J 4 =(-1) 4/2 =1, J 3 =(-1) 3/2 =-(1) 1/2 = - j, J 2 =(-1) 2/2 =-1, J =(-1) 1/2 = j,

В) Выделим действительную и мнимую часть.

D = U()+jV(), где U() – действительная часть, а V() – мнимая часть.

U(ω) =0,625ω-630,501ω+51

V(ω) =ω(50,11-68,85ω)

Г) Построим годограф Михайлова.

Построим годограф Михайлова вблизи и сдали от нуля, для этого построем D(jw) при изменении w от 0 до +∞. Найдем точки пересечения U (w) и V (w) с осями. Решим задачу с использованием MicrosoftExcel.

Задаем значения w в диапазоне от 0 до 0,0001 до 0,1, рассчитаем в табл. Excel значения U (ω) и V (ω), D(ω); находим точки пересечения U (w) и V (w) с осями,

Задаем значения w в диапазоне от 0,1 до 20, рассчитаем в табл. Excel значения U (w) и V (w), D; находим точки пересечения U (w) и V (w) с осями.

Таблица 2.1 – Определение действительной и мнимой частей и самого многочлена D ()с использованием MicrosoftExcel

Рис. А, Б, ….. Зависимости U (ω) и V (ω), D(ω) от ω

По рис. А, Б, …..находим точки пересечения U (w) и V (w) с осями:

при ω = 0 U (ω)= …. и V (ω)= ……

Рис.1. Годограф Михайлова при ω = 0:000,1:0,1.

Рис.2. Годограф Михайлова при ω = 0,1:20

Д) Выводы об устойчивости системы по годографу.

Устойчивость (как понятие) любой динамической системы определяется ее поведением после снятия внешнего воздействия, т.е. ее свободным движением под влиянием начальных условий. Система является устойчивой, если она возвращается в исходное состояние равновесия после прекращения действия на систему сигнала (возмущения), выведшего ее из этого состояния. Неустойчивая система не возвращается в исходное состояние, а непрерывно со временем удаляется от него. Для оценки устойчивости системы необходимо исследовать свободную составляющую решения уравнения динамики, т.е решения уравнения:.

D (s) = d s n d n )= 0.

Проверить устойчивость системы с помощью критерия Михайлова:

Критерий Михайлова: Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.1 и рис.2), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ∞ n квадрантов, где n - степень характеристического полинома.

Из решения видно (см. рис.1 и рис.2), что годограф удовлетворяет следующим условиям критерия: Начинается на положительной вещественной полуоси при w = 0. Годограф не удовлетворяет следующим условиям критерия: не обходит в положительном направлении все 4 квадранта (степень полинома n=4) при ω.

Делаем вывод, что данная разомкнутая система не устойчива.

Построение годографа Найквиста.

А) Произведем замену в формуле (1) s→ ωj

W(s) = =,

Б) Раскроем скобки и выделим действительную и мнимую часть в знаменателе

В) Умножим на сопряженное и выделим действительную и мнимую часть

где U() – действительная часть, а V() – мнимая часть.

Г) Построим годограф Найквиста: - зависимость W() от .

Рис.3. Годограф Найквиста.

Д) Проверим устойчивость системы с помощью критерия Найквиста:

Критерий Найквиста: Для того чтобы система, которая в разомкнутом состоянии была устойчива, была устойчива и в замкнутом, необходимо, чтобы годограф Найквиста при изменении частоты от нуля до бесконечности не охватывал точку с координатами (-1; j0).

Из решения видно (см. рис.3), что годограф удовлетворяет всем условиям критерия:

Годограф меняет свое направление по часовой стрелке

Годографом не охватывается точка (-1; j0)

Делаем вывод, что данная разомкнутая система устойчива.

Определение критического значения коэффициента усиления системы.

А) В пункте 2 уже были выделены действительная и мнимая части

Б) Для того, чтобы найти критическое значение коэффициента усиления системы необходимо приравнять мнимую часть к нулю, а действительную к -1

В) Найдем из второго (2) уравнения

Числитель должен быть равен 0.

Принимаем, что , тогда

В) Подставляем в первое (1) уравнение и находим

Критическое значение коэффициента усиления системы.

Литература:

1.Методы классической и современной теории автоматического управления. Том 1.

Анализ и статистическая динамика систем автоматического управления. М: Изд. МГТУ им Баумана. 2000 г.

2. Воронов А.А. Теория автоматического управления. Т. 1-3, М., Наука, 1992

Важная теорема из теории функций комплексного переменного устанавливает: пусть функция однозначна внутри односвязного контура С и, кроме того, однозначна и аналитична на этом контуре. Если не равна нулю на С и если внутри контура С может быть лишь конечное число особых точек (полюсов), то

где -число нулей, а - число полюсов внутри С, каждый из которых учтен соответственно его кратности.

Эта теорема непосредственно вытекает из теоремы Коши о вычетах, которая устанавливает, что

Заменим на и заметим, что особенности сохраняются как в нулях, так и в полюсах Тогда вычеты, найденные в этих особых точках, будут равны кратностям особых точек с положительным знаком в нулях и отрицательным знаком в полюсах Сформулированная выше теорема теперь очевидна.

Соотношение (11.2-1) можно также записать в виде

Так как на контуре С будет в общем иметь как действительную, так и мнимую части, то ее логарифм запишется в виде

При условии, что на границе С нигде не обращается в нуль, интегрирование в (II.2-3) дает непосредственно

где обозначают произвольное начало и конец замкнутою контура С. Следовательно,

Комбинируя результаты (II.2-1) и (II.2-7), находим, что произведение на полное изменение угла (полное обращение вокруг начала координат) когда обегает контур С, равно разности между нулями и полюсами внутри контура С.

Если - полное число оборотов вокруг начала при обегающем С, то можно написать

причем контур С обходится в направлении, соответствующем возрастанию положительного угла, и оборот называется положительным, если он происходит также в направлении, соответствующем возрастанию положительного угла.

Рис. II.2-1. Замкнутый контур, охватывающий конечную часть правой полуплоскости.

Теперь эти результаты можно приложить непосредственно к задаче об определении устойчивости. Мы желаем знать, имеет ли знаменатель передаточной функции нули в правой полуплоскости.

Следовательно, контур С выбран так, чтобы полностью охватывать правую полуплоскость. Этот контур показан на рис. где большая полуокружность, охватывающая правую полуплоскость, задана соотношениями

при стремящемся в пределе к бесконечности.

Предположим, что записывается как

где целая функция от и что не имеют общих множителей. Построим далее диаграмму в комплексной плоскости, изменяя значения вдоль контура С. Эта диаграмма даст нам некоторый замкнутый контур. В общем случае будет целой функцией полиномиального вида, которая, очевидно, не имеет полюсов в конечной части плоскости. Если трансцендентна, то число Р полюсов в конечной части правой полуплоскости подлежит определению. Зная Р и определяя по диаграмме когда пробегает С, мы можем теперь определить, согласно уравнению (II.2-8), число нулей в правой полуплоскости

Рис. II.2-2. Простая одноконтурная система регулирования.

Чтобы система была устойчивой, должно быть равно нулю. Следовательно, применение этого критерия включает два этапа: первый --определение полюсов в правой полуплоскости, и второй - построение диаграммы когда пробегает С. Первый этап выполняется обычно весьма просто. Второй - может представлять значительные трудности, особенно если третьего или более высокого порядка и если содержит трансцендентные члены.

Для системы регулирования с обратной связью, показанной в общем виде на рис. сложность составления диаграммы можно заметно уменьшить, если использовать передаточную функцию разомкнутой системы. Передаточная функция замкнутой системы связана с передаточной функцией разомкнутой системы соотношением

где могут иметь как полюсы, так и нули. В задаче об устойчивости желательно знать, имеет ли полюсы в правой полуплоскости. Это эквивалентно нахождению в правой полуплоскости нулей функции или нахождению в правой полуплоскости, сдвинутой на -1, нулей функции Чтобы пояснить эффект, происходящий за счет изменения коэффициента усиления разомкнутой системы, и в то же время свести к минимуму работу по построению диаграммы Найквиста, перепишем знаменатель выражения (II.2-12) в виде где К - коэффициент усиления разомкнутой системы. Теперь полюсы идентичны нулям относительно

Чтобы применить критерий Найквиста, вычертим сначала при пробегающем контур С, который охватывает

всю правую полуплоскость. После этого подсчитаем полное число оборотов при том же перемещении вокруг точки Изменение коэффициента усиления К меняет только положение точки и не оказывает воздействия на расположение [-Число полюсов Р функции в ППП определяется непосредственно по самой функции, если она имеет вид произведения простых сомножителей, или путем более трудного расчета, если она имеет полиномиальную или трансцендентную форму. Устойчивость системы определяется тогда непосредственным применением уравнения (II.2-8), которое устанавливает

Следовательно, система устойчива только в том случае, если равно нулю, где теперь число нулей знаменателя (II.2-12) в

Рис. II.2-3. Две возможные модификации контуров с обходом полюсов на мнимой оси.

При применении критерия в этой форме следует обратить внимание на выбор контура С, охватывающего правую полуплоскость. Соотношение (11.2-1), а следовательно, и (11.2-13) требуют отсутствия особенностей отображаемой функции на контуре С. Часты случаи, когда имеет полюс в начале координат или даже несколько пар комплексно сопряженных полюсов на мнимой оси. Чтобы рассмотреть эти специальные случаи, конгур С модифицируется при помощи обходов каждой из особенностей по очень малым полуокружностям, как показано на рис. II.2-3. Если особенности являются полюсами, то модифицированный контур С может проходить либо справа, либо слева от них, как показано на рис. II.2-3,а и II.2-3,б соответственно. Если особенность не является полюсом, то контур должен проходить всегда справа от нее, так как соотношение (II.2-1) допускает внутри контура С только такие особенности, как полюсы. Те полюсы на мнимой оси, которые обходятся слева, лежат при этом внутри контура С и, следовательно, должны быть учтены в Р. В этом случае контур С в ближайшей окрестности особой точки выбирается обычно в виде

где угол изменяется от до в пределе стремится к нулю.

Годограф при пробегающем контур С, состоит в основном из четырех частей. Годограф при

исключая окрестности особенностей на мнимой оси, является просто частотной характеристикой разомкнутой системы. Следовательно, годограф при может быть получен путем отображения его при относительно действительной оси. Когда пробегает бесконечную полуокружность, значение для всех физически осуществимых систем равно нулю или, самое большее, конечной постоянной величине. Наконец, годограф при пробегающем малые полуокружности в окрестности полюсов на мнимой оси, определяется непосредственной подстановкой в эту функцию выражения (II.2-14). Таким образом, отображение контура С на плоскость функции завершено.

При применении критерия в этой форме характер ограничений, наложенных на становится очевидным. Во-первых, может иметь в правой полуплоскости лишь конечное число особенностей типа полюс. Во-вторых, может иметь лишь конечное число особенностей (полюсов или точек ветвления) на мнимой оси. Класс функций можно расширить, чтобы включить функции, имеющие точки ветвления, если только точки ветвления лежат в левой полуплоскости и если используется главное значение функции. В-третьих, существенные особенности вида в числителе допустимы, поскольку абсолютное значение этой функции, когда изменяется в пределах правой полуплоскости, заключено между и 0.

Применение критерия Найквиста целесообразно показать на примере. Пусть регулируемая система с обратной связью определена соотношениями

Передаточная функция заданных элементов соответствует двухфазному индукционному мотору, работающему на частоте , от однополупериодного магнитного усилителя. Наличие отрицательного затухания связано с низким сопротивлением ротора. Возникает первый вопрос: можно ли заданные элементы стабилизировать только за счет коэффициента усиления? Положим, следовательно,

Передаточная функция разомкнутой системы принимает вид

Мы видим, во-первых, что имеет только один полюс в правой полуплоскости и этот полюс находится в точке Примерная диаграмма при пробегающем контур С, изображенный на рис. II.2-4, а, приведена на рис. II.2-4, б и показывает, что при выбранном коэффициенте усиления вокруг точки существует один положительный оборот.

Рис. II.2-4. Примеры диаграмм Найквиста.

Следовательно, с помощью критерия Найквиста, выраженного уравнением (II.2-13), приходим к результату

Увеличение К создает возможность большего числа положительных оборотов вследствие спиральной природы части диаграммы, обусловленной множителем мы можем, следовательно, заключить, что система неустойчива при всех положительных значениях К.

При отрицательных значениях К мы можем либо повернуть нашу диаграмму относительно начала и рассмотреть обороты вокруг точки либо использовать существующую диаграмму и рассмотреть обороты вокруг точки Последний способ проще; он непосредственно показывает, что, как минимум, положительные обороты вокруг отсутствуют. Это дает по крайней мере один нуль в правой полуплоскости при отрицательных значениях К. Поэтому мы приходим к выводу, что система неустойчива при всех значениях К, как положительных, так и отрицательных, и следовательно, чтобы сделать систему устойчивой, требуется некоторая коррекция.

Критерий Найквиста можно применять также тогда, когда частотная характеристика разомкнутой системы построена по экспериментальным данным. Передаточная функция разомкнутой системы должна быть в таком случае устойчивой и, следовательно, не может иметь полюсов в правой полуплоскости, т. е. . Чтобы правильно построить годограф Найквиста, следует позаботиться о точном определении поведения системы при очень низких частотах.

При применении критерия Найквиста к многоконтурным системам построение начинается с самой внутренней петли и продолжается к внешним петлям при тщательном подсчете числа полюсов в ППП от каждой отдельной петли. Труд, вкладываемый в этот метод, часто можно сократить, уничтожая некоторые контуры в результате преобразования блок-схемы. Выбор последовательности построения годографа для многоконтурных систем зависит от структурной схемы, а также от расположения заданных и корректирующих элементов в контурах.

Построение годографов Найквиста по передаточной функции разомкнутой системы заданной в виде полинома

Частотный критерий Найквиста при исследовании устойчивости автоматических систем базируется на амплитудно-фазовой частотной характеристики разомкнутой системы и может быть сформулирован следующим образом:

если характеристическое уравнение разомкнутой системы n -го порядка имеет k корней с положительной вещественной частью (k = 0, 1, ….. n) и n-k корней с отрицательной вещественной частью, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф амплитудно-фазовой частотной характеристики разомкнутой системы (годограф Найквиста) охватывал точку (-1, j0) комплексной плоскости на угол k р, или что тоже самое, охватывал точку (-1, j0) в положительном направлении, т.е. против часовой стрелки, k раз.

Для частного случая, когда характеристическое уравнение разомкнутой системы не имеет корней с положительной вещественной частью (k = 0), т.е. , когда она устойчива в разомкнутом состоянии, критерий Найквиста формулируется следующим образом:

система автоматического регулирования устойчива в замкнутом состоянии, если амплитудно-фазовая частотная характеристика разомкнутой системы при изменении частоты от 0 до? не охватывает точку комплексной плоскости с координатами (-1, j0).

Критерий устойчивости Найквиста удобно применять для систем с обратной связью, особенно систем высокого порядка.

Для построения годографа Найквиста воспользуемся передаточной функцией разомкнутой системы в символьном виде из Практического занятия №5

Запишем ее в символьно-цифровом виде для заданных параметров всех элементов системы, кроме коэффициента передачи магнитного усилителя:

Запишем уравнение амплитудно-фазовой частотной характеристики, выделим вещественную и мнимые частотные характеристики и построим семейство годографов Найквиста в функции частоты и коэффициента передачи магнитного усилителя.

Построения графика амплитудно-фазовой частотной характеристики в MathСad

Рис.3. Семейство кривых годографа Найквиста, построенный для передаточной функции разомкнутой системы в функции от k му .

Из рис.3 видно, что один из годографов Найквиста проходит через точку с координатами (j0, -1) . Следовательно, в заданной области изменения коэффициента передачи магнитного усилителя есть и его критическое значение. Для его определения воспользуемся следующими соотношениями:

Следовательно, критический коэффициент передачи магнитного усилителя есть:

k мукр =11.186981170416560078

Убедимся, что это действительно так. Для этого построим кривые годографа Найквиста для трех значений коэффициента передачи магнитного усилителя: k му = 0.6 k мукр ; k му = k мукр ; k му =1.2 k мукр

Рис.4.

k му = 0.6 k мукр; k му = k мукр; k му =1.2 k мукр

Кривые рис.4 подтверждают, что критический коэффициент передачи магнитного усилителя найден верно.

Использование л.а.ч.х. и фазовых частотных характеристик для анализа устойчивости системы

Критерий устойчивости системы по логарифмической амплитудной частотной характеристике (л.а.ч..х) и фазовой частотной характеристике можно сформулировать следующим образом:

Система автоматического регулирования, неустойчивая в разомкнутом состоянии, устойчива в замкнутом состоянии, если разность между числами положительных переходов (переход фазовой частотной характеристики снизу вверх через линию ц(щ) = -180 ° ) и числами отрицательных переходов (переход фазовой частотной характеристики сверху в низ через линию ц(щ) = -180 ° ) фазовой частотной характеристики ц(щ) через линию ц(щ) = -180 ° равно нулю в диапазоне частот, на которых л.а.ч..х (L(щ)> 0) .

Для построения фазовой частотной характеристики, желательно представить передаточную функцию в виде типовых динамических звеньев.

и строить фазовую характеристику, используя выражение:

«+» - соответствует типовым динамическим звеньям числителя передаточной функции;

«-« - соответствует типовым динамическим звеньям знаменателя передаточной функции.

Для построения асимптотической л.а.ч.х. используем передаточную функцию разомкнутой системы, представленной в виде типовых динамических звеньев:

Для этого используем передаточную функцию вида:

Представим эту передаточную функцию в виде типовых динамических звеньев:

Параметры типовых динамических звеньев определяются, как показано ниже:

Уравнение фазовой характеристики будет иметь вид:

Определим частоту, при которой фазовая частотная характеристика пересекает ось ц(щ) = -180 °

Для построения л.а.ч.х. воспользуемся выражением:

На рис.5 представлены графики л.а.ч.х для двух значений коэффициента передачи магнитного усилителя k му = 10 и k му = 80 .

Рис.5.

Анализ л.а.ч.х. и фазовой частотной характеристики показывают, что при увеличении коэффициента передачи магнитного усилителя от 8 до 80 система из устойчивой становится неустойчивой. Определим критический коэффициент передачи магнитного усилителя.

Если нет дополнительных требований по запасам устойчивости к системе, то рекомендуется принимать их равными:

ДL(щ) = -12db Дц(щ) = 35°ч 45

Определим, при каком коэффициенте передачи магнитного усилителя это условие выполняется.

Это же подтверждается графиками, приведёнными на рисунке 6.