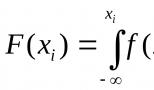Элективный курс по математике "абсолютная величина". Образовательный портал Раздел III. Учебно-тематический план

Уравнения и их системы, содержащие знак абсолютной величины
(методическая разработка)

Параграф 1. Основные сведения.

Пункт 1. Определение абсолютной величины числа. Решение простейших уравнений.

Знакомство с понятием абсолютной величины числа (модуля числа) лучше начинать с его геометрической интерпретации: в геометрии модуль - это расстояние от точки, изображающей данное число на числовой оси или координатной плоскости, до начала координат. Так, число 5 расположено на числовой оси справа от нуля, а число -5 слева от нуля, но расстояния от точек, изображающих эти числа, до начала координат одинаковы и равны 5. Значение абсолютной величины числа a обозначается скобками: .
Поясним геометрическое определение модуля графически:

Соответственно устанавливается алгебраическое определение модуля некоторой величины:

.
Рассмотрим теперь простейшие (но важные для понимания материала) уравнения, включающие знак абсолютной величины. Под будем понимать некоторое алгебраическое выражение, содержащее неизвестную переменную.

А.Уравнения вида, где a - заданное число. (1)
Уточним стоящую перед нами задачу: если x - некоторое решение уравнения (1), то, согласно геометрическому определению модуля, точка f на числовой прямой расположена на расстоянии a от начала координат. Поэтому, если a0, то имеем две искомые точки: f1=-a, f2=a.

Итак, уравнение (1): при a0 имеет своими решениями решения уравнений и.
Коротко последнее утверждение записывается так:

Читается: множество решений уравнения при a>0 есть объединение множеств решений уравнений и.

Пример 1. Решить уравнения: а) ; б) ; в) ; г) .

Решения:
а) 
Ответ: x1=1 ; x2=6.

Б) => решений нет, т.к. модуль (абсолютное значение) любой величины не может быть отрицателен.
Ответ: решений нет.

В) 
Ответ: x1=-3; x2=0.

Г) 
Ответ: x1=-3; x2=3.

Пример 2. Решить уравнения: а) ; б) .

Решения:
а) согласно (1) в данном случае = , т.е. f(x)≥2. Поэтому уравнение не имеет решений.
Ответ: решений нет.

Ответ: x1=-5; x2=0; x3=2; x4=7.

В. Уравнения вида (2) и (3).
Поскольку модуль любого выражения - величина неотрицательная, следовательно, если x - решение уравнения (2), то и правая часть данного уравнения неотрицательна, т.е. . Но тогда в левой части этого же уравнения по определению равен просто. Вывод: при обязательном условии мы пришли к тождеству, поэтому решения неравенства будут одновременно решениями уравнения (2).
Рассуждая аналогично, получаем, что все решения неравенства являются решениями уравнения (3).

Пример 3. Решить уравнения: а) ; б) ; в) .
Решения:
а) 
Ответ: .

Б) 
Ответ: .

С. Уравнения вида (4).
Если x - решение уравнения (4), то, согласно геометрическому определению модуля, расстояния на числовой прямой от точек f и g до начала координат равны, т.е. либо точки f и g совпадают (имеем:), либо симметричны друг другу относительно начала координат (имеем:). Поэтому

В качестве особого следует упомянуть уравнение.
Решениями данного уравнения являются все x, при которых выражение определено.

Пример 4. Решить уравнения: а) ; б) ; в) ; г) .

Решения:

А) Данное уравнение есть уравнение вида, где. Эта функция определена при любых действительных x, поэтому x - любое.
Ответ: x - любое.

Б) 
Ответ: .

В) 
.
Ответ: .

Замечание: т.к.  , то обе части уравнения (4) можно возвести в квадрат, освобождаясь от модулей, причем среди корней получившегося уравнения не окажется «лишних» для нас.
Например: , откуда получаем.

D. Уравнения вида. (5)
Имеем: сумма неотрицательных по определению выражений равна нулю. Следовательно, каждое из слагаемых должно равняться нулю. Т.к. тогда и только тогда, когда, и тогда и только тогда, когда, следовательно уравнение (5) равносильно системе: .
Решать данную систему рациональнее следующим образом: выбрав из уравнений более простое, найти его решения и проверить их на соответствие всей системе подстановкой в оставшееся уравнение.

Пример 5. Решить уравнения: а) ;
б) .

Решения:

А)
Подставляем поочередно x=-1 и x=1 в первое уравнение, получаем, что оба уравнения системы выполнены только при x=-1.
Ответ: x=-1.

Б) Данное уравнение эквивалентно (равносильно) системе:

Ответ: x=-2.
Пункт 2. Метод интервалов. Решение простейших систем.

Пусть требуется решить уравнение. Согласно алгебраическому определению модуля:

Таким образом точка x=2 разбивает числовую ось на два интервала, на каждом из которых модульные скобки над выражением x-2 раскрываются по разному:

Поэтому решение исходного уравнения сводится к последовательному рассмотрению двух возможных ситуаций:
а) Предположим, что x - решение исходного уравнения, причем.
Тогда и имеем: , что соответствует условию а). Поэтому является решением исходного уравнения.
б) Предположим, что x - решение исходного уравнения, причем
Тогда и имеем: , что не соответствует условию б). Поэтому не является решением исходного уравнения.
Рассмотренное уравнение имеет единственный корень: .

Особенно метод интервалов полезен, если в уравнении несколько модульных скобок. Единственное затруднение - в определении четкой последовательности действий, поэтому настоятельно рекомендуется придерживаться следующего плана:

1) Определить все значения неизвестного, при которых выражения под знаками модуля обращаются в ноль или становятся неопределенны, и отметить полученные точки на числовой оси.
2) Решить исходное уравнение на каждом из выявленных числовых промежутков.
3) Объединить найденные решения в общий ответ.

Полезно по окончании первого этапа выписать, как именно в зависимости от положения неизвестного на числовой оси раскрываются каждые модульные скобки.

Упражнение: раскрыть модульные скобки в выражении.
Сначала рассматриваем внутренние скобки: при, поэтому отмечаем на числовой оси точку.
Затем рассматриваем внешние скобки: решаем уравнение (решение проводится изложенным выше методом интервалов:

Первое уравнение не имеет корней, а корнями второго являются числа 1 и -1, но x=1 не удовлетворяет условию).
Далее, выбрав произвольное x, большее -1, например x=0, убеждаемся, что при x>-1 ; выбрав произвольное x, меньшее -1, например x=-2, убеждаемся, что при x

В итоге на числовой оси отмечены точки x=-1 и x=0. На каждом из получившихся промежутков модули в исходном выражении раскрываются по «цепочке» (*):

При;
при;
при.

Пример 6.Решить уравнения: а) ; б) ; в) ; г) .
Решения:

А) I этап.
. Поэтому:
.

II этап.
1) Тогда поэтому исходное уравнение примет вид: .

2) . Тогда поэтому исходное уравнение примет вид: что не соответствует рассматриваемому отрезку, поэтому на данном промежутке исходное уравнение корней не имеет.
3) Тогда поэтому исходное уравнение примет вид: что соответствует рассматриваемому полуинтервалу, поэтому исходного уравнения.
III этап.
На первом и втором числовых промежутках уравнение решений не имеет. На третьем получили решение.
Ответ: .

Б) I этап.
Поэтому:

Имеем следующие числовые промежутки:

II этап.
1) Тогда поэтому исходное уравнение примет вид:
Получили верное числовое равенство, поэтому любое из данного полуинтервала является решением исходного уравнения!
2) . Имеем, раскрывая модули согласно результатам первого этапа: что соответствует рассматриваемому отрезку, поэтому есть решение исходного уравнения.
3) Раскрываем модули:
Получили неверное числовое равенство, поэтому на данном полуинтервале исходное уравнение корней не имеет.

III этап.
На первом промежутке:
На втором промежутке:
На третьем промежутке: нет решений.
Итог:
Ответ:

В) I этап.
Сначала рассматриваем «внутренний» модуль, затем «внешний»:
1) x=0 при x=0 =>
2)
Данное уравнение следует решить отдельно. Заметим при этом, что числовые промежутки, которые следует рассматривать, уже известны (см. (*)):
при имеем нет решений
при имеем,
но x1 не соответствует условию.
Итак, .
Само же выражение положительно при (например, x=10:) и отрицательно при (например, x=1:). Поэтому:

Имеем следующие числовые промежутки:

II этап.
На каждом промежутке сначала раскрываем внешние модульные скобки, затем внутренние.
1) .
: , что соответствует рассматриваемому интервалу, поэтому есть решение исходного уравнения.
2) .
: .
Проверим соответствие найденных корней заданному отрезку: - очевидно, проверим теперь, выполняется ли соотношение

Очевидно, т.е. является посторонним корнем.
3) .
: . Проверим полученное на соответствие заданному полуинтервалу: является корнем исходного уравнения.

III этап.
;
;
.
Ответ: .

Г) Особенностью данного уравнения является присутствие неизвестной величины в знаменателе дроби, поэтому необходимо на каждом числовом промежутке находить область определения уравнения (ООУ).

Имеем два полуинтервала:

II этап.
1) раскрывая модуль и упрощая, получаем уравнение.
ООУ: . При из ООУ, очевидно, получаем верное равенство, т.о. решениями исходного уравнения являются все.
2) раскрывая модуль и упрощая, получаем уравнение ООУ: . Тогда, что соответствует рассматриваемому полуинтервалу, поэтому есть решение исходного уравнения.

Ответ: .

B. Решение несложных систем уравнений, содержащих знак абсолютной величины, не должно вызывать трудностей: как правило, достаточно использовать известный учащимся метод подстановки.

Пример 7. Решить системы уравнений:
а) б) в) г)

Решения:
а) Из первого уравнения системы получаем:
Тогда, после подстановки (*), второе уравнение примет вид:
.
Согласно (*): при при.
Ответ:

Б) Из первого уравнения системы получаем:
.
При из второго уравнения системы получаем
соответственно, x=2.
При из второго уравнения системы получаем y=-5.
Ответ: .

В) Из второго уравнения системы получаем:
.
При из первого уравнения получаем.
При из первого уравнения получаем; соответственно, .
Ответ: .

Г) В данном случае проще воспользоваться методом сложения, а для решения получающегося уравнения - методом интервалов.
.

1) получаем решений нет;
2) получаем.
Вывод: и теперь из первого уравнения получаем.
Ответ: .

Пункт 3. Рациональные методы решения: простейшие геометрические и алгебраические соображения, обобщение метода интервалов, замена переменной.

А. Некоторые простые уравнения допускают ясную геометрическую интерпретацию, решение их значительно упрощается - «неподходящие» числовые промежутки сразу исключаются из рассмотрения.
Покажем сначала, что геометрически есть расстояние между точками числовой оси, изображающими числа и. Для этого на числовой оси, где уже отмечены и перенесем начало координат в точку. Координаты точек изменятся:

Расстояние между точками и это, согласно новой системе отсчета, расстояние между точками и, т.е.

Пример 8. Решить уравнения: а) б) в) г) д) .

Решения:
а)Требуется указать на числовой оси такие x, что сумма расстояний от x до 1 и от x до 3 равна 3 ед. Расстояние между 1 и 3 равно 2 ед., поэтому (иначе). Получается, что x лежит либо левее 1, либо правее 3 - на некотором расстоянии от них, причем в любом случае. Поэтому, откуда.

Теперь легко находятся два значения x.
Ответ: .
б) Требуется указать на числовой оси такие точки 2x, что расстояние от 2x до -2 больше расстояния от 2x до 7 на 9,12 ед.
Если, рассматриваемая разность всегда равна -9;
Если, рассматриваемая разность всегда равна 9;
Если, рассматриваемая разность меньше либо равна 9.
Пусть, например, :

Тогда.
Ответ: решений нет.

В) Перепишем уравнение в виде. Поэтому искомое x лежит в три раза ближе к 3, чем к 2:

=> нет решений, так как x всегда ближе к 2, чем к 3;
«на глазок», ;
=> «на глазок», .
Ответ: .

Г) Данный пример показывает, что очень полезным бывает «строгое» разбиение числовой оси на промежутки (без «перекрытий» вида):

Нет решений;
(соответствует рассматриваемому полуинтервалу);
нет решений.
Ответ: .

Д) Начнем с применения метода интервалов:

Замечем теперь, что при и за пределами данного отрезка. Имеет смысл поэтому рассматривать уравнение только на этом отрезке, причем получаем: . Очевидно, x=2.
Ответ: .

B. Изучая области значений правой и левой частей уравнения, нередко удается упростить ход решения, исключая заведомо неподходящие значения неизвестного.

Пример 9. Решить уравнения: а) б) в) г) .

Решения:

А) Левая часть уравнения неотрицательна при любых x, а в правой части - отрицательное число.
Ответ: решений нет.

Б) Левая часть уравнения неотрицательна при любых x, поэтому, если x - решение, то правая часть также неотрицательна. Значит, достаточно рассмотреть только значения x из области то есть. Но тогда Получили неверное равенство.
Ответ: решений нет.
в) Выражение положительно при любых x, поэтому внешние модульные скобки можно снять. Кроме того, если x - решение, то правая часть также положительна, поэтому достаточно рассмотреть x из области. Тогда и получаем (соответствует области).
Ответ: .

Г) Сумма двух неотрицательных слагаемых равна 1, если каждое из слагаемых не превосходит единицы: Так как, то на указанном отрезке получаем Если, то, очевидно, что нас не устраивает. Поэтому, если x - решение, то. А на этом полуинтервале получаем
Ясно, что - посторонний корень.
Ответ: .

C. Рассмотрим уравнения вида (1)
Решая данное уравнение методом интервалов, мы получим уравнение для тех промежутков, где и уравнение для промежутков, где. Ясно, что нет смысла рассматривать каждый промежуток по отдельности, - достаточно разделить их на две указанные группы: для каждой надо решить соответствующее уравнение и проверить полученные корни на соответствие поставленному условию. Таким образом

Возможен и другой вариант: ясно, что среди решений уравнения истинными корнями уравнения (1) будут те, при которых Проводя аналогичные рассуждения для случая, получаем

Какой из вариантов избрать, зависит от вида функций, например, если решения уравнений проще подставлять для проверки в, то разумнее применить первый способ.

Пример 10. Решить уравнения: а)
б) в) .

Решения:

А) Предположим,
Тогда имеем
Предположим,
Тогда имеем нет решений.
Проверим теперь полученные корни. Перепишем исходное уравнение:
. Поскольку, оба корня истинны.
Ответ:

Б) Предположим,
Тогда имеем нет решений.
Предположим,
Тогда имеем
Для определения истинности этих корней проверим выполнение условия Получаем: Очевидно, корень посторонний. Для проверки выясним, верно ли, что. Так как то есть рассматриваемое неравенство не выполнено.
Ответ: решений нет.

В) Перепишем уравнение: Используем следующую графическую иллюстрацию: (здесь представлены графики функций и).

Теперь ясно, что получившиеся числовые промежутки следует объединить в три следующие группы:
1) . Получаем (соответствует поставленному условию).
2) Получаем
нет решений.
3) Получаем
нет решений.
Ответ: .

D. Метод замены некоторого выражения новой буквенной переменной хорошо известен. Можно заметить только, что при решении уравнений, содержащих модуль, часто удается сразу ограничить область изменения новой переменной.
Пример 11. Решить уравнения или систему уравнений: а) ;
б) ;
в)

Решения:
а) Заменив новой переменной получаем систему что означает, что и являются корнями уравнения Получаем.
Ответ: .

Б) Заменив выражение новой переменной получим уравнение. Получаем:
. Остается решить данные уравнения.
Ответ: .

В) Перепишем уравнение в виде:
Очевидно, возможны два варианта:
1)
2) Заменим новой переменной. Заметим, что по смыслу замены и согласно ОДЗ данного уравнения, т.е. (*) А уравнение примет вид. Так как, получаем
Учитывая (*), окончательно получаем
Значит, Заменяя на, получаем
Так как по смыслу замены, получаем

Контрольные задания к §1.
1) Решите, пользуясь определением модуля числа:
а) б) в) г) д) е) ж) з) и) к) .

2)Решите «стандартные» уравнения:
а) б) в) г) д) е) ж) з) и) .

3) Решите методом интервалов:
а) б) ; в) г) д) е) ж) з) и) к) л) м) н) о) п) р) с) т) у) ф) х) ч)

4)Решите рациональным способом:
а) б) в) г) д) е) ж) з) и) к) л) м) н)

5)Решите системы уравнений:
а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р)

Задания на построение графиков функции «модуль» и задачи с параметрами традиционно - это одна из самых трудных тем математики, поэтому она всегда включена в задания повышенного и высокого уровня ГИА и ЕГЭ.

Понятие «модуль» изучается в школе с 6 класса, причем на уровне,только определения и вычисления, несмотря на то, что он широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике будут изучаться понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.

Перед выпускниками стоит проблема – удачно сдать ГИА в 9классе, а в дальнейшем и ЕГЭ.

В этом году на уроках математики мы познакомились с понятием линейной функции и научились строить ее график. Было показано, что этот ее график берется за основу построения функции «модуль». Кроме того, учитель сказала, что уравнения бывают с одним и несколькими модулям. Я решила глубже изучить эту тему, тем более, что она мне пригодится при сдаче экзаменов.

Тема «Графический метод решения уравнений, содержащих абсолютную величину»

Цель работы : исследование возможности рационального построения графиков с модулями для решения уравнений, содержащих модуль и параметр

Изучить теорию по решению методов уравнений с модулем.

Научиться решать уравнения 1 й степени, содержащие знак абсолютной величины.

Классифицировать графические методы решения уравнений.

Проанализировать достоинства и недостатки различных методов построения графиков функции «модуль».

Узнать, что такое параметр

Применить рациональные методы для решения уравнений с параметром

Объект – методы решения уравнений с модулем

Предмет графический метод решения уравнений

Методы исследования: теоретические и практические:

теоретические - это изучение литературы по теме исследования; интернет – информации;

практические- это анализ информации, полученной при изучении литературы, результатов, полученных при решении уравнений с модулем различными способами;

сравнение способов решения уравнений предмет рациональности их использования при решении различных уравнений с модулем.

Глава I

Понятия и определения

1.1.Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике изучаются понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.

Слово «модуль» произошло от латинского слова «modulus », что в переводе означает «мера». Это слово имеет множество значений и применяется не только в математике, физике и технике, но и в архитектуре, программировании и других точных науках.Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля был введен в XIX веке Вейерштрассом.

В архитектуре модуль– исходная единица измерения, устанавливаемая для данного архитектурного сооружения.В технике – это термин, применяемый в различных областях техники, служащий для обозначения различных коэффициентов и величин, например, модуль упругости, модуль зацепления.В математике модуль имеет несколько значений, но я буду рассматривать его как абсолютную величину числа.

Определение: Модулем (абсолютной величиной) действительного числа а называется само это число, если а ≥0, или противоположное число – а , если а<0; модуль нуля равен нулю.

Модуль-это расстояние на координатной прямой от нуля до точки.

1.2. Уравнение с модулем – это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Решить уравнение-это значит найти все его корни, или доказать, что корней нет. Методы решения уравнений с модулем:

1.По определению модуля - «снятие модуля». Решение происходит на основе определения.

2.Аналитический метод- решение уравнений с использованием преобразований выражений, входящих в уравнение и свойств модуля.

3.Метод интервалов: раскрытие модуля на интервалах и полуинтервалах, образованными «нулями» модулей.

4.Графический метод. Суть этого способа заключается в том, чтобы построить графики данных функций, представляющих левую и правую часть уравнения. В случае, если графики пересекутся, то абсциссы точек пересечений данных графиков будут являться корнями данного уравнения.

1.3.Методы построения графиков функции с модулем

1.3.1. По определению. Строятся две прямые у=кх+в, где х>0, у=-кх+в, где х <0

1.3.2 Метод симметрии. Строится график у=кх+в, при х>0.Часть прямой при х <0 отображается относительно оси абцисс.

1.3.3.Преобразование функций:

а) у=|x |+n график сдвигается вверх по оси ординат на в единиц

б) у=|x |-n график сдвигается вниз по оси ординат

с) у=|x +n | график сдвигается влево по оси абцисс

d )у=|x -n | график сдвигается вправо по оси абцисс

1.3.4. Метод интервалов. Координатная прямая разбивается на интервалы и полуинтервалы нулями модулей. Далее, используя определение модуля, для каждой из найденных областей получим уравнение, которое необходимо решить на данном промежутке и получить функцию.

1.3.5. Метод расширения областей нулей. В том случае, когда модулей несколько, удобнее не раскрывать модули, а использовать следующее утверждение: алгебраическая сумма модулей n линейных выражений представляет собой кусочно-линейную функцию, график которой состоит из n +1 прямолинейных отрезков.

Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна - произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя - с абсциссой, большей большего из корней.

1.4. Имеем уравнение ax+b=c. В этом уравнении х – неизвестное, a,b,c – коэффициенты, которые могут принимать различные числовые значения. Заданные таким образом коэффициенты называются параметрами. Одно уравнение с параметрами задает множество уравнений (для всех возможных значений параметров).

это все уравнения, которые задает уравнение с параметрами ax+b=c.

Решить уравнение с параметрами – это значит:

Указать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров.

Найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение определяет корень уравнения.

1.5.Выводы:

Таким образом, существуют разные методы построения графиков с модулем, которые необходимо исследовать на возможность их рационального применения.

Глава II

Анализ методов построения графиков функций, содержащих модуль, и применение

«График – это говорящая линия,

которая может о многом рассказать»

М.Б.Балк

2.1. Изучая виды уравнений с модулем, мы увидели, что их можно и разделить по типам и методам решения.

Таблица. Классификация типов уравнений и их методов решения.

Тип уравнения

Вид уравнения

Метод решения

1.Уравнение с одним модулем

|xn|=a

|x|n=a

1.По определению модуля

2.Графический

3.Аналитический

2.Уравнение, содержащее 2 модуля

|xn||xm|=a

1.По определению модуля

2.Графический

3.Метод интервалов

4.Аналитический

3.Вложенные модули

|||xn|m||= а

1.По определению модуля

2.Графический

Вывод: таким образом, классификация уравнений дает нам общие методы решения всех типов уравнений - это по определению модуля и графический метод.

2.2.Анализ построения графиков .

2.2.1. Тип 1. Построение у=|x |

2.2.1.1.По определению .

1.Строим прямую у=х

2.Выделяем часть прямой при х0

3.Строим прямую у=-х

4.Выделяем часть прямой при х<0

2.2.1.2. Метод симметрии

1.Строим прямую у=х

2.Строим симметрию относительно оси абцисс при х<0

2.2.1.3. Построение у=|x -2|

1.Строим прямую у=х-2

2.Выделяем часть прямой при х-20

3.Строим прямую у=-х+2

4.Выделяем часть прямой при х-2<0

Вывод: метод симметрии рациональнее

2.2.2. Тип 2.

Задание: построить график у=

2.2.2.1.Метод интервалов

1. на
получаем у=-х+3+1-х-4 ; у = -2х

2. на
получаему=-х+3-1+х-4; у = -2

3. на
получаем у=х-3-1+х-4; у = 2х-8

4.Строим все прямые.

5.Выделяем части прямых на интервалах

2.2.2.2.Метод расширения областей нулей

1.Нули: 3 и 1; расширенная область: 2,4,0

2.Вычисляем значения в: 3,1,2,4,0 это: -2, -2, -2, 0, 0

3.Расставляем точки с их координатами и соединяем

Вывод: Метод расширения области нулей рациональнее

2.2.3. Тип 3. Вложенные модули-«матрешка»

Исследуем построение у=||х|-1|

2.2.3.1. По определению модуля

По определению главного модуля имеем:

1) х>0 у=|х|-1

2) х<0 у=-|х|+1

2. «Снимаем» следующий модуль:

Модуль: у=х-1, х>0 и у=-х+1 х<0

у=-х+1 х>0 у=х-1 х<0

3. Строим графики

2.2.3.2.Метод симметрии

1. у=|х|-1
у=х-1,симметрия

2. Симметрия относительно оси абцисс части графика, где х-1<0

Вывод: метод симметрии рациональнее.

2.2.4. Сведем анализ результатов в таблицу:

Знания и умения

Недостатки

По определению

Определение модуля

Знать: как определяются координаты точек прямых

Уметь выделять часть прямой по неравенству

Громоздкие решения

Применение большого объема знаний

При «снятии» модуля можно допустить ошибки

Метод симметрии

Знать и уметь применять преобразование функции

Строить симметрию относительно оси абцисс

Знание алгоритмов преобразования графиков

Метод интервалов

Находить нули модуля

Определять интервалы и полуинтервалы

Раскрывать модули

Вычислять модули

Приводить подобные слагаемые

Уметь строить точки по их координатам

Строить прямые

Громоздкие решения

Много вычислений и преобразований при снятии нулей

Занимает много времени

Правильность определения интервалов и полуинтервалов

Метод расширения области нулей

Находить нули модуля

Уметь расширять область нулей

Уметь вычислять модули в этих точках

Уметь строить точки по их координатам

Допуск ошибок в вычислениях

Метод преобразований функций

Знать алгоритм преобразования

Уметь строить точки по их координатам

Уметь вычислять координаты точек

Уметь применять алгоритм преобразования

Знание алгоритмов преобразования графиков

Вывод: анализируя таблицу, делаем вывод, что метод симметрии и расширения области нулей самые рациональные, т.к. содержат меньше всего действий для построения, а значит экономят времени.

2.3.Применение рациональных методов построения графиков к решению уравнений с модулем и параметром

2.3.1. Решить уравнение:

Строим у=
и у=0,5-х

2.Расширенная область:-1,2

3.(0;-1), (1;1), (-1;-1) (2;1)

4.Проводим отрезки и лучи

2.3.2. ЕГЭ 2009г. Найдите все значения а, при каждом из которых уравнение
, имеет ровно 1 корень.а =7. в ходе проделанной работы нам удалось изучить и проанализировать разные методы построения графиков. В результате анализа и сравнения методов построения графиков получили следующие выводы:

Перевод алгебраической задачи на язык г рафиков позволяет избежать громоздких решений;

При решении уравнений, содержащих модуль и параметр, графический способ является более наглядным и сравнительно более простым;

При построении графиков, содержащих 2 модуля и «матрешку» практичнее метод симметрии;

Хотя графический способ решения уравнений является приближенным, т.к. точность зависит от выбранного единичного отрезка, толщины карандаша, углов под которыми пересекаются линии и т.д., но этот метод позволяет оценивать кол-во корней уравнений для решения уравнений с параметром.

Учитывая, что одни из самых популярных заданий на ЕГЭ и ГИА уравнения с модулем, то, что главным моим результатом является то, что я могу решать уравнения с модулем и параметром графическим способом.

Список литературы

1.Данкова И. «Предпрофильная подготовка по математике», Москва, 2006г.

2. Внеклассная работа по математике. Альхова З.Н., Макеева А.В., г. Саратов: Лицей, 2003.

3.Математика. Учебное пособие под редакцией Муравья Л.Я., г. Москва Бридж, 1994.

4. Математика. 8-9 классы: сборник элективных курсов. Выпуск-2.Автор-составитель: М.Е. Козина., г. Волгоград: Учитель,2007

5. Ястребинецкий Г.А. Задачи с параметрами. М,2006г.

Уравнения и их системы, содержащие знак абсолютной величины
(методическая разработка)

Параграф 1. Основные сведения.

Пункт 1. Определение абсолютной величины числа. Решение простейших уравнений.

Соответственно устанавливается алгебраическое определение модуля некоторой величины:

Читается: множество решений уравнения при a>0 есть объединение множеств решений уравнений и.

Пример 1. Решить уравнения: а) ; б) ; в) ; г) .

Решения:
а) 
Ответ: x1=1 ; x2=6.

В) 
Ответ: x1=-3; x2=0.

Г) 
Ответ: x1=-3; x2=3.

Пример 2. Решить уравнения: а) ; б) .

Решения:
а) согласно (1) в данном случае = , т.е. f(x)≥2. Поэтому уравнение не имеет решений.
Ответ: решений нет.

Ответ: x1=-5; x2=0; x3=2; x4=7.

Пример 3. Решить уравнения: а) ; б) ; в) .
Решения:
а) 
Ответ: .

Б) 
Ответ: .

Пример 4. Решить уравнения: а) ; б) ; в) ; г) .

Решения:

Б) 
Ответ: .

В) 
.
Ответ: .

Пример 5. Решить уравнения: а) ;
б) .

Решения:

Б) Данное уравнение эквивалентно (равносильно) системе:

Ответ: x=-2.
Пункт 2. Метод интервалов. Решение простейших систем.

Пусть требуется решить уравнение. Согласно алгебраическому определению модуля:

При;
при;
при.

Пример 6.Решить уравнения: а) ; б) ; в) ; г) .
Решения:

А) I этап.
. Поэтому:
.

Б) I этап.
Поэтому:

Имеем следующие числовые промежутки:

III этап.
На первом промежутке:
На втором промежутке:
На третьем промежутке: нет решений.
Итог:
Ответ:

Имеем следующие числовые промежутки:

III этап.
;
;
.
Ответ: .

Имеем два полуинтервала:

Ответ: .

Пример 7. Решить системы уравнений:
а) б) в) г)

1) получаем решений нет;
2) получаем.
Вывод: и теперь из первого уравнения получаем.
Ответ: .

Расстояние между точками и это, согласно новой системе отсчета, расстояние между точками и, т.е.

Пример 8. Решить уравнения: а) б) в) г) д) .

Тогда.
Ответ: решений нет.

В) Перепишем уравнение в виде. Поэтому искомое x лежит в три раза ближе к 3, чем к 2:

=> нет решений, так как x всегда ближе к 2, чем к 3;
«на глазок», ;
=> «на глазок», .
Ответ: .

Нет решений;
(соответствует рассматриваемому полуинтервалу);
нет решений.
Ответ: .

Д) Начнем с применения метода интервалов:

Пример 9. Решить уравнения: а) б) в) г) .

Решения:

А) Левая часть уравнения неотрицательна при любых x, а в правой части - отрицательное число.
Ответ: решений нет.

Пример 10. Решить уравнения: а)
б) в) .

Решения:

Контрольные задания к §1.
1) Решите, пользуясь определением модуля числа:
а) б) в) г) д) е) ж) з) и) к) .

2)Решите «стандартные» уравнения:
а) б) в) г) д) е) ж) з) и) .

3) Решите методом интервалов:
а) б) ; в) г) д) е) ж) з) и) к) л) м) н) о) п) р) с) т) у) ф) х) ч)

4)Решите рациональным способом:
а) б) в) г) д) е) ж) з) и) к) л) м) н)

5)Решите системы уравнений:
а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) р)

Определение модуля n Модулем (абсолютной величиной) действительного числа х, т. е. | x|, называется само это число, если оно неотрицательное, и это число, взятое с противоположным знаком, если оно отрицательное

1. Свойства модуля 1. | а b | = | а | | b | для любых чисел а и b 2. | |= 3. при в ≠ 0 | а |2= а 2 для любого числа а

n n 2. Простейшим из уравнений, содержащих модули, является уравнение вида | f(x) | = a, где, а≥ 0. Данное уравнение равносильно совокупности уравнений. [ Если а

n n n Более сложными являются уравнения вида | f(x) | = g(x), где f(x), g(x) – некоторые функции действительного переменного х. 1) При g(x) 0 исходное уравнение равносильно совокупности Γ f(x) = g(x), Lf(x) = -g(x).

Пример 2. Решить уравнение | 1 – 2 x | = 3 x - 2 n Решение: Заметим, что Зх 2≥ 0, т. е. х ≥ или х є (; +∞) Нa множестве х є (; + ∞) заданное уравнение равносильно совокупности двух уравнений: 1) 1 -2 х=Зх-2 X 1 = 2)1 2 х= (Зх 2) X 2 = 1 n Поскольку

n n Теперь рассмотрим уравнения вида | а 1 х – в 1|+ | а 2 х – в 2 | + … + | аnх – вn | = ах + в, где а 1, а 2, а 3, … , аn, в 1, в 2, в 3 некоторые числа принадлежащие R, х действительная переменная строится по следующей схеме. Область допустимых значений переменной заданного уравнения разбивается на множества, на каждом из которых знаки подмодульных выражений постоянны. Нa каждом таком множестве исходное уравнение заменяется (с учётом знаков подмодульных выражений) эквивалентным ему уравнением, не содержащим абсолютных величин. Объединение решений полученной таким образом совокупности уравнении является решением заданного уравнения.

Пример 3. Решить уравнение | 2 х+5 | | 3 х | = 0, 5 n n n Решение. Область допустимых значений переменной вся числовая ось. Найдём точки, в которых подмодульные выражения равны 0: 2 х+5=0, т. е. х1= 2, 5; 3 х=0, т. е. х2 = 3.

n n n n n Разобьём область допустимых значений полученными точками на множества (∞; 2, 5), (2, 5; 3), (3; +∞) Определим знаки подмодульных выражений на каждом из полученных множеств (они записаны в таблице 1) Таблица 1 (∞; 2, 5) (2, 5; 3) (З; + ∞) 2 х + 5 + + 3–х + + Таким образом, исходное уравнение | 2 x+5 | | 3 х | =0, 5 равносильно совокупности уравнений: 1) х

n 2) при 2, 5 ≤ х

3. Теперь рассмотрим некоторые утверждения, применение которых позволяет значительно упростить решение уравнений с модулями. n n n Утверждение 1. Равенство | а+в | = | а | + | в | является верным, если ав ≥ 0. Доказательство. Действительно, после возведения обеих частей данного равенства в квадрат, получим, | а+в |2 = |a|2 + 2|ав | + |в|2 a 2 + 2 ав + в 2 = a 2 + 2|ав |+ в 2 , откуда | ав | = ав А последнее равенство будет верным при ав ≥ 0. Утверждение 2. Равенство | а-в | = | а | + | в | является верным при ав ≤ 0. Доказательство. Для доказательства достаточно в равенстве | а+в | = | а | + | в | заменить в на -в, тогда а(-в) ≥ 0, откуда ав ≤ 0

n n Утверждение 3. Равенство | а | + | в | = а+в выполняется при а≥ 0 и в ≥ 0. Доказательство. Рассмотрев четыре случая а≥ 0 и в ≥ 0; а≥ 0 и в

Пример 4. Решить уравнение: | 2 х 2| = |х3 2 | + | 2 х х3 | n n n Решение: Так как |х3 2 | + | 2 х х3 | = |х3 2 + 2 х х3 |, то все корни уравнения находятся среди решений неравенства (х3 2)(2 х – х3)≥ 0 (утверждение 1). Решим это неравенство методом интервалов; х(х3 – 2)(х2 – 2)≥ 0 х(х3 – 2)(х +)≤ 0 + + + 0 х Ответ: [ ; 0] U [ ; ]

4. В иных примерах совсем не следует торопиться с раскрытием модулей, надо прежде всего рассмотреть выражение в целом Пример 7. Решить уравнение: n В «целом» произведение двух дробей может быть равна 1 только в трёх случаях: n а) если дроби взаимно обратны, т. е. х+1= х+2 и | х+1| = | х+2|, но это не возможно при любых х. n б) если каждая из них равна 1, то получим и. Из первого уравнения следует х+1>0 х > 1. Из второго уравнения получим х+2>0 х> 2. Общее решение: х> 1. в) если каждая из них равна 1, то получим и. Из первого уравнения следует х+1

n n n Из второго уравнения получим х+2

Введение

1. Абсолютная величина в курсе средней школы

1.1 Определения и основные теоремы

1.2 Геометрическая интерпритация понятия |a|

2. Методы решения уравнений и неравенств

2.1 Решение уравнений и неравенств с использованием определения абсолютной величины (модуля)

2.2 Метод решения при помощи зависимостей между числами а и в, их модулями и квадратами этих чисел

2.3 Метод интервалов

2.4 Графический метод

2.5 Метод последовательного раскрытия модуля

2.6 Виды уравнений и неравенств и их решение

3. Дополнительные способы решения уравнений и неравенств

3.1 решение уравнений и неравенств, содержащих модуль, с использованием тождеств

3.2 Решение уравнений содержащих модули неотрицательных выражений

3.3 Решение уравнений с использованием геометрической интерпретации

3.4 Решение уравнений переходом к следствию

3.5 Типовые задачи, содержащие переменную под знаком модуля

3.6 Советы учителей по последовательности изучения уравнений и неравенств с модулем в школьном курсе математики

4. Уравнения и неравенства с модулем в Едином Национальном Тестировании (ЕНТ)

Заключение

Список использованной литературы

Введение

Актуальность темы связана с тем, что модуль широко применяется в различных разделах школьного курса математики, физики и технических науках. Например, в теории приближенных вычислений применяется понятия абсолютной и относительной погрешностей приближенного числа, понятия вектора и его длины (модуля вектора) используется в геометрии и механике, в математическом анализе понятие модуля содержится в определениях пределах, ограниченной функции. Я считаю, что эта тема требует более глубокого исследования, так как она прослеживается в различных заданиях повышенной сложности, которые предлагают учащимся авторы дидактических материалов, в задачах математических олимпиад, заданий ЕНТ и экзаменов при поступлении в вузы.

В практике преподавания математики в средней школе понятие абсолютной величины числа (модуля) встречается неоднократно.

В 6 классе, в теме приближенных вычислений формируется понятие абсолютой величины числа, при уяснении абсолютной погрешности приближенного числа.

Во втором полугодии 6 класса вводится определение абсолютной величины числа (модуля) и с помощью этого понятия формулируются правила действий над рациональными числами.

В 8 классе при рассмотрении свойств арифметического квадратного корня находит свое новое приложение понятие абсолютной величины числа:

; , где и другие.

В 9 классе, при изучении предела последовательности учащиеся встречаются с выражениями вида:

Понятие абсолютной величины числа получает свое дальнейшее развитие в 10 классе при изучении предела функции, при исследовании функции на ограниченность, при иучении комплексных чисел.

В 11 классее в теме «Степень с рациональным показателем» рассматриваются свойства корней n -й степени, где также используется понятие абсолютной велечины числа; так,например,

Таким образом, во всех классах, в соответствии с учебной программой, следует включать и рассматривать упражнения, содержащие знак абсолютной величины числа.

В 6 классе можно решать уравнения вида:

В 7 классе имеется вожможностьрссматривать решешие уравнений вида: и т.п., систем уравнений вида:

А так же пострение графиков функций: ; ; и др.

В 8 классе понятия абсолютной величины распространяются на квадратные уравнения, график квадратного трехчлена и др. можно решать уравненияя вида:; ;

Новизна дипломной работы : решили все уравнения и неравенства с моулем, встречающиеся в тестовых заданиях ЕНТ и рассмотрели основные ошибки, допускаемые учащимися при их решении.

Цель проведения нашего исследования – сделать анализ учебно-методического материала, выявить все методы решения уравнений и неравенств с модулем и объединить их в данной работе.

Для достижения поставленной необходимо решить следующие задачи :

Изучить основные теоремы и определения;

Описать основные методы решения уравнений и неравенств с модулем;

Выявить нестандартные методы решения уравнений и неравенств с модулем.

Объект исследования: процесс обучения уравнениям и неравенствам в школе.

Предмет исследования: методы решения уравнений и неравенств, содержащие знак модуля, в школьном курсе математики.

Практическая значимость дипломной работы состоит в том, что в данной дипломной предтавлены все методы и приемы решения уравнений и неравенств, которые можно использовать в школьном курсе математики.

Основными методами исследовани я в дипломной работе являются:

аналитический,

сравнительный,

изучение монографических публикаций и статей,

конкретно-исторический,

метод обобщения.

Данный диплом основан на следующих работах: «Абсолютная величина» Гайдуков И.И., «Уравнения и неравенства с модулями и методика их решения» Севрюков П.Ф., Смоляков А.Н., «Алгебра и начала анализа. Уравнения и неравенства 10 - 11кл» Олехник, Потапов, Пасиченко.

В первой главе рассматривается теоретическая сторона проблемы, основные теоремы и понятия, необходимые для дальнейшего исследования данной темы. уравнение задача неравенство

Во второй главе дипломной работы мы объединили методы решения уравнений и неравенств с модулем, которые входят в школьную программу.

В третьей главе мы представили нестандартные приемы решения уравнений и неравенств содержащие модуль, изучаемых на дополнительных занятиях и используемых при решении олимпиадных задач. Так же здесь рассмотрены типовые задания на решение уравнений и неравенств и задания тестовых вариантов Единого Национального Тестирования (ЕНТ).

При решении уравнений, содержащих знак абсолютной величины, мы будем основываться на определении модуля числа и свойствах абсолютной величины числа.

1. Абсолютная величина в курсе средней школы

1.1 Определения и основные теоремы

Рассмотрим понятие абсолютной велечины числа, или, что то же самое, модуля числа для действительных чисел.

Определение 1.1.1 Абсолютной величиной (модулем) действительного числа а называется неотрицательное число, взятое из двух чиисел а или - а.

Абсолютную величину числа а обозначают |а | и читают «абсолютная величина числа а», или «модуль числа а».

Из определения следует:

Из определения следует, что для любого действительного числа а, ≥0.

Примеры 1.1.1:

;

Теорема 1.1.1 Противоположные числа имеют равные абсолютные величины, т.е. = .

В самом деле, по определению абсолютной величины, имеем:

Следовательно,

1.2 Геометрическая интерпритация понятия

Известно, что каждому действительному числу можно поставить в соответствие точку числовой прямой, тогда эта точка будет геометрическим изображеннием данного действительного числа. Каждой точке числовой прямой соответствует ее расстояние от начала отсчета, иии длина отрезка, начало которого в точке начала отсчета, а конец – в данной точке.это расстояние, или длина отрезка, рассматривается всегда как величина неотрицательная.

Вместе с этим каждой точке числовой прямой можно поставить в соответсствие направленный отрезок(вектор), который характерезуется длинной и направлением.

Множеству действительных чисел соответствует множество точек ориентированной прямой, т.е. такой прямой на которой, кроме начала отсчета и маштаба, установлено положительное направление.

Тогда можно считать, что геометрической интерпритацией действительного числа служит вектор, выходящий из начала отсчета и имеющий конец в точке, изображающий данное число. Длина этого вектора будет геометрической интерпритацией абсолютной величины данного действительного числа.

Геометрическое толкование смысла наглядно потверждает, что = .

Примеры 1.2.1:

Если = 5, то а 1 =5 и а 2 =-5, или а = ±5.

Следовательно, данному равенству удовлетворяют два числа, которым на числовой прямой сответсвует две точки.

Если ˃10, то

Откуда а ˃10 и а ˂ -10, или

Следовательно, данному нераввенству удовлетворяет множество чисел двух интервалов: (-∞;-10) и (10;∞), а на числовой прямой – два промежутка соответствующие этим интервалам.

Перевод алгебраической задачи на геометрический язык – удобный и мощный метод решения задач. В качестве еще одного примера разберем блок задач олимпиады:

Пример 1.2.2:

Дана функция: .

Решение: Построим график функции . Для этого заметим, что , а тогда мы можем сначала построить график функции , и затем отразить его относительно оси координат. Преобразуем выражение, задающее функцию :

Поскольку данная система определяет верхнюю полуокружность радиуса 2 с центром в точке , график исходной функции представляет собой объединение полуокружностей указанных на рисунке.

Теперь решение задач не представляет труда:

с) При решений нет, при уравнение имеет три решения, при – четыре решения, при – два решения.

b ) Неравенство выполнено при всех из отрезка .

a ) корень уравнения есть абцисса точки пересечения прямой с графиком ффункции . Найдем ее геометрически: заштрихованный на рисунке прямоугольный треугольник является равнобедренный(угловой коэффицент прямой равен -1), его гипотенуза есть радиус окружности, ее длина 2. Тогда длина катета, лежащего на оси абсцисс есть , а искомая абсцисса равна .

Геомет рический смысл модуля разности величин - это расстояние между ними. Например, геометрический смысл выражения |х–а | -длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.

Пример 1.2.3: Решим уравнение |х–1|+|х–2|=1 с использованием геометрической интерпретации модуля.

Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок .

Ответ : х 

Пример 1.2.4: Решим уравнение |х – 1| - |х – 2|=1 1 с использованием геометрической интерпретации модуля.

Будем рассуждать аналогично предыдущему примеру, при этом получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Следовательно решением данного уравнения будет являтся не отрезок, заключенный между точками 1 и 2, а луч, выходящий из точки 2, и направленный в положительном направлении оси ОХ.

Ответ: х }