บทเรียนคณิตศาสตร์: ทำไมคุณหารด้วยศูนย์ไม่ได้ วิธีการแก้ปัญหาขีดจำกัด ความไม่แน่นอน ลำดับการเติบโตของฟังก์ชัน วิธีการเปลี่ยนอนันต์หารด้วยตัวเลข

หลายคนมักตั้งคำถามว่าทำไมการหารด้วยศูนย์ถึงใช้ไม่ได้? ในบทความนี้ เราจะพูดถึงรายละเอียดอย่างมากว่ากฎนี้มาจากไหน รวมถึงการดำเนินการใดที่สามารถทำได้โดยมีค่าศูนย์

ติดต่อกับ

ศูนย์สามารถเรียกได้ว่าเป็นตัวเลขที่น่าสนใจที่สุดตัวหนึ่ง ตัวเลขนี้ไม่มีความหมายมันหมายถึงความว่างเปล่าในความหมายที่แท้จริงของคำ อย่างไรก็ตาม หากคุณใส่ศูนย์ข้างตัวเลขใดๆ ค่าของตัวเลขนี้จะเพิ่มขึ้นหลายเท่า

ตัวเลขนั้นลึกลับมากในตัวเอง มันถูกใช้โดยคนมายาโบราณ ในมายา ศูนย์หมายถึง "จุดเริ่มต้น" และการนับถอยหลังของวันตามปฏิทินก็เริ่มจากศูนย์เช่นกัน

ข้อเท็จจริงที่น่าสนใจมากคือเครื่องหมายศูนย์และเครื่องหมายความไม่แน่นอนมีความคล้ายคลึงกันระหว่างทั้งสอง ด้วยเหตุนี้ มายาจึงต้องการแสดงให้เห็นว่า 0 เป็นเครื่องหมายเดียวกันกับความไม่แน่นอน ในยุโรปการกำหนดศูนย์ปรากฏขึ้นค่อนข้างเร็ว

นอกจากนี้ หลายคนทราบดีถึงการแบนที่เกี่ยวข้องกับศูนย์ ใครๆก็ว่า คุณไม่สามารถหารด้วยศูนย์... นี่คือสิ่งที่ครูพูดที่โรงเรียน และเด็กๆ มักจะเชื่อคำพูดของพวกเขา โดยปกติแล้ว เด็กไม่สนใจที่จะรู้เรื่องนี้ หรือพวกเขารู้ว่าจะเกิดอะไรขึ้นหากหลังจากได้ยินข้อห้ามสำคัญๆ แล้ว พวกเขาถามทันทีว่า "ทำไมคุณหารด้วยศูนย์ไม่ได้" แต่เมื่ออายุมากขึ้น ความสนใจก็ตื่นขึ้น และฉันต้องการทราบข้อมูลเพิ่มเติมเกี่ยวกับสาเหตุของการห้ามดังกล่าว อย่างไรก็ตาม มีหลักฐานที่สมเหตุสมผล

การดำเนินการเป็นศูนย์

ขั้นแรก คุณต้องกำหนดว่าการดำเนินการใดที่สามารถทำได้โดยมีค่าศูนย์ มีอยู่ การกระทำหลายประเภท:

• ส่วนที่เพิ่มเข้าไป;
• การคูณ;
• การลบ;
• กอง (ศูนย์ตามจำนวน);
• การยกกำลัง

สำคัญ!หากคุณบวกศูนย์ในตัวเลขใดๆ ระหว่างการบวก ตัวเลขนี้จะยังคงเหมือนเดิมและจะไม่เปลี่ยนค่าตัวเลข เช่นเดียวกันจะเกิดขึ้นถ้าศูนย์ถูกลบออกจากจำนวนใด ๆ

ด้วยการคูณและการหาร สิ่งต่าง ๆ แตกต่างกันเล็กน้อย ถ้า คูณจำนวนใด ๆ ด้วยศูนย์จากนั้นผลิตภัณฑ์จะกลายเป็นศูนย์เช่นกัน

ลองพิจารณาตัวอย่าง:

ลองเขียนสิ่งนี้เป็นส่วนเสริม:

มีเลขศูนย์เพิ่มมาทั้งหมด 5 ตัว ปรากฎว่า

ลองคูณหนึ่งด้วยศูนย์กัน... ผลลัพธ์ก็จะเป็นศูนย์เช่นกัน

ศูนย์สามารถหารด้วยจำนวนอื่นที่ไม่เท่ากับมันได้ ในกรณีนี้จะกลายเป็นค่าที่จะเป็นศูนย์ กฎเดียวกันนี้ใช้กับตัวเลขติดลบ ถ้าศูนย์หารด้วยจำนวนลบ คุณจะได้ศูนย์

คุณสามารถสร้างตัวเลขใดก็ได้ ถึงศูนย์องศา... ในกรณีนี้จะกลายเป็น 1 สิ่งสำคัญคือต้องจำไว้ว่านิพจน์ "ศูนย์ถึงศูนย์" นั้นไม่มีความหมายอย่างแน่นอน หากคุณพยายามเพิ่มศูนย์ให้เป็นกำลังใดๆ คุณจะได้ศูนย์ ตัวอย่าง:

โดยใช้กฎการคูณ เราได้ 0

เป็นไปได้ไหมที่จะหารด้วยศูนย์

ทีนี้มาถึงคำถามหลัก คุณหารด้วยศูนย์ได้ไหมโดยทั่วไป? และเหตุใดจึงไม่สามารถหารตัวเลขด้วยศูนย์ได้ เนื่องจากการกระทำอื่นๆ ทั้งหมดที่มีค่าศูนย์นั้นค่อนข้างมีอยู่จริงและถูกนำไปใช้ เพื่อตอบคำถามนี้ เราต้องหันไปหาคณิตศาสตร์ที่สูงขึ้น

เริ่มจากคำจำกัดความของแนวคิดก่อนว่าศูนย์คืออะไร? ครูโรงเรียนบอกว่าศูนย์ไม่มีอะไร ความว่างเปล่า นั่นคือเมื่อคุณบอกว่าคุณมี 0 ปากกา หมายความว่าคุณไม่มีปากกาเลย

ในวิชาคณิตศาสตร์ชั้นสูง แนวคิดของ "ศูนย์" นั้นกว้างกว่า ไม่ได้หมายถึงความว่างเปล่าเลย ศูนย์นี้เรียกว่าความไม่แน่นอน เพราะหากคุณค้นคว้าเพียงเล็กน้อย ปรากฎว่าเมื่อศูนย์ถูกหารด้วยศูนย์ เราสามารถลงเอยด้วยจำนวนอื่นๆ ซึ่งอาจไม่จำเป็นต้องเป็นศูนย์ก็ได้

คุณรู้หรือไม่ว่าการคำนวณทางคณิตศาสตร์อย่างง่ายที่คุณเรียนในโรงเรียนนั้นไม่เท่าเทียมกัน? การกระทำพื้นฐานที่สุดคือ การบวกและการคูณ.

สำหรับนักคณิตศาสตร์ ไม่มีคำว่า "" และ "การลบ" สมมติว่า: ถ้าคุณลบสามจากห้า มันจะเป็นสอง นี่คือลักษณะของการลบ อย่างไรก็ตาม นักคณิตศาสตร์จะเขียนแบบนี้:

ดังนั้น ปรากฎว่าความแตกต่างที่ไม่รู้จักคือจำนวนหนึ่งที่ต้องเพิ่มเป็น 3 เพื่อให้ได้ 5 นั่นคือคุณไม่จำเป็นต้องลบอะไรเลย คุณเพียงแค่ต้องหาจำนวนที่เหมาะสม กฎนี้ใช้กับการเพิ่ม

สิ่งต่าง ๆ เล็กน้อยด้วย กฎของการคูณและการหารเป็นที่ทราบกันดีว่าการคูณด้วยศูนย์ทำให้เกิดผลลัพธ์เป็นศูนย์ ตัวอย่างเช่น หาก 3: 0 = x ดังนั้นหากคุณพลิกบันทึก คุณจะได้ 3 * x = 0 และจำนวนที่คูณด้วย 0 จะให้ศูนย์ในผลคูณ ปรากฎว่าไม่มีตัวเลขที่จะให้ในผลิตภัณฑ์ที่มีค่าศูนย์ใด ๆ ที่ไม่ใช่ศูนย์ ซึ่งหมายความว่าการหารด้วยศูนย์ไม่มีความหมาย นั่นคือ มันเข้ากับกฎของเรา

แต่จะเกิดอะไรขึ้นถ้าคุณพยายามหารศูนย์ด้วยตัวเอง? ลองหา x จำนวนอนันต์มาเป็น x สมการคือ 0 * x = 0 ก็แก้ได้

หากเราพยายามหาศูนย์แทนที่จะเป็น x เราก็จะได้ 0: 0 = 0 มันจะดูเหมือนตรรกะ? แต่ถ้าเราลองเอาตัวเลขอื่นแทน x เช่น 1 เราก็จะได้ 0: 0 = 1 สถานการณ์เดียวกันจะเป็นถ้าคุณใช้หมายเลขอื่นและ แทนในสมการ.

ในกรณีนี้ ปรากฎว่าเราเอาเลขอื่นเป็นตัวประกอบก็ได้ ผลลัพธ์จะเป็นตัวเลขที่แตกต่างกันมากมายนับไม่ถ้วน บางครั้งการหารด้วย 0 ในวิชาคณิตศาสตร์ที่สูงกว่าก็สมเหตุสมผล แต่โดยปกติแล้วเงื่อนไขบางอย่างจะปรากฏขึ้น ทำให้เราสามารถเลือกตัวเลขที่เหมาะสมได้หนึ่งจำนวน การดำเนินการนี้เรียกว่า "การเปิดเผยความไม่แน่นอน" ในเลขคณิตธรรมดา การหารด้วยศูนย์จะสูญเสียความหมายไปอีกครั้ง เนื่องจากเราไม่สามารถเลือกตัวเลขใดจำนวนหนึ่งจากเซตได้

สำคัญ!ศูนย์ไม่สามารถหารด้วยศูนย์ได้

ศูนย์และอนันต์

อินฟินิตี้เป็นเรื่องธรรมดามากในวิชาคณิตศาสตร์ชั้นสูง เนื่องจากมันไม่สำคัญสำหรับเด็กนักเรียนที่จะรู้ว่ายังมีการดำเนินการทางคณิตศาสตร์ที่ไม่มีที่สิ้นสุด ครูจึงไม่สามารถอธิบายให้เด็กฟังได้ว่าทำไมจึงเป็นไปไม่ได้ที่จะหารด้วยศูนย์

นักเรียนเริ่มเรียนรู้ความลับทางคณิตศาสตร์ขั้นพื้นฐานเฉพาะในปีแรกของสถาบัน คณิตศาสตร์ชั้นสูงทำให้เกิดปัญหามากมายที่ไม่มีทางแก้ไข ปัญหาที่มีชื่อเสียงที่สุดคือปัญหาที่ไม่มีที่สิ้นสุด แก้ได้ด้วย การวิเคราะห์ทางคณิตศาสตร์

สมัครอินฟินิตี้ก็ได้ การคำนวณทางคณิตศาสตร์เบื้องต้น:บวกคูณด้วยจำนวน โดยปกติแล้ว การลบและการหารก็ใช้เช่นกัน แต่ในท้ายที่สุด พวกมันยังคงใช้การดำเนินการง่ายๆ สองอย่าง

แต่จะเกิดอะไรขึ้น ถ้าคุณลอง:

• อินฟินิตี้คูณศูนย์ ในทางทฤษฎี ถ้าเราพยายามคูณจำนวนใดๆ ด้วยศูนย์ เราก็จะได้ศูนย์ แต่อนันต์เป็นชุดของตัวเลขที่ไม่แน่นอน เนื่องจากเราไม่สามารถเลือกตัวเลขหนึ่งตัวจากชุดนี้ นิพจน์ ∞ * 0 จึงไม่มีวิธีแก้ไขและไม่มีความหมายอย่างยิ่ง
• ศูนย์หารด้วยอนันต์ เรื่องเดียวกันนี้เกิดขึ้นที่นี่เช่นเดียวกับข้างต้น เราไม่สามารถเลือกตัวเลขได้ ซึ่งหมายความว่าเราไม่รู้ว่าจะหารด้วยอะไร การแสดงออกไม่สมเหตุสมผล

สำคัญ!อินฟินิตี้ต่างจากความไม่แน่นอนเล็กน้อย! อินฟินิตี้เป็นความไม่แน่นอนชนิดหนึ่ง

ทีนี้ ลองหารอนันต์ด้วยศูนย์กัน ดูเหมือนว่าควรจะมีความไม่แน่นอน แต่ถ้าเราพยายามแทนที่การหารด้วยการคูณ เราจะได้คำตอบที่แน่ชัด

ตัวอย่างเช่น ∞ / 0 = ∞ * 1/0 = ∞ * ∞ = ∞

ออกมาเป็นแบบนี้ค่ะ ความขัดแย้งทางคณิตศาสตร์

เฉลยว่าทำไมหารด้วยศูนย์ไม่ได้

การทดลองทางความคิด พยายามหารด้วยศูนย์

บทสรุป

ดังนั้น ตอนนี้เรารู้แล้วว่าศูนย์เชื่อฟังการดำเนินการเกือบทั้งหมดที่ดำเนินการด้วย ยกเว้นการดำเนินการเดียว คุณไม่สามารถหารด้วยศูนย์เพียงเพราะผลลัพธ์คือความไม่แน่นอน นอกจากนี้เรายังได้เรียนรู้วิธีดำเนินการกับศูนย์และอนันต์ ความไม่แน่นอนจะเป็นผลมาจากการกระทำดังกล่าว

อนุพันธ์ของฟังก์ชันอยู่ไม่ไกลนัก และในกรณีของกฎของโลปิตาล ฟังก์ชันจะตกไปในทิศทางเดียวกับฟังก์ชันดั้งเดิมทุกประการ สถานการณ์นี้ช่วยในการเปิดเผยความไม่แน่นอนของแบบฟอร์ม 0/0 หรือ ∞ / ∞ และความไม่แน่นอนอื่นๆ ที่เกิดขึ้นเมื่อคำนวณ ขีดจำกัดอัตราส่วนของฟังก์ชันขนาดเล็กหรืออนันต์สองฟังก์ชัน การคำนวณนั้นง่ายขึ้นอย่างมากด้วยความช่วยเหลือของกฎนี้ (อันที่จริง กฎสองข้อและหมายเหตุสำหรับพวกเขา):

ตามสูตรข้างต้นแสดงให้เห็นว่า เมื่อคำนวณขีดจำกัดของอัตราส่วนของฟังก์ชันขนาดเล็กหรือขนาดใหญ่สองฟังก์ชัน ขีดจำกัดของอัตราส่วนของฟังก์ชันสองฟังก์ชันสามารถแทนที่ด้วยขีดจำกัดของอัตราส่วน อนุพันธ์และได้ผลลัพธ์ที่แน่นอน

ไปที่การกำหนดกฎเกณฑ์ของ L'Hôpital ที่แม่นยำยิ่งขึ้นกัน

กฎของโลปิตาลสำหรับกรณีจำกัดปริมาณน้อยๆ สองปริมาณ... ให้ฟังก์ชั่น ฉ(x) และ g(x เอ... และ ณ จุดนั้น เอ เออนุพันธ์ของฟังก์ชัน g(x) ไม่เท่ากับศูนย์ ( g"(x เอมีค่าเท่ากันและเท่ากับศูนย์:

.

กฎของโลปิตาลสำหรับกรณีการจำกัดปริมาณมากเป็นอนันต์ 2 รายการ... ให้ฟังก์ชั่น ฉ(x) และ g(x) มีอนุพันธ์ (เช่น อนุพันธ์) อยู่ในบริเวณใกล้เคียงของจุด เอ... และ ณ จุดนั้น เอพวกเขาอาจมีหรือไม่มีอนุพันธ์ นอกจากนี้ในบริเวณใกล้จุด เออนุพันธ์ของฟังก์ชัน g(x) ไม่เท่ากับศูนย์ ( g"(x) ≠ 0) และลิมิตของฟังก์ชันเหล่านี้เนื่องจาก x มีแนวโน้มที่ค่าของฟังก์ชันที่จุด เอมีค่าเท่ากันและเท่ากับอนันต์:

.

จากนั้นขีดจำกัดของอัตราส่วนของฟังก์ชันเหล่านี้จะเท่ากับขีดจำกัดของอัตราส่วนของอนุพันธ์:

กล่าวอีกนัยหนึ่ง สำหรับความไม่แน่นอนของรูปแบบ 0/0 หรือ ∞ / ∞ ลิมิตของอัตราส่วนของฟังก์ชันสองฟังก์ชันจะเท่ากับขีดจำกัดของอัตราส่วนของอนุพันธ์ ถ้าส่วนหลังมีอยู่ (จำกัด นั่นคือ เท่ากับ a จำนวนหนึ่งหรืออนันต์ นั่นคือ เท่ากับอนันต์)

หมายเหตุ.

1. กฎของ L'Hôpital ยังมีผลบังคับใช้เมื่อฟังก์ชันต่างๆ ฉ(x) และ g(x) ไม่ได้กำหนดไว้สำหรับ x = เอ.

2. ถ้าเมื่อคำนวณขีดจำกัดอัตราส่วนของอนุพันธ์ของฟังก์ชัน ฉ(x) และ g(x) อีกครั้งเรามาถึงความไม่แน่นอนของแบบฟอร์ม 0/0 หรือ ∞ / ∞ ดังนั้นกฎของ L'Hôpital ควรใช้หลายครั้ง (อย่างน้อยสองครั้ง)

3. กฎของโลปิตาลยังใช้ได้เมื่ออาร์กิวเมนต์ของฟังก์ชัน (x) มีแนวโน้มไม่เป็นจำนวนจำกัด เอและถึงอนันต์ ( x → ∞).

ความไม่แน่นอนของประเภทอื่นสามารถลดลงเป็นความไม่แน่นอนของประเภท 0/0 และ ∞ / ∞

การเปิดเผยความไม่แน่นอนของประเภท "ศูนย์หารด้วยศูนย์" และ "อนันต์หารด้วยอนันต์"

ตัวอย่างที่ 1

x= 2 ส่งผลให้เกิดความไม่แน่นอนของรูปแบบ 0/0 ดังนั้นอนุพันธ์ของแต่ละฟังก์ชันและเราได้รับ

อนุพันธ์ของพหุนามคำนวณในตัวเศษและในตัวส่วน - อนุพันธ์ของฟังก์ชันลอการิทึมเชิงซ้อน... ก่อนเครื่องหมายเท่ากับสุดท้าย ปกติ ขีดจำกัดแทนสองแทน x

ตัวอย่างที่ 2คำนวณขีดจำกัดอัตราส่วนของสองฟังก์ชันโดยใช้กฎของโลปิตาล:

สารละลาย. การแทนที่ค่าในฟังก์ชันที่กำหนด x

ตัวอย่างที่ 3คำนวณขีดจำกัดอัตราส่วนของสองฟังก์ชันโดยใช้กฎของโลปิตาล:

สารละลาย. การแทนที่ค่าในฟังก์ชันที่กำหนด x= 0 ส่งผลให้เกิดความไม่แน่นอนของรูปแบบ 0/0 ดังนั้นเราจึงคำนวณอนุพันธ์ของฟังก์ชันในตัวเศษและส่วนและรับ:

ตัวอย่างที่ 4คำนวณ

สารละลาย. การแทนที่ค่า x เท่ากับบวกอนันต์ลงในฟังก์ชันที่กำหนดทำให้เกิดความไม่แน่นอนของรูปแบบ ∞ / ∞ ดังนั้นเราจึงใช้กฎของโลปิตาล:

ความคิดเห็น ลองมาดูตัวอย่างที่ต้องใช้กฎของโลปิตาลสองครั้ง กล่าวคือ มาถึงจุดจำกัดอัตราส่วนของอนุพันธ์อันดับสอง เนื่องจากขีดจำกัดของอัตราส่วนของอนุพันธ์อันดับ 1 คือความไม่แน่นอนของรูปแบบ 0 /0 หรือ ∞ / ∞

การเปิดเผยความไม่แน่นอนของรูปแบบ "ศูนย์คูณอนันต์"

ตัวอย่างที่ 12คำนวณ

.

สารละลาย. เราได้รับ

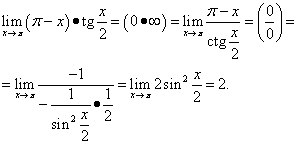
ตัวอย่างนี้ใช้เอกลักษณ์ตรีโกณมิติ

การเปิดเผยความไม่แน่นอนของประเภท "ศูนย์ยกกำลังศูนย์", "อนันต์ยกกำลังศูนย์" และ "หนึ่งต่อกำลังอนันต์"

ความไม่แน่นอนของแบบฟอร์ม หรือมักจะลดลงเป็นรูปแบบ 0/0 หรือ ∞ / ∞ โดยใช้ลอการิทึมของฟังก์ชันของแบบฟอร์ม

ในการคำนวณขีดจำกัดของนิพจน์ เราควรใช้เอกลักษณ์ลอการิทึม ซึ่งเป็นกรณีพิเศษที่เป็นคุณสมบัติของลอการิทึม .

การใช้เอกลักษณ์ลอการิทึมและคุณสมบัติความต่อเนื่องของฟังก์ชัน (เพื่อให้เกินเครื่องหมายจำกัด) ควรคำนวณขีดจำกัดดังนี้

แยกกัน คุณควรหาขีด จำกัด ของนิพจน์ในเลขชี้กำลังและ build อีในระดับที่พบ

ตัวอย่างที่ 13

สารละลาย. เราได้รับ

.

.

ตัวอย่างที่ 14คำนวณโดยใช้กฎของโลปิตาล

สารละลาย. เราได้รับ

เราคำนวณขีด จำกัด ของนิพจน์ในเลขชี้กำลัง

.

.

ตัวอย่างที่ 15คำนวณโดยใช้กฎของโลปิตาล

ถ้าจำนวนหารด้วยอนันต์ ผลหารมักจะเป็นศูนย์? เข้าไปข้างในก็ได้คำตอบที่ดีขึ้น

คำตอบจาก Olenka [มือใหม่]
ทั้งหมด 0
แคร็บบาร์
Oracle
(56636)
ไม่. ศูนย์ที่แน่นอน เนื่องจากตัวหารมีแนวโน้มเป็นอนันต์ ผลหารมักจะเป็นศูนย์ และถ้าเราไม่หารด้วยตัวเลขที่พุ่งไปที่อนันต์ แต่โดยอนันต์เอง (โดยที่มันแม่นยำกว่านั้นไม่ถือว่าเป็นตัวเลขอย่างเป็นทางการเลย แต่ถือเป็นสัญลักษณ์พิเศษที่เสริมการกำหนดตัวเลข) - ศูนย์อย่างแน่นอน .

คำตอบจาก ออกุส วลาดิเมียร์[คุรุ]
ศูนย์ แม้ว่าคุณจะหารหรือคูณมันด้วยตัวเลขใดๆ ก็ตาม มันก็ยังคงเป็นศูนย์!

คำตอบจาก 1 23 [คุรุ]
ถ้าอึบางอย่างมีแนวโน้มที่จะเป็นศูนย์ การคูณมันด้วยสิ่งที่จำกัด (จำนวนหรือฟังก์ชันจำกัด) จะไม่มีประโยชน์ patamu ที่ทุกอย่าง rna ana มีแนวโน้มที่จะเป็นศูนย์
แต่ถ้าคุณคูณมันด้วยสิ่งที่มุ่งมั่นเพื่อความไม่มีที่สิ้นสุด อาจมีทางเลือก

คำตอบจาก แคร็บบาร์[คุรุ]
เมื่อหารด้วยอนันต์ ตัวเลขใดๆ จะเป็นศูนย์ ศูนย์ที่แน่นอนไม่มี "ไปที่ศูนย์" แล้วคูณด้วยเลขอะไรก็ตาม ได้ศูนย์ และผลลัพธ์ของการหารศูนย์ด้วยจำนวนอื่นที่ไม่ใช่ศูนย์จะเป็นศูนย์ เฉพาะเมื่อหารศูนย์ด้วยศูนย์ ผลลัพธ์จะไม่ถูกกำหนด ว่าจำนวนใดจะเหมาะสมเป็นเชาวน์

วิธีการแก้ปัญหาขีดจำกัด ความไม่แน่นอน
ลำดับการเติบโตของฟังก์ชัน วิธีการเปลี่ยน

ตัวอย่างที่ 4

หาขีดจำกัด

นี่เป็นตัวอย่างที่ง่ายกว่าสำหรับโซลูชันที่ต้องทำด้วยตัวเอง ในตัวอย่างที่เสนอ มีความไม่แน่นอนอีกครั้ง (ของลำดับการเติบโตที่สูงกว่าราก)

ถ้า "x" มีแนวโน้มเป็น "ลบอนันต์"

ผีของ "ลบอนันต์" อยู่ในบทความนี้มานานแล้ว พิจารณาลิมิตของพหุนามที่ หลักการและวิธีการแก้ปัญหาจะเหมือนกันทุกประการกับในส่วนแรกของบทเรียน ยกเว้นความแตกต่างหลายประการ

พิจารณา 4 ชิปที่จำเป็นในการแก้ปัญหาในทางปฏิบัติ:

1) คำนวณวงเงิน

ค่าของลิมิตขึ้นอยู่กับเงื่อนไขเท่านั้น เนื่องจากมีลำดับการเติบโตสูงสุด ถ้าอย่างนั้น โมดูโลขนาดใหญ่ไม่สิ้นสุดตัวเลขติดลบยกกำลังคู่ในกรณีนี้ - ในสี่ เท่ากับ "บวกอินฟินิตี้":. ค่าคงที่ ("สอง") เชิงบวกนั่นเป็นเหตุผล:

2) คำนวณวงเงิน

ที่นี่อีกครั้งระดับอาวุโส สม่ำเสมอนั่นเป็นเหตุผล: . แต่อยู่หน้า "ลบ" ( เชิงลบค่าคงที่ -1) ดังนั้น:

3) คำนวณวงเงิน

ค่าขีดจำกัดขึ้นอยู่กับเท่านั้น ตามที่คุณจำได้จากโรงเรียน "ลบ" "กระโดด" จากระดับคี่ดังนั้น โมดูโลขนาดใหญ่ไม่สิ้นสุดเลขลบยกกำลังคี่เท่ากับ "ลบอนันต์" ในกรณีนี้:.
ค่าคงที่ ("สี่") เชิงบวก, วิธี:

4) คำนวณวงเงิน

เจ้าแรกในหมู่บ้านมาอีกแล้ว แปลกดีกรี ยิ่งกว่านั้น ในอ้อมอก เชิงลบคงที่ ซึ่งหมายความว่า: ดังนั้น:
.

ตัวอย่างที่ 5

หาขีดจำกัด

จากประเด็นข้างต้น เราสรุปได้ว่ามีความไม่แน่นอน ตัวเศษและตัวส่วนมีลำดับการเติบโตเหมือนกัน ซึ่งหมายความว่าในขีดจำกัด คุณจะได้จำนวนจำกัด มาหาคำตอบกันทิ้งลูกปลาทั้งหมด:

การแก้ปัญหาเป็นเรื่องเล็กน้อย:

ตัวอย่างที่ 6

หาขีดจำกัด

นี่คือตัวอย่างสำหรับโซลูชันที่ต้องทำด้วยตัวเอง กรอกคำตอบและคำตอบในตอนท้ายของบทช่วยสอน

และตอนนี้อาจเป็นกรณีที่ละเอียดอ่อนที่สุด:

ตัวอย่าง 7

หาขีดจำกัด

เมื่อพิจารณาจากเงื่อนไขชั้นนำ เราสรุปได้ว่ามีความไม่แน่นอน ตัวเศษมีลำดับการเติบโตที่สูงกว่าตัวส่วน ดังนั้นคุณสามารถพูดได้ทันทีว่าขีดจำกัดคืออนันต์ แต่อนันต์ใด บวก หรือ ลบ? เทคนิคเหมือนกัน - ในตัวเศษและส่วน เรากำจัดสิ่งเล็กน้อย:

เราตัดสินใจ:

หารตัวเศษและตัวส่วนด้วย

ตัวอย่าง 15

หาขีดจำกัด

นี่คือตัวอย่างสำหรับโซลูชันที่ต้องทำด้วยตัวเอง ตัวอย่างคร่าวๆของการจบบทเรียน

ตัวอย่างที่น่าสนใจอีกสองสามตัวอย่างเกี่ยวกับการแทนที่ตัวแปร:

ตัวอย่างที่ 16

หาขีดจำกัด

เมื่อแทนที่หน่วยในขีด จำกัด จะได้รับความไม่แน่นอน การแทนที่ตัวแปรนั้นชัดเจนอยู่แล้ว แต่ก่อนอื่น เราแปลงแทนเจนต์โดยใช้สูตร ที่จริงแล้วทำไมเราถึงต้องการแทนเจนต์?

สังเกตว่า ดังนั้น ถ้าไม่ชัดเจนทั้งหมดให้ดูค่าไซน์ใน ตารางตรีโกณมิติ... ดังนั้นเราจึงกำจัดตัวคูณออกทันที นอกจากนี้ เรายังได้รับความไม่แน่นอน 0: 0 ที่คุ้นเคยมากขึ้น คงจะดีถ้าขีดจำกัดของเรามีแนวโน้มเป็นศูนย์

มาแทนที่:

ถ้าอย่างนั้น

ภายใต้โคไซน์ เรามี "x" ซึ่งต้องแสดงผ่าน "te" ด้วย
จากการแทนที่เราแสดง:.

เราดำเนินการแก้ไขให้เสร็จสิ้น:

(1) เราทำการทดแทน

(2) ขยายวงเล็บใต้โคไซน์

(4) การจัด ขีด จำกัด แรกที่ยอดเยี่ยมคูณเทียมตัวเศษด้วย และส่วนกลับ.

การมอบหมายโซลูชันอิสระ:

ตัวอย่าง 17

หาขีดจำกัด

กรอกคำตอบและคำตอบในตอนท้ายของบทช่วยสอน

สิ่งเหล่านี้ไม่ใช่งานยากในชั้นเรียน ในทางปฏิบัติทุกอย่างอาจเลวร้ายลง และนอกเหนือจาก สูตรลด, คุณต้องใช้หลากหลาย สูตรตรีโกณมิติรวมไปถึงทริคอื่นๆ ในบทความ ขีดจำกัดที่ยาก ฉันได้แยกตัวอย่างจริงสองสามตัวอย่าง =)

ในวันหยุดนี้ เรามาชี้แจงสถานการณ์ด้วยความไม่แน่นอนในวงกว้างอีกครั้งหนึ่ง:

ขจัดความไม่แน่นอน "หนึ่งถึงระดับอนันต์"

ความไม่แน่นอนนี้ "ให้บริการ" ขีด จำกัด ที่ยอดเยี่ยมที่สองและในส่วนที่สองของบทเรียนนั้น เราได้ตรวจสอบตัวอย่างมาตรฐานของวิธีแก้ปัญหาอย่างละเอียด ซึ่งส่วนใหญ่แล้วจะพบในทางปฏิบัติ ตอนนี้รูปภาพกับผู้เข้าร่วมงานจะเสร็จสมบูรณ์ นอกจากนี้ งานสุดท้ายของบทเรียนจะทุ่มเทให้กับข้อ จำกัด - "เคล็ดลับ" ซึ่งดูเหมือนว่าจำเป็นต้องใช้ขีด จำกัด ที่ยอดเยี่ยมที่ 2 แม้ว่าจะไม่ได้อยู่ที่ ทุกกรณี

ข้อเสียของสูตรการทำงานสองสูตรของลิมิตที่น่าทึ่งที่ 2 คืออาร์กิวเมนต์ต้องมีแนวโน้มเป็น "บวกอนันต์" หรือเป็นศูนย์ แต่ถ้าอาร์กิวเมนต์มีแนวโน้มเป็นตัวเลขอื่นล่ะ

สูตรสากลเข้ามาช่วย (ซึ่งอันที่จริงเป็นผลมาจากขีด จำกัด ที่สองที่น่าทึ่ง):

ความไม่แน่นอนสามารถกำจัดได้โดยสูตร:

ที่ไหนสักแห่งเช่นอธิบายแล้วว่าวงเล็บเหลี่ยมหมายถึงอะไร ไม่มีอะไรพิเศษ วงเล็บก็เหมือนวงเล็บ มักใช้เพื่อทำให้สัญกรณ์ทางคณิตศาสตร์ชัดเจนขึ้น

มาเน้นประเด็นสำคัญของสูตรกัน:

1) มันคือ เกี่ยวกับความไม่แน่นอนเท่านั้น และไม่มีอื่นใด.

2) อาร์กิวเมนต์ "x" อาจมีแนวโน้มที่จะ มูลค่าตามอำเภอใจ(และไม่เพียงแต่เป็นศูนย์หรือ) โดยเฉพาะกับ "ลบอนันต์" หรือถึง ใด ๆจำนวนจำกัด

คุณสามารถใช้สูตรนี้เพื่อแก้ตัวอย่างทั้งหมดของบทเรียนได้ ขีดจำกัดที่ยอดเยี่ยมซึ่งเป็นของลิมิตอันน่าทึ่งที่ 2 ตัวอย่างเช่น ลองคำนวณขีดจำกัด:

ในกรณีนี้ และโดยสูตร:

จริงฉันไม่แนะนำให้คุณทำเช่นนี้ตามธรรมเนียมแล้วยังคงใช้การออกแบบ "ปกติ" ของโซลูชันหากสามารถใช้ได้ แต่ ใช้สูตรเช็คสะดวกมากตัวอย่าง "คลาสสิก" ที่ 2 ขีด จำกัด ที่น่าทึ่ง